Таблицы произведений элементов групп

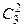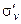Определенные выше шесть операций симметрии (E, C₃ , , σ_v, и 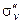) описывают все возможные операции симметрии хлористого метила. Его группа симметрии имеет порядок 6. Все эти операции показаны на рис. 2.1. Для того чтобы проверить, что они удовлетворяют групповым постулатам, составим таблицу произведений элементов группы. Если мы построим квадратную таблицу, строки и столбцы которой обозначены операциями группы, и заполним её произведениями соответствующих операций группы, то получим таблицу произведений. В качестве примера мы приводим табл.2.1, составленную для произвольных операций. Порядок произведения

Таблица 2.1. Таблица произведений для группы произвольных операций

	А	В	С	…
А	АА	АВ	АС	…
В	ВА	ВВ	ВС	…
С	СА	СВ	СС	…
…	…	…	…	…

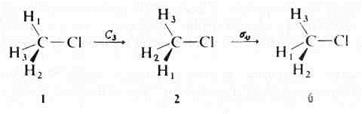
такой: первым выполняется элемент столбца, вторым – элемент строки. Таблица произведений элементов группы для операций симметрии СН₃Сl может быть получена с учётом рис. 2.1. Произведение двух операций определяется как последовательное применение двух операций, причём первой выполняется операция, стоящая справа. Необходимо отметить, что элементы симметрии всегда сохраняют свою первоначальную ориентацию, которая не изменяется при преобразовании молекулы. Например, выполнение операции σ_vC₃ начинается с поворота С₃, за которым следует отражение.

	(2.10)
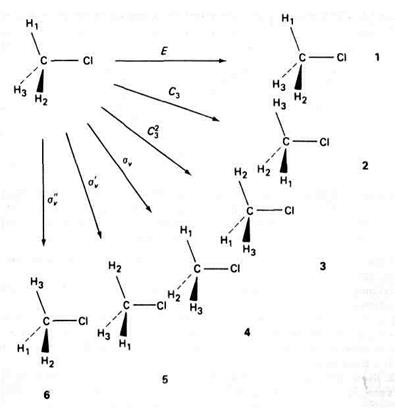Рис. 2.1. Операции симметрии хлористого метила.

Заметим, что после выполнения С₃ отражение σ_v производиться в плоскости Н₃ – С – Сl. Конечным результатом является конфигурация 6 на рис. 2.1. Это означает, что произведение σ_vC₃ эквивалентно :

(2.11)

Аналогично можно определить все другие бинарные произведения. Все произведения операции симметрии хлористого метила приведены в табл. 2.2. Необходимо отметить, что каждый элемент группы появляется в каждой строке и каждом столбце один и только один раз.

Таблицу 2.2. можно использовать для проверки того факта, что операции симметрии хлористого метила удовлетворяют групповым постулатам:

1. Композиция двух элементов группы даёт третий элемент, также являющийся элементом группы. Это следует из того, что все элементы в таблице произведений (все возможные бинарные произведения элементов) являются элементами группы.

2. Выполняется ассоциативный закон. Рассмотрим произвольное тройное произведение, скажем . Его можно сгруппировать двумя путями: или 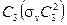. Результаты произведений следующие:

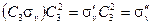(2.12а)

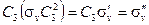(2.21б)

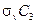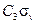Аналогичные результаты получаются для любого многократного произведения. Отметим, однако, что данная группа неабелева (коммутативный закон выполняется не для всех элементов). Например, равно , в то время как равно .

3. В группу можно включит элемент, коммутирующий с любым другим и оставляющий его неизменным. Это единичный элемент:

ЕА = АЕ = А

(2.13)

4.Элемент, обратный к каждому элементу группы, также является элементом группы. Например, из таблицы видно, что

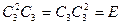(2.14)

Элементы 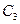и обратны по отношению друг к другу.

Таблица 2.2. Таблица произведений операций симметрии хлористого

метила (точечная группа С_3v)

	Е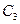
Е	Е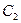
С3	С3		Е
		Е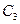
				Е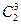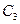
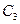					Е
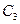						С

Аналогично можно определить все другие бинарные произведения. Все произведения операций симметрии хлористого метила приведены в табл. 2.2. Необходимо отметить, что каждый элемент группы появляется в каждой строке и каждом столбце таблицы один и только один раз.

Упражнение 2.3. Построить таблицы произведений операций симметрии молекул, указанных в предыдущем упражнении.

Таблицу 2.2 можно использовать для проверки того факта, что операции симметрии хлористого метила удовлетворяют групповым постулатам:

1. Композиция двух элементов группы даёт третий элемент, также являющийся элементом группы. Это следует из того, что все элементы в таблице произведений (все возможные бинарные произведения элементов) являются элементами группы.

2. Выполняется ассоциативный закон. Рассмотрим произвольное тройное произведение, скажем 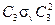. Его можно сгруппировать двумя путям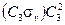и или 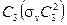. Результаты этих произведений следующие:

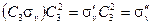	(2.12а)
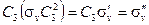	(2.12б)

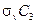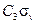Аналогичные результаты получаются для любого многократного произведения. Отметим, однако, что данная группа неабелева (коммутативный закон выполняется не для всех элементов). Например, равно , в то время как равно .

3. В группу можно включить элемент, коммутирующий с любым элементом и оставляющий его неизменным. Это единичный элемент:

ЕА=АЕ=А

(2.13)

4. Элемент, обратный к каждому элементу группы, также является элементом группы. Например, из таблицы видно, что

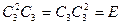(2.14)

Элементы 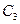и обратны по отношению друг к другу. Отражения в плоскости симметрии являются обратными самим себе.

Итак, операции симметрии хлористого метила удовлетворяют групповым постулатам и поэтому определяют математическую группу. Аналогичная ситуация имеет место для операций симметрии, описывающих любую систему. Группы, определяющие симметрию одного объекта, называются точечными группами, так как элементы симметрии такого объекта пересекаются в некоторой точке. Все свойства произвольной математической группы присущи и группе симметрии.

Генераторы и подгруппы

Рассмотрим два элемента, С₃ и σ_v , из группы симметрии хлористого метила (эта группа обозначается как С_3v и является точечной группой) и найдём результаты всевозможных произведений их друг с другом и на себя. Из таблицы произведений (табл. 2.2) следует, что

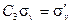	(2.15а)
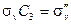	(2.15б)
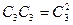	(2.15в)
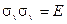	(2.15г)

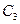Другими словами, с помощью этих двух элементов можно получить все другие элементы в данной точечной группе. Говорят, что эти два элемента являются генераторами группы. Они не единственны. Вместо С₃ можно использовать и вместо – или . Однако вся группа не может быть порождена только элементами и .

Упражнение 2.4. Генераторами группы симметрии дихлорметана являются С₂ и σ_v; для трёхфтористого бора это С₃, ось С₂ , перпендикулярная С₃, плоскость симметрии σ_h, перпендикулярная С₃; для циклогексана в форме кресла – С₃, ось С₂, перпендикулярная С₃, и плоскость симметрии σ_d, содержащая С₃ и делящая пополам пару осей С₂. Проверить, что все указанные элементы симметрии являются генераторами групп симметрии соответствующих молекул.

Степени С₃ порождают так называемую циклическую подгруппу точечной группы С_3v. Подгруппа – это множество элементов группы, удовлетворяющее групповым постулатам. Элементы 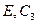и образуют группу (точечную группу С₃). Эта группа содержится в С_3v, и поэтому является её подгруппой. Три другие подгруппы точечной группы С_3v – 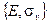, 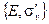и 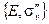– полностью эквивалентны друг другу. Говорят, что группа является циклической, если она содержит только степени одного и того же элемента, включая и единичный элемент как некоторую степень указанного элемента. Группа, содержащая только степени одного элемента, является циклической, если только она не бесконечного порядка. Все циклические группы абелевы.

Произведения групп

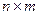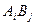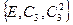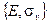Одной из операций, которые могут быть определены для групп, является произведение независимых групп. Если группа А состоит из n элементов {А₁, А₂ . . ., А_n} и группа В – из m элементов {В₁, В₂ . . . В_n}, то их произведение содержит элементов вида . Например, произведения групп и является

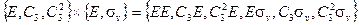=	(2.16)
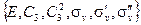=	(2.16а)

Другими словами, группа может быть порождена произведениями своих независимых циклических подгрупп. Все возможные точечные группы симметрии могут быть построены как произведения двух или трёх циклических подгрупп, причём каждая подгруппа порождается различными генераторами группы. Тогда очевидно, что порядок подгруппы должен быть целым делителем порядка группы (т. е. группа порядка 6 может иметь подгруппы 2 и 3, а группа порядка 8 может иметь подгруппы порядка 2 и 4 и т. д.). Заметим, что произведение подгрупп 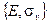и 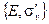не порождает группы:

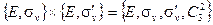(2.17)

Из табл. 2.2 непосредственно следует, что 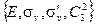не образует группы. Причина этого заключается в том, что 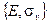и 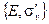не являются независимыми группами. Элементы и имеют различный смысл только тогда, когда они относятся к системе, задающей им определённое направление.

В формуле (2.16) группа 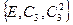умножается справа на группу 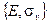. Если порядок сомножителей в произведении заменён на обратный, то

=

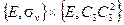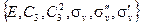(2.18)

Получаются те же самые элементы, но расположение их другое. Это произошло потому, что 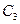и не коммутируют с . В силу этого определяют два типа произведения групп. Произведения групп с некоммутирующими элементами типа (2.16) и (2.18) будем называть полупрямыми произведениями (обозначаются символом 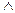). Произведения групп, для которых все элементы одной группы коммутируют со всеми элементами другой группы, будем называть прямыми произведениями (обозначаются символом 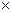). Итак, если мы обозначим группу 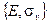как С_s, то

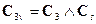(2.19)

Порядок сомножителей в полупрямом произведении имеет значение. Рассмотрим произведения подгруппы С₃сσ_v. Если подгруппа умножается справа на σ_v, то

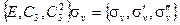(2.20а)

Если умножение производится слева, то

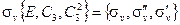(2.20б)

То есть получаются одни и те же множества элементов (такие множества называют смежными классами). Говорят, что подгруппа С₃ инвариантна по отношению к . Очевидно, что она инвариантна к Е (поскольку Е коммутирует со всеми элементами и оставляет их неизменными). Итак, подгруппа С₃ инвариантна по отношению к элементам подгруппы С_s. Рассмотрим правые и левые произведения подгруппы С_s с элементом С₃:

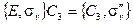	(2.21а)
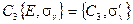	(2.21б)

Результаты получились разные. Аналогичная ситуация имеет место и в случае умножения на . Следовательно, подгруппа С_s не инвариантна по отношению к элементам подгруппы С₃. Такая ситуация всегда имеет место для полупрямых произведений. Только одна подгруппа будет инвариантна по отношению к элементам другой. По определению в полупрямых произведениях инвариантная подгруппа записывается первой, как в формуле (2.19). Так как в прямом произведении все элементы одной подгруппы коммутируют со всеми элементами другой, то порядок записи сомножителей в прямом произведении несущественен. Это приводит к таким коммутационным соотношениям:

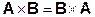	(2.22а)
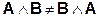	(2.22б)

Фактически, если левая часть (2.22б) имеет смысл, то правая часть неопределённа.

Существует также ещё один тип произведения, так называемое слабое прямое произведение. В слабом прямом произведении ни одна подгруппа не коммутирует со всеми элементами другой. В данном пособии этот тип произведения не рассматривается.

Упражнение 2.5^*.

а) Найти подгруппы групп симметрии из предыдущих трёх задач.

б) Установить соотношения для прямого и полупрямого произведений.

Смежные классы

Каждая подгруппа связана с одним или более смежными классами. Смежный класс определяется как произведение подгруппы с одним из элементов группы, не принадлежащим подгруппе. Например, можно образовать смежные классы подгруппы 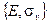точечной группы С_3v с элементам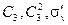и и . В результате получаем

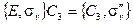	(2.23а)
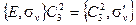	(2.23б)
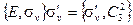	(2.23в)
	(2.23г)

Определённые этим соотношениями смежные классы называются правыми. Так же можно определить левые смежные классы, однако они аналогичны правым смежным классам, изменяется только их порядок. Например, если мы пренебрегаем порядком внутри класса, то

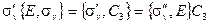(2.24)

Смежные классы обладают следующими четырьмя важными свойствами:

1. Каждый элемент группы принадлежит либо данной подгруппе, либо одному из элементов её смежных классов.

2. Пересечение подгруппы с любым из её смежных классов пусто.

3. Пересечение двух различных смежных классов одной и той же подгруппы пусто.

4. Каждый элемент группы содержится только в одном смежном классе.

Подобно построению группы как произведения подгрупп, порождаемых генераторами, она может быть построена из единственной подгруппы и её смежных классов.

2.8. Сопряжённые элементы и классы

Два элемента А и В называются сопряжёнными, если существует элемент R, такой, что

A = RBR-1

(2.25)

В такой записи А сопряжён с В относительно R. Аналогичное соотношение для В имеет вид

B = R-1AR

(2.26)

В такой записи В сопряжён с А относительно R^-1. Множество взаимно сопряжённых элементов в группе называется классом. Класс может содержать только один элемент (единичный элемент всегда образует класс) или несколько элементов. Сопряжённые элементы точечной группы С_3v можно найти с помощью таблицы произведений (табл. 2.2). Например, сопряжённый с относительно С₃ элемент

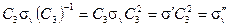(2.27)

По аналогии с таблицей произведений можно построить таблицу сопряжённых элементов. Для точечной группы С_3v все сопряжённые элементы приведены в табл. 2.3. каждый из столбцов С₃ и содержит только С₃ и . Поэтому эти два элемента составляют класс. Каждый из столбцов 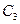и содержит только 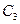и . Поэтому эти два элемента составляют класс. Каждый из трёх - столбцов содержит только три операции ; следовательно, элементы типа образуют класс. Элементы группы С_3v часто обозначают только классами как .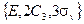

Упражнение 2.6. Определить классы для каждой из групп симметрии, рассмотренных в предыдущем упражнении.

Таблица 2.3 Таблица сопряжённых элементов точечной группы С_3v ^а)

R A	E	C3		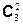		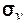	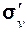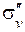A R-1
E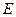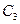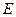

_______

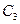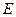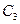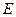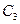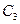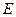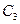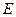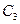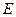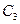а) Каждый элемент таблицы - тройное произведение вида RAR^-1, где элемент R взят из крайнего левого столбца, элемент А – из верхней строки и элемент R^-1 , обратный R – изкрайнего правого столбца.

Сопряжённые подгруппы определяются аналогичным образом. Если элементы { А₁, А₂, … А_n } образуют подгруппу некоторой группы и R – элемент группы, то множество { B₁, B₂, … B_n }, определяемое как

{ B1, B2, … , Bn } = R{ A1, A2, … , An }R-1

(2.28)

является сопряжённой подгруппой относительно элемента R. Сопряжённые подгруппы должны быть также подгруппами группы. Особый и важный случай сопряжённой подгруппы – это случай, когда подгруппа совпадает со своей сопряжённой подгруппой относительно любого элемента группы

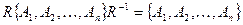для всех R

(2.29)

Такие подгруппы называются инвариантными подгруппами.

2.9. Отображения[2]

Часто бывает полезно представить элементы некоторой группы другими величинами, удовлетворяющими той же самой таблице произведений, что и заданная группа. Тогда говорят, что данная группа отображается в новую группу, причём каждый элемент в первоначальной группе имеет образ в новой. При этом совсем не обязательно, чтобы различные элементы в первоначальной группе имели различные образы в новой. Если различные элементы исходной группы имеют различные образы, то говорят, что группы изоморфны; в противном случае, они называются гомоморфными. В качестве примера рассмотрим отображения циклической точечной группы С₄,приведённые в табл. 2.4. Величина всех элементов в этих отображениях равна единице. Если в качестве группового произведения взять обычное умножение, то элементы каждого отображения образуют группу. Первая группа имеет порядок равный единице (содержит всего только один элемент), вторая – двум (два элемента), в то время как две последние группы, так же как и исходная группа, имеет порядок четыре. Так как в первом случае четыре элемента отображаются в один, то говорят, что имеет место 4-1– отображение. Во втором случае осуществляется 2-1– отображение. Оба эти отображения являются гомоморфизмами. В последних двух случаях осуществляется 1-1– отображения и обе группы изоморфны С₄.

Таблица 2.4. Отображения точечной группы С₄

С4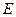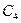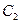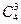
	1	1	1	1
	1	-1	1	-1
	1	i	-1	-i
	1	-i	-1	i

Представления

Рассмотрим снова молекулу хлористого метила в трёхмерной декартовой системе координат (рис. 2.2). Три атома водорода находятся в плоскости xy, причём Н₁ – на положительной полуоси x. Атомы углерода и хлора находятся на оси z. Все операции симметрии сводятся к взаимозамене атомов водорода в плоскости xy; следовательно, можно ограничится рассмотрением только этой плоскости. Проведём к каждому из атомов водорода единичные векторы из начала координат в плоскости xy (рис. 2.3). ( Числа на рисунке – x- и y- компоненты каждого вектора). Рассмотрим следующий набор двумерных унитарных матриц преобразования:

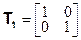(2.30а)

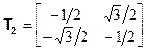(2.30б)

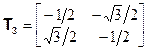(2.30в)

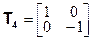(2.30г)

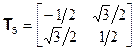(2.30д)

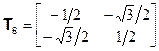(2.30е)

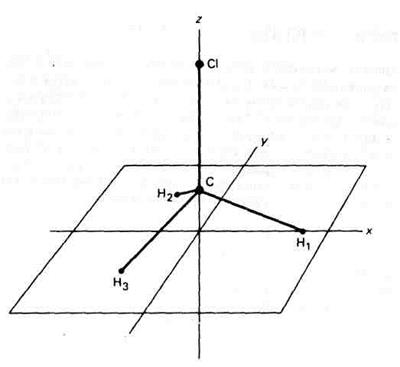Рис. 2.2. Молекула хлористого метила в трёхмерной декартовой системе координат

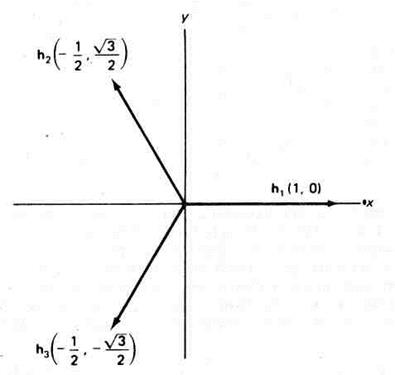Рис. 2.3. Проекция молекулы хлористого метила на плоскость xy с единичными векторами, проведёнными из начала координат к каждому атому водорода.

Отметим, что cos 120⁰ и cos 240⁰ равны 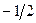, sin 120⁰ равен 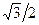и sin 240⁰ равен 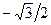. Поэтому (2.30б) и (2.30в) представляют собой двумерные матрицы поворотов на углы 120 и 240⁰ соответственно.

Эти матрицы преобразуют векторы на рис. 2.3 точно так же, как соответствующие операции симметрии преобразуют атомы водорода молекулы хлористого метила. Например, рассмотрим Т₅, соответствующую . Эта матрица действует на единичные векторы следующим образом:

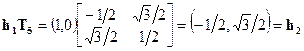(2.31а)

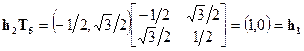(2.31б)

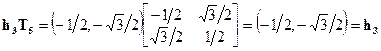(2.31в)

Из произведений матриц можно составить таблицу, полностью идентичную таблице произведений элементов точечной группы С_3v. Например, произведение Т₂Т₄ равно

Т2Т4 = 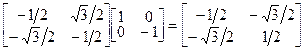= Т6

(2.32)

Матрица Т₂ соответствует С₃, Т₄ – и Т₆ – , таким образом, вспоминая контравариантное поведение операторов и ассоциированных с ними матриц, имеем

hiT2T4 = σvC3hi

(2.33)

Произведение матриц полностью аналогично произведению

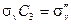(2.34)

Матрицы Т₁ – Т₆ образуют группу, изоморфную точечной группе С_3v. Если можно найти множество матриц, представляющее собой группу, которая имеет такую же таблицу произведений, что и данная группа, то говорят, эти матрицы порождают матричное представление (или просто представление) группы. Множество матриц Т₁ – Т₆ даёт представление группы С_3v.

Упражнение 2.7^*. Определить двумерные унитарные матрицы, представляющие операции дихлорметана.

Группа матриц, являющаяся представлением данной группы, не обязательно должна быть изоморфна последней. Матрицы не должны обладать определённой размерностью. Они могут быть одномерными (т.е. скалярами), двумерными, трёхмерными или иметь ещё большую размерность. Они могут быть действительными, комплексными или мнимыми. Единственное требование к ним заключается в том, что они должны быть гомоморфны рассматриваемой группе и удовлетворять таблице произведений группы. В действительности для данной группы существует бесконечное множество возможных представлений.

ГЛАВА III

Точечная симметрия