Уравнение бегущей волны. Фазовая скорость. Волновое уравнение

Бегущими волнаминазываются волны, ко­торые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности по­тока энергии.Этот вектор для упругих волн называется вектором Умова(по име­ни русского ученого Н. А. Умова (1846— 1915), решившего задачу о движении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, пере­носимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распро­странения волны.

Для вывода уравнения бегущей во­лны — зависимости смещения колеблю­щейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический ха­рактер, а ось х совпадает с направлением распространения волны (рис. 220). В дан­ном случае волновые поверхности перпен­дикулярны оси х, а так как все точки волновой поверхности колеблются одина­ково, то смещение x будет зависеть только от х и t, т. е. x=x(х, t).

На рис. 220 рассмотрим некоторую частицу среды В, находящуюся от источ­ника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х=0, описываются функцией x(0, t)=Аcoswt, то частица среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источ­ника на т, так как для прохождения во­лной расстояния х требуется время t=x/v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид

x(x,t)=Acosw(t-x/v), (154.1)

откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегу­щей волны.Если плоская волна распро­страняется в противоположном направлении, то

x(х, t)=A cosw(t+x/v).

В общем случае уравнение плоской волны,распространяющейся вдоль поло­жительного направления оси х в среде, не поглощающей энергию, имеет вид

x(x,t)=Acos[w(t -х/v)+j₀], (154.2)

где А=const — амплитуда волны,w— циклическая частота волны,j₀ — началь­ная фаза колебаний,определяемая в об­щем случае выбором начал отсчета х и t, [w(t-x/v)+j₀]—фаза плоской волны.

Для характеристики волн использует­ся волновое число

k=2p/l=2p/vT=w/v. (154.3) Учитывая (154.3), уравнению (154.2) можно придать вид

x(x,t)=Acos(wt-kх+j₀). (154.4)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком чле­на kx.

Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде

x(x,t)=Ae^i(wt-kx+j0),

где физический смысл имеет лишь дей­ствительная часть (см. § 140).

Предположим, что при волновом про­цессе фаза постоянна, т. е.

w(t-x/v)+j₀=const. (154.5) Продифференцировав выражение (154.5) и сократив на w, получим

dt-(1/v)dx=0, откуда

dx/dt=v. (154.6)

Следовательно, скорость v распростране­ния волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы во­лны, и ее называют фазовой скоростью.

Повторяя ход рассуждений для плоской волны, можно доказать, что урав­нение сферической волны— волны, волновые поверхности которой имеют вид кон­центрических сфер, записывается как

x(r,t)=A₀/rcos(wt-kr+j₀), (154.7)

где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не по­глощающей энергию, амплитуда колеба­ний не остается постоянной, а убывает с расстоянием по закону 1/r. Уравнение (154.7) справедливо лишь для r, значи­тельно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Из выражения (154.3) вытекает, что фазовая скорость

v=w/k. (154.8)

Если фазовая скорость волн в среде за­висит от их частоты, то это явление на­зывают дисперсией волн,а среда, в кото­рой наблюдается дисперсия волн, называ­ется диспергирующей средой.

Распространение волн в однородной изотропной среде в общем случае описы­вается волновым уравнением— диффе­ренциальным уравнением в частных про­изводных

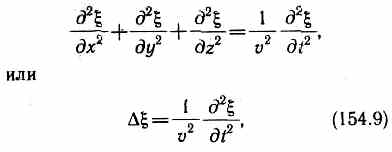
где v — фазовая скорость, D=д²/дx² +д²/дy²+д²/дz²— оператор Лапласа.Решением уравнения (154.9) является урав­нение любой волны. Соответствующей под­становкой можно убедиться, что уравне­нию (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сфериче­ская волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

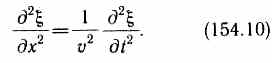
Эффект Доплера в акустике

Эффектом Доплера называется измене­ние частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т. е. движение источника колебаний (гудка) относительно приемни­ка (уха) изменяет частоту принимаемых колебаний.

Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямой; v_ист и v_пр — соответственно ско­рости движения источника и приемника, причем они положительны, если источ­ник (приемник) приближается к приемни­ку (источнику), и отрицательны, если уда­ляется. Частота колебаний источника рав­на v₀.

1. Источник и приемник покоятся от­носительно среды,т.е.v_ист=v_пр=0. Если v — скорость распространения звуковой волны в рассматриваемой среде, то длина волны l=vT=v/v₀. Распространяясь в среде, волна достигнет приемника и вы­зовет колебания его звукочувствительного элемента с частотой

n=v/l=v/(vT)=n₀

Следовательно, частота v звука, которую зарегистрирует приемник, равна частоте n₀, с которой звуковая волна излучается источником.

2. Приемник приближается к источни­ку, а источник покоится,т.е. v_пр>0, v_ист=0. В данном случае скорость распро­странения волны относительно приемника станет равной v+v_пр. Так как длина во­лны при этом не меняется, то

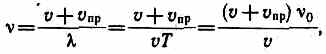
т. е. частота колебании, воспринимаемых приемником, в (v+v_пр)/v раз больше частоты колебаний источника.

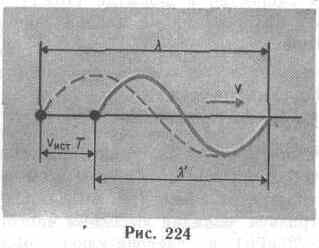3. Источник приближается к приемни­ку, а приемник покоится,т.е. v_ист>0, v_пр=0. Скорость распространения колеба­ний зависит лишь от свойств среды, поэто­му за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние vT (равное длине волны Я) независимо от того, движется ли источник или покоится. За это же время источник пройдет в на­правлении волны расстояние v_истT (рис.224), т.е. длина волны в направле­нии движения сократится и станет равной l'=l-v_истТ=(v-v_ист)Т, тогда

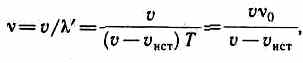
т. е. частота v колебаний, воспринимаемых приемником, увеличится в v/(v-v_ист)раз. В случаях 2 и 3, если v_ист<0 и v_пр<0, знак будет обратным.

4. Источник и приемник движутся от­носительно друг друга.Используя резуль­таты, полученные для случаев 2 и 3, можно записать выражение для частоты колеба­ний, воспринимаемых источником:

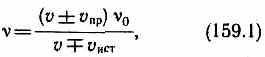
причем верхний знак берется, если при движении источника или приемника про­исходит их сближение, нижний знак — в случае их взаимного удаления.

Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или при­емник. Если направления скоростей v_пр и v_ист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.

Стоячие волны

Особым случаем интерференции являются стоячие волны— это волны, образующие­ся при наложении двух бегущих волн, рас­пространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. Для вывода уравнения стоячей волны предположим, что две плоские волны рас­пространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в кото­рой обе волны имеют одинаковую фазу, а отсчет времени начнем с момента, когда фазы обеих волн равны нулю. Тогда соответственно уравнения волны, распро­страняющейся вдоль положительного на­правления оси х, и волны, распространяю­щейся ей навстречу, будут иметь вид

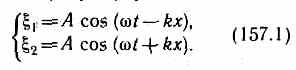
Сложив эти уравнения и учитывая, что k= 2p/l (см. (154.3)), получим уравнение стоячей волны:

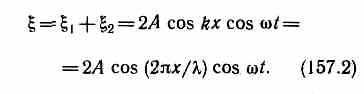
Из уравнения стоячей волны (157.2) вытекает, что в каждой точке этой волны происходят колебания той же частоты w с амплитудой А_ст=|2Аcos(2pх/l)|, зави­сящей от координаты х рассматриваемой точки.

В точках среды, где

2px/l=±mp (m=0, 1, 2, ...), (157.3)

амплитуда колебаний достигает макси­мального значения, равного 2 А. В точках среды, где

2px/l=±(m+1/2)p (m=0,1,2,...),

(157.4)

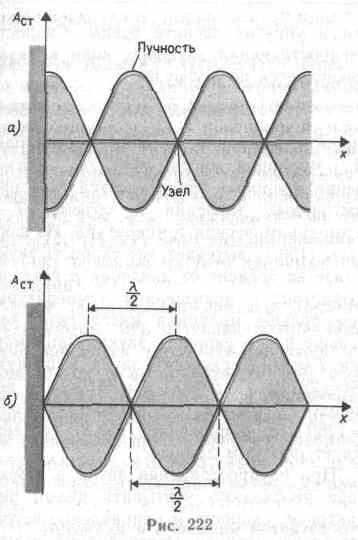
амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (A_ст=2А), называются пучностями стоячей волны,а точки, в ко­торых амплитуда колебаний равна нулю (A_ст=0), называются узлами стоячей во­лны.Точки среды, находящиеся в узлах, колебаний не совершают.

Из выражений (157.3) и (157.4) полу­чим соответственно координаты пучностей и узлов:

х₀=±тl/2 (m=0, 1,2, ...), (157.5)

х_узл=±(т+1/2)l/2 (m=0, 1, 2, ...).

(157.6)

Из формул (157.5) и (157.6) следует, что расстояния между двумя соседними пуч­ностями и двумя соседними узлами одина­ковы и равны l/2. Расстояние между соседними пучностью и узлом стоячей волны равно l/4.

В отличие от бегущей волны, все точки которой совершают колебания с одинако­вой амплитудой, но с запаздыванием по фазе (в уравнении (157.1) бегущей волны фаза колебаний зависит от координаты х рассматриваемой точки), все точки стоя­чей волны между двумя узлами колеблют­ся с разными амплитудами, но с одинако­выми фазами (в уравнении (157.2) стоя­чей волны аргумент косинуса не зависит от х). При переходе через узел множитель 2Аcos(2px/l) меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на p, т. е. точки, лежащие по разные стороны от узла, колеблются в противофазе.

Образование стоячих волн наблюдают при интерференции бегущей и отраженной волн. Например, если конец веревки за­крепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и об­разует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на гра­нице отражения узел или пучность, за­висит от соотношения плотностей сред. Если среда, от которой происходит отра­жение, менее плотная, то в месте отраже­ния получается пучность (рис. 222, а), ес­ли более плотная — узел (рис. 222, б). Об­разование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противо­положных направлений, в результате чего получается узел. Если же волна отражает­ся от менее плотной среды, то изменения фазы не происходит и у границы колеба­ния складываются с одинаковыми фаза­ми — получается пучность.

Если рассматривать бегущую волну, то в направлении ее распространения пе­реносится энергия колебательного движе­ния. В случае же стоячей волны переноса энергии нет, так как падающая и отражен­ная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. „Поэтому полная энергия результирующей стоячей волны, заклю

ченной между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных половине длины волны, происхо­дят взаимные превращения кинетической энергии в потенциальную и обратно.

28. 29. Средняя скорость и поток молекулосновное уравнение молекулярно-кинетической теории идеальных газов

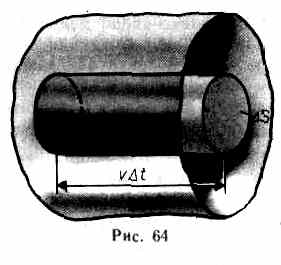
Для вывода основного уравнения молеку­лярно-кинетической теории рассмотрим одноатомный идеальный газ. Предполо­жим, что молекулы газа движутся хаоти­чески, число взаимных столкновений меж­ду молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS (рис. 64) и вычислим давле­ние, оказываемое на эту площадку. При каждом соударении молекула, движущая­ся перпендикулярно площадке, передает ей импульс m₀v-(-m₀v)=2m₀v, где т₀— масса молекулы, v — ее скорость. За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt (рис.64). Число этих молекул равно nDSvDt (n—концентрация молекул).

Необходимо, однако, учитывать, что реально молекулы движутся к площадке

DS под разными углами и имеют различ­ные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движе­ние молекул заменяют движением вдоль трех взаимно перпендикулярных направ­лений, так что в любой момент времени вдоль каждого из них движется ¹/₃ моле­кул, причем половина молекул (¹/₆) дви­жется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку DS будет ¹/₆nDSvDt. При столкновении с пло­щадкой эти молекулы передадут ей им­пульс

DР = 2m₀v•¹/₆nDSvDt=¹/₃nm₀v²DSDt.

Тогда давление газа, оказываемое им на стенку сосуда,

p=DP/(DtDS)=¹/₃nm₀v². (43.1)

Если газ в объеме V содержит N молекул,

движущихся со скоростями v₁, v₂, ..., v_N, то

целесообразно рассматривать среднюю квадратичную скорость

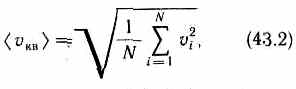
характеризующую всю совокупность моле­кул газа.

Уравнение (43.1) с учетом (43.2) при­мет вид

р = ¹/₃пт₀ <v_кв>². (43.3)

Выражение (43.3) называется основ­ным уравнением молекулярно-кинетической теории идеальных газов.Точный рас­чет с учетом движения молекул по все-

возможным направлениям дает ту же формулу.

Учитывая, что n = N/V, получим

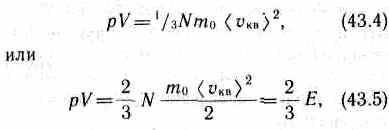
где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Так как масса газа m =Nm₀, то урав­нение (43.4) можно переписать в виде

pV=¹/₃m<v_кв>².

Для одного моля газа т = М (М — моляр­ная масса), поэтому

pV_m=¹/₃M<v_кв>²,

где V_m — молярный объем. С другой сто­роны, по уравнению Клапейрона — Мен­делеева, pV_m=RT. Таким образом,

RT=¹/₃М <v_кв>², откуда

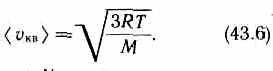
Так как М = m₀N_A, где m₀—масса од­ной молекулы, а N_А — постоянная Авогад­ро, то из уравнения (43.6) следует, что

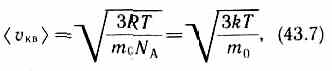
где k = R/N_A—постоянная Больцмана. Отсюда найдем, что при комнатной темпе­ратуре молекулы кислорода имеют сред­нюю квадратичную скорость 480 м/с, во­дорода — 1900 м/с. При температуре жид­кого гелия те же скорости будут соответ­ственно 40 и 160 м/с.

Средняя кинетическая энергия посту­пательного движения одной молекулы иде­ального газа

<e₀) =E/N = m₀ <v_кв>)²/2 = ³/₂kT(43.8)

(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической тем­пературе и зависит только от нее. Из этого уравнения следует, что при T=0 <e₀> =0,

т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии по­ступательного движения молекул идеаль­ного газа и формула (43.8) раскрывает молекулярно-кинетическое толкование температуры.