Число соударений и средняя длина свободного пробега молекул идеального газа
Молекулы газа в результате хаотического движения непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекула проходит некоторый путь λ, который называется длиной свободного пробега. В общем случае длина этого пути различна, но т.к. число столкновений очень велико, а движение беспорядочно, то при постоянных внешних условиях можно говорить о средней длине свободного пробега –  . Если молекулы данного газа испытывают за 1 секунду в среднем
. Если молекулы данного газа испытывают за 1 секунду в среднем 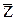 столкновений, то
столкновений, то
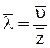 , (30)
, (30)
где 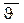 – средняя арифметическая скорость молекул.
– средняя арифметическая скорость молекул.
Молекулы идеального газа мы рассматриваем как шарики. Очевидно, что соударение произойдет, если две молекулы сблизятся до расстояния равного двум радиусам, т. е. диаметру молекул d. Минимальное расстояние, на которое сближаются при соударении центры двух молекул, называется эффективным диаметром молекул. Этот параметр зависит от 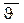 , а значит и от температуры газа.
, а значит и от температуры газа.
Для определения 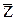 представим себе молекулу с эффективным диаметром d, которая движется со скоростью
представим себе молекулу с эффективным диаметром d, которая движется со скоростью 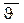 среди других молекул, которые при этом остаются неподвижными. Эта молекула столкнется со всеми молекулами, центры которых лежат внутри "ломаного" цилиндра радиусом d. Это значит, что
среди других молекул, которые при этом остаются неподвижными. Эта молекула столкнется со всеми молекулами, центры которых лежат внутри "ломаного" цилиндра радиусом d. Это значит, что 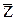 равно числу молекул в объеме этого цилиндра
равно числу молекул в объеме этого цилиндра
 , (31)
, (31)
 где n – концентрация молекул, а V–объём цилиндра:
где n – концентрация молекул, а V–объём цилиндра: 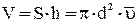 . С учётом этого –
. С учётом этого –
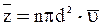 . (32)
. (32)
Учет движения других молекул увеличивает число столкновений в 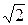 раз. Окончательно для z получим:
раз. Окончательно для z получим:
 . (33)
. (33)
Тогда 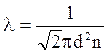 (34)
(34)
Т.к. p ~ n, то для разных внешних условий имеем:
 (35).
(35).
Для воздуха при н.у. (р = 760мм.рт.ст.; t0 = 00 С ): z = 109 c-1, а  = 5∙10-8 м.
= 5∙10-8 м.
