Лекция № 4. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

§ 1. Классификация событий. Опр.Событием в теории вероятностей называется всякий факт, который может произойти или не произойти в результате какого-то опыта (испытания). В теории вероятностей события обозначаются заглавными буквами латинского алфавита: А, В, С и т.д. или одной буквой, снабженной индексами: , , и т.д.

По возможности появления события делятся на достоверные, невозможные, случайные.

Опр.Достоверное событие - это такое событие, которое в результате данного испытания обязательно наступит.

Опр.Невозможное событие - это такое событие, которое в результате данного испытания не может произойти.

Опр.Случайное событие - это такое событие, которое в результате данного испытания может произойти, но может и не произойти.

Виды случайных событий.События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. События , ,… называются равновозможными, если условия их появления одинаковы.

Несколько событий образуют полную группу, если в результате испытания обязательно наступит хотя бы одно из них. На практике широкое применение находит полная группа несовместных событий. Два несовместных события, образующих полную группу, называются противоположными. Событие, противоположное событию А, принято обозначать .

§ 2. Элементы комбинаторики.Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном вычислении вероятностей. Комбинациями (соединениями) называют различные группы, составленные из каких-либо объектов. Элементами называются объекты, из которых составлены комбинации. Различают следующие три вида комбинаций: перестановки, размещения и сочетания.

Опр.Перестановками из элементов называют комбинации, содержащие все элементов и отличающиеся между собой лишь порядком элементов. Число перестановок из элементов находится по формуле .

Опр.Размещениями из элементов по в каждом называют такие комбинации, в каждую из которых входит элементов, взятых из данных элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения. Число размещений из элементов по находят по формуле .

Опр.Сочетаниями из эл-ов по называют комбинации, в каждую из которых входит элементов, взятых из данных эл-ов, и которые отличаются друг от друга по крайней мере одним эл-ом. Число сочетаний из элементов по находят по формуле . Для упрощения вычислений при полезно использовать следующее свойство сочетаний: .

§ 3. Классическое определение вероятности. Опр. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу, т.е. , где - число элементарных исходов, благоприятствующих наступлению события А; - число всех равновозможных элементарных исходов испытания.

Свойства вероятности: 1. Если А - достоверное событие, то 2. Если А - невозможное событие, то . 3. Если А - случайное событие, то . Следовательно, вероятность любого события удовлетворяет неравенствам .

§ 4. Теоремы сложения и умножения вероятностей. Опр. Суммой двух событий А и В называется событие С, состоящее в наступлении события А, или события В, или обоих событий вместе. Обозначается А+В=С. Если события и – несовместные, то событие + означает наступление одного из событий или .

Опр.Суммой нескольких событий , , … называется событие С, состоящее в наступлении хотя бы одного из этих событий. Обозначается С = + +…+ .

Опр.Произведением двух событий А и В называется событие С, состоящее в совместном наступлении события А и события В. Обозначается .

Опр.Произведением нескольких событийназывается событие, состоящее в совместном появлении всех этих событий. Обозначается С = … .

Т. слож. вер-ей несов. соб.Вер-ть суммы несовместных событий равна сумме вероятностей этих событий. .

След. 1. Если события , , …, образуют полную группу несовместных событий, то сумма их вероятностей равна единице: . След. 2. Сумма вероятностей противоположных событий равна единице: .

Теорема сложения вероятностей совместных событий.Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления: .

Опр. Два события называются независимыми, если вероятность наступления одного из них (причем любого) не зависит от того, произошло или не произошло другое событие. В противном случае события называются зависимыми.

Опр. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация из остальных событий (содержащая либо все события, либо часть из них) есть события независимые.

Опр. Условной вероятностью или называется вероятность события А, вычисленной в предположении, что событие В уже наступило.

Т. умножения вероятностей независимых событий.Вероятность произведения (совместного наступления) двух независимых событий равна произведению вероятностей этих событий: .

След. Вероятность произведения (совместного наступления) нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: .

Т. Вероятность появления хотя бы одного из событий , , … , незав. в совокупности, равна разности между единицей и произведением вероятностей противоположных событий , , … , т.е. .

Т. умножения вероятностей зависимых событий. Вероятность произведения (совместного наступления) двух зависимых событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: или .

§ 5. Формула полной вероятности. Формула Байеса.Пусть событие А может наступить при условии появления одного из несовместных событий , , … , образующих полную группу. Будем эти события называть гипотезами. Вероятность события А в этом случае вычисляется по формуле , которая носит название формулы полной вероятности.

Формула Байеса (вероятности гипотез).Пусть событие А может наступить при условии появления одного из несовместных событий , , …, , образующих полную группу. Вероятности этих гипотез до опыта известны и соответственно равны , , … . Произведен опыт, в результате которого наступило событие А. Вероятность гипотезы , после того, как событие А наступило, определяется по формуле Байеса , .

§ 6. Повторение испытаний. Формула Бернулли.Если в каждом из независимых испытаний вероятность появления события А постоянна и равна , то вероятность того, что в независимых испытаниях событие А наступит ровно раз, определяется по формуле Бернулли , где . На практике формулой Бернулли удобно пользоваться, если .

Формула Пуассона.Если производится достаточно большое число испытаний ( велико), в каждом из которых вероятность наступления события А постоянна, но мала, то вероятность того, что в испытаниях событие А наступит раз, определяется приближенно формулой , где .

Локальная т. Лапласа.Если производится независимых ис-ий ( - велико), и вероятность наступления события А в каждом испытании постоянна и равна , то вероятность того, что в независимых ис-ях событие А наступит раз, определяется по формуле , где , , причем результат тем точнее, чем ближе значение к и чем больше . Функция – четная, . Зам. Значения функции при , при полагают

Интегральная т. Лапласа.Если вер. наступления соб-я А в каждом из 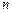независ. ис-ий постоянна и отлична от нуля и ед-цы, то вер. того, что в 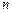независимых ис-ях событие А наступит не менее чем раз и не более чем раза, определяется по ф-ле , , , . Ф-я - нечетная, . При

Опр. Наивероятнейшим числом появления события А в независимых испытаниях называется число, для которого вероятность превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытаний. Наивероятнейшее число определяется по формуле ,где 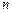- число независимых испытаний, - вероятность наступления события А в одном испытании, - вероятность не наступления события А в одном испытании, - наивероятнейшее число наступлений событий А.

§ 7. Случайные величины. Опр.Случайной называется величина, которая в результате опыта может принять одно и только одно возможное значение, неизвестно заранее, какое именно.

Опр.Случайная величина называется дискретной, если она принимает отдельные, изолированные друг от друга возможные значения, которые можно перенумеровать.

Опр.Непрерывной случайной величиной называется такая случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток, конечный или бесконечный. Случайные величины обозначаются: , , и т.д.

Опр.Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Для дискретной случайной величины закон распределения можно задать в виде таблицы ( – возм. значения случайной величины , – соответствующие им вероятности)

xi	x1	x2	x3	…	xn
pi	p1	р2	р3	…	рn

Опр. Интегральной функцией распределения случайной величины называется функция , выражающая вероятность того, что случайная величина примет значение меньшее, чем :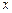

Св-ва интегральной функции 1. Значения интегральной функции принадлежат отрезку : . 2. - неубывающая функция, т.е. , если 3. 4. Вероятность того, что случайная величина примет значение в интервале , равна приращению интегральной функции на этом интервале: 5. Вероятность того, что непрерывная случайная величина примет одно конкретное значение, равна нулю, т.е. Поэтому для непрерывной случайной величины справедлива формула

Опр.Дифференциальной функцией распределения или плотностью распределения вероятностей случайной величины в точке называется отношение вероятности попадания непрерывной случайной величины на элементарный участок от 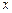до к длине этого участка, когда

Обозначается плотность вероятности через . По определению имеем: . Т.к. , то .

Т.о., если существует , то существует и , что обычно и предполагают. Интегральная функция выражается через дифференциальную формулой: .

Свойства дифференциальной функции распределения: 1. , т.е. дифференциальная функция неотрицательна. 2. . Вероятность того, что случайная величина примет значение, принадлежащее интервалу , равна единице.

3. Вер-ть того, что непр. случ. вел-на примет значение в интервале , равна опред. интегралу от дифференциальной функции распред., взятому в пределах от до : . Геом-ки эта вероятность равна площади кривол. трапеции.

§ 8. Числовые характеристики случайных величин. Опр.Математическим ожиданием случайной величины называется ее среднее значение, вычисляемое по формулам – для дискретной случ. величины, – для непрерывной случайной величины. Для встречающихся на практике случ. величин указанный несобственный интеграл сходится.

Свойства математического ожидания. 1. , где С – постоянная величина. 2. . 3. , если и – независимые случайные величины. 4. .

Опр.Разность между значением случайной величины и ее математическим ожиданием называется отклонением случайной величины , т.е. . Математическое ожидание отклонения равно нулю: .

Опр.Дисперсией случайной величины называется математическое ожидание квадрата отклонения: .

Дисперсия вычисляется по формулам: – для дискретной случайной величины, – для непрерывной случайной величины. Св-ва дисперсии: 1. , где С – пост. величина.

2. . 3. , если и - независимые случайные величины. 4.

Опр.Средним квадратическим отклонением случайной величины называется корень квадратный из дисперсии: