Представление произвольного сигнала в виде суммы элементарных колебаний
Для теории сигналов и их обработки важное значение разложение заданной функции 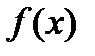 по различным ортогональным системам функций
по различным ортогональным системам функций 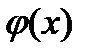 .
.
Бесконечная система действительных функций:
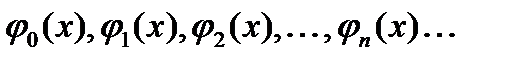
(1.3)
называется ортогональной на отрезке 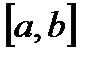 ,
,
если: 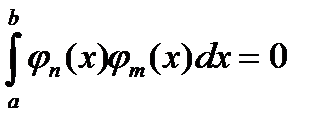 ,при
,при 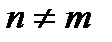
(1.4)
При этом предполагается, что: 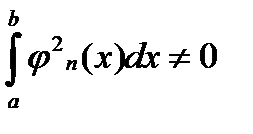
(1.5)
т.е. что никакая из функций рассматриваемой системы (1.3) не равна тождественно нулю.
Условие (1.4) выражает попарную ортогональность функций системы (1.3). Величина
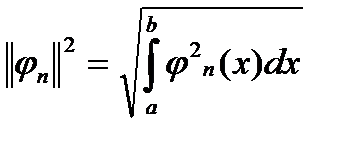
(1.6)
называется нормой функции 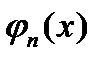 .
.
Функция 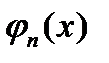 , для которой выполняется условие:
, для которой выполняется условие:
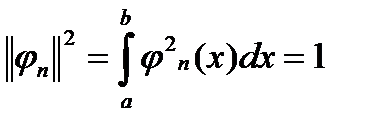 ,
,
(1.7)
называется нормированной функцией, а система нормированных функций 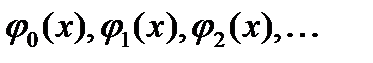 , в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.
, в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.
Если функции 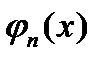 непрерывны, тогда произвольная кусочно-непрерывная функция
непрерывны, тогда произвольная кусочно-непрерывная функция 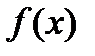 , для которой выполняется условие:
, для которой выполняется условие:
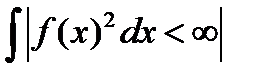 , может быть представлена в виде суммы ряда:
, может быть представлена в виде суммы ряда:
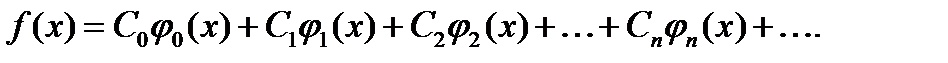
(1.8)
Умножим обе части выражения (1.8) на 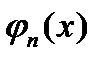 и проинтегрируем в пределах
и проинтегрируем в пределах 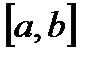 :
:
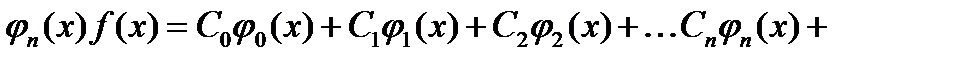
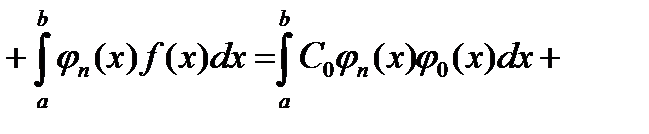
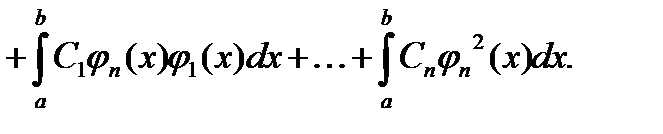
Все слагаемые вида 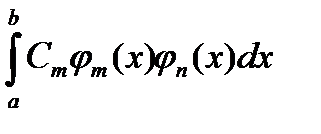 при
при 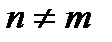 обращаются в нуль в силу ортогональности функций
обращаются в нуль в силу ортогональности функций 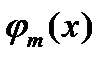 и
и 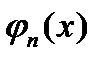 . В правой части остается одно слагаемое:
. В правой части остается одно слагаемое:
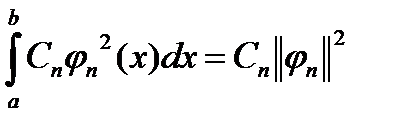 , что позволяет написать
, что позволяет написать
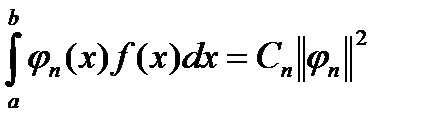
Откуда следует важное выражение:
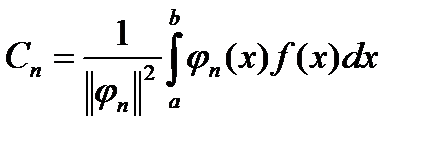
(1.9)
Ряд (1.8), в котором координаты 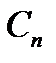 определяются по формуле (1.9), называется обобщенным рядом Фурье. По данной системе
определяются по формуле (1.9), называется обобщенным рядом Фурье. По данной системе 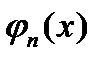 . Совокупность коэффициентов
. Совокупность коэффициентов 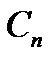 называется спектром сигнала.
называется спектром сигнала. 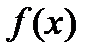 в ортогональной системе
в ортогональной системе 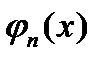 и полностью определяет етот сигнал.
и полностью определяет етот сигнал.
Для системы функций 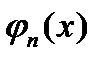 принимающих комплексные значения, приведенные выше определения обобщаются следующим образом:
принимающих комплексные значения, приведенные выше определения обобщаются следующим образом:
- условие ортогональности: 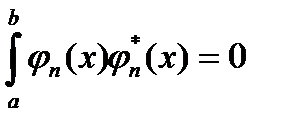 , при
, при 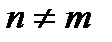 ;
;
- квадрат нормы функции: 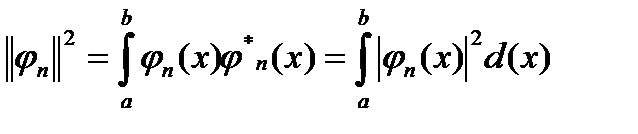 ;
;
- коэффициенты Фурье: 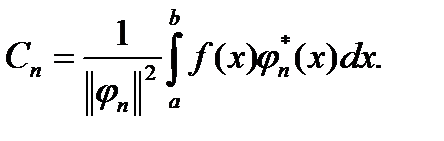 .
.
В этих выражениях 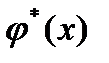 обозначает функцию, комплексно-сопряженную функции
обозначает функцию, комплексно-сопряженную функции 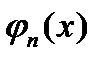 .
.
Применительно к сигналам 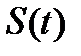 , являющимся функциями времени выражение (1.8) будет записываться в форме:
, являющимся функциями времени выражение (1.8) будет записываться в форме:
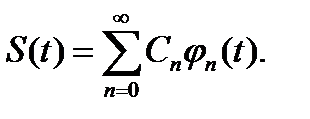
Квадрат нормы функции 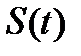 :
:
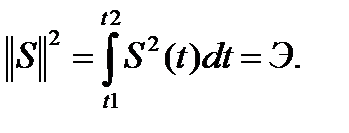
Таким образом, энергия сигнала:
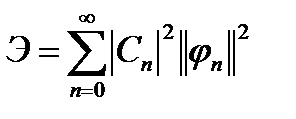
а при использовании ортонормированной системы функции 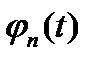 :
:
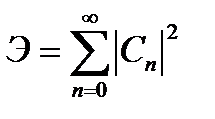
Очевидно, что средняя за время 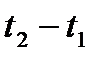 мощность сигнала:
мощность сигнала: 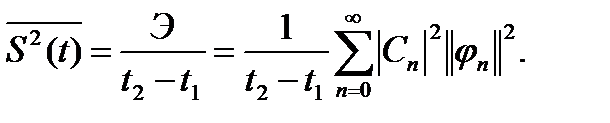
Наибольшее распространение получила ортогональная система основных тригонометрических функций-синусов и косинусов, Во-первых, гармонические функций (гармонические колебания) являются единственной функцией времени сохраняющей свою форму при прохождении через любую линейную цеп. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи.
