Импульс, энергия и масса в релятивистской механике

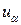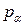Свойства инвариантной массы, связывающей и соотношением:

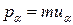, (1)

или, для 3-х мерного импульса

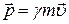, (2)

существенно отличаются от свойств, приписываемых массе в классической механике. Именно, масса покоя не удовлетворяет закону сохранения. Существуют процессы, при которых инвариантная масса частиц до начала процесса не равна массе частиц, сохранившихся после окончания процесса. Наличие массы покоя вообще не является обязательным свойством частиц. Существуют частицы с нулевой массой покоя - фотоны, нейтрино, например. Известно много процессов взаимного превращения частиц, при которых частицы с ненулевой массой покоя переходят в частицы с массой покоя, равной нулю. Конечно, при этом масса покоя не сохраняется.

Тем не менее, масса покоя – очень важная, фундаментальная характеристика частицы. Каждая элементарная частица имеет определённое, не изменяющееся от экземпляра к экземпляру значение массы покоя (включая и нулевое).

Так же, как о массе покоя элементарной частицы, можно говорить и о массе покоя тела, состоящего из множества элементарных частиц. При этом, однако, масса покоя системы частиц не равна сумме масс покоя отдельных частиц.

Из определения энергии частицы и четвертой компоненты импульса видно, что

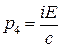. (3)

Это соотношение позволяет связать импульс и энергию в один 4-вектор энергии-импульса

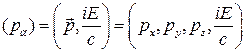. (6)

Компоненты 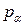преобразуются при переходе из одной ИСО к другой обычным образом, так что при движении, например вдоль оси x, для 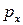и E имеем

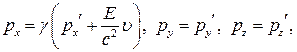(5)

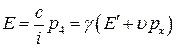. (5а)

Видно, что при преобразованиях Лоренца энергия и компоненты импульса выражаются друг через друга. Квадрат импульса – величина инвариантная:

,

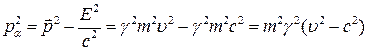т.е.

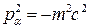. (6)

Следовательно, 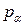- времениподобный вектор.

Рассмотрим случай 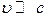.Тогда

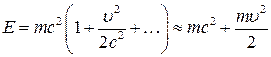. (7)

Второе слагаемое совпадает с кинетической энергией в классической механике. Но, оказывается, даже при 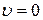энергия частицы вне поля сил

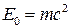(8)

отлична от нуля.

Такое определение энергии может показаться произвольным, поскольку Е можно было бы определить как

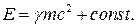(9)

Тогда, выбрав 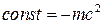, получим для энергии выражение, которое при 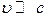совпадает с энергией частицы в классической механике.

Однако нельзя заранее требовать, чтобы все без исключения величины релятивистской механики при 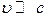приобретали классический вид. А вот преобразования Лоренца при 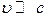обязаны совпадать с преобразованиями Галилея. Для этого должно выполняться условие 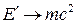, тогда

, ,

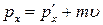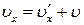следовательно, действительно нужно положить 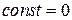в (9).

Таким образом, СТО приходит к новому важному выводу: покоящаяся частица обладает энергией 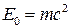. Её естественно назвать энергией покоя. Любая частица, имеющая массу покоя 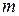, обладает в то же время энергией покоя 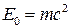. Энергия движущейся частицы равна

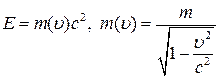. (10)

Формулы (8),(10) часто называют формулами Эйнштейна. Они показывают, что всякая частица, обладающая массой 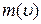( 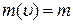, если 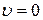) одновременно имеет энергию Е. При этом Е и 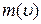пропорциональны друг другу.

Если на частицу не действуют внешние силы, то имеет место закон сохранения энергии

,

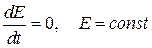и импульса

.

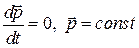Обычно Е называют полной энергией, хотя в неё не включена энергия частицы во внешнем поле. Иногда вводят кинетическую энергию 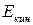, определяя её как энергию движения частицы

Так как 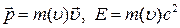, то

.
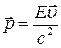