Центры тяжести простейших фигур

1. Центр тяжести треугольника.Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: A_i (x_i,y_i) , (i = 1,2,3) .

Разбивая треугольник на узкие полоски, параллельные стороне А₁А₂ , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А₃ М₃ (Рис.8.3)_.

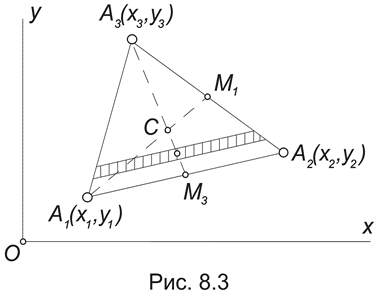
Разбивая треугольник на полоски, параллельные стороне А₂А₃, можно убедиться, что он должен лежать на медиане А₁М₁. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

В частности, для медианы А₁М₁ получим, учитывая, что координаты точки М₁ - это среднее арифметическое координат вершин А₂ и А₃ :

x_c = x₁ + (2/3)×(x_М1 - x₁) = x₁ + (2/3)× [(x₂ + x₃) /2 - x₁] = (x₁+ x₂ +x₃)/3.

Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:

x_c = (1/3)Sx_i ; y_c = (1/3)Sy_i .

2. Центр тяжести кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2a, расположенный симметрично относительно оси Ox (Рис.8.4) .

Очевидно, что y_c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле (8.2¢):

x_c = 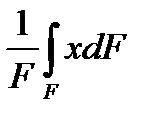. (8.5)

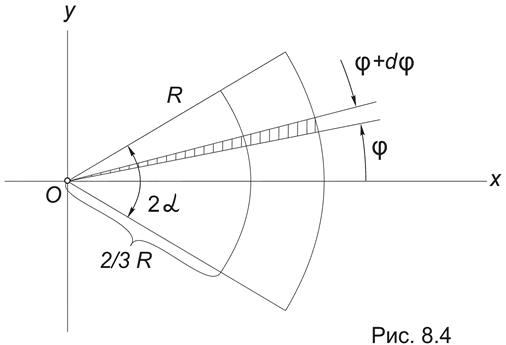
Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом dj. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R×dj и высотой R. Площадь такого треугольника dF = (1/2) R ²× dj, а его центр тяжести находится на расстоянии 2/3 R от вершины, поэтому в (8.5) положим x = (2/3)R×cosj. Подставляя в (8.5) F = a R ², получим:

x_c = = = = =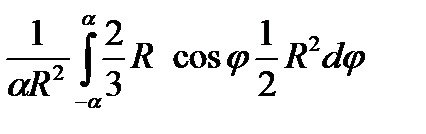

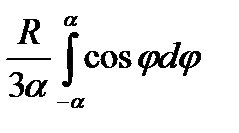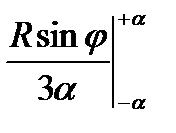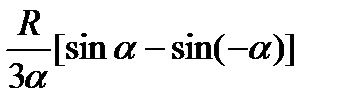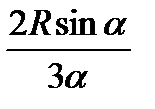= . (8.6)

С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.

Подставляя в (8.6) a = p/2, получим: x_c = (4R)/ (3p) @ 0,4 R .

Раздел II. Статика деформируемого тела

ГЛАВА 1. ВВЕДЕНИЕ

1.1. Предмет сопротивления материалов и его задачи

Раздел механики под названием «Статика деформируемого тела» большинство студентов изучает в курсе сопротивления материалов, поэтому мы сохраним за этим разделом такое название.

Как уже отмечалось, сопротивление материалов (СМ) является составной частью прикладной, технической или строительной механики.

В отличие от теоретической механики (ТМ), изучающей абсолютно твердое тело, СМ применяет модель деформируемого тела, которая в большей степени соответствует реальным объектам.

Замена модели вызывает отказ и от прежнего метода исследования. Если в ТМ, построенной на системе аксиом, применяется математический или аксиоматико-дедуктивный метод, то методом СМ является характерный для физики гипотетико-дедуктивный.

Напомним, что прикладная механика, в целом, служит решению задач проектирования, строительства и эксплуатации сооружений.

Основной задачей СМ является проектирование конструкций или их элементов, находящихся в определенных условиях, с учетом требований: прочности, жесткости, устойчивости, надежности, экономичности и эстетики.

Первые три требования являются необходимыми, поэтому при нарушении любого из них поиск проектного решения теряет смысл.

Прочность – способность конструкции не разрушаться под действием приложенной нагрузки или в результате какого-либо иного воздействия.

Жесткость – способность сохранять форму и размеры в заданных допустимых пределах.

Устойчивость –способность сохранять первоначальную форму равновесия при нагружении.

Отметим, что основная задача статики сооружений (СС) отличается от задачи СМ только масштабом – вместо конструкции или её элементов выступает сооружение.

Помимо основной задачи – проектирования – в СМ встречается задача расчета уже построенной конструкции: на допускаемую нагрузку, прочность, жесткость и т.д.

1.2. Расчетная схема и классификация систем

Для решения задачи СМ или СС нужно построить модель конструкции или сооружения, выделив основные несущие элементы и определив действующие на них нагрузки.

Такая модель в виде совокупности деформируемых тел, соединенных друг с другом определенными связями, называется расчетной схемой или системой.

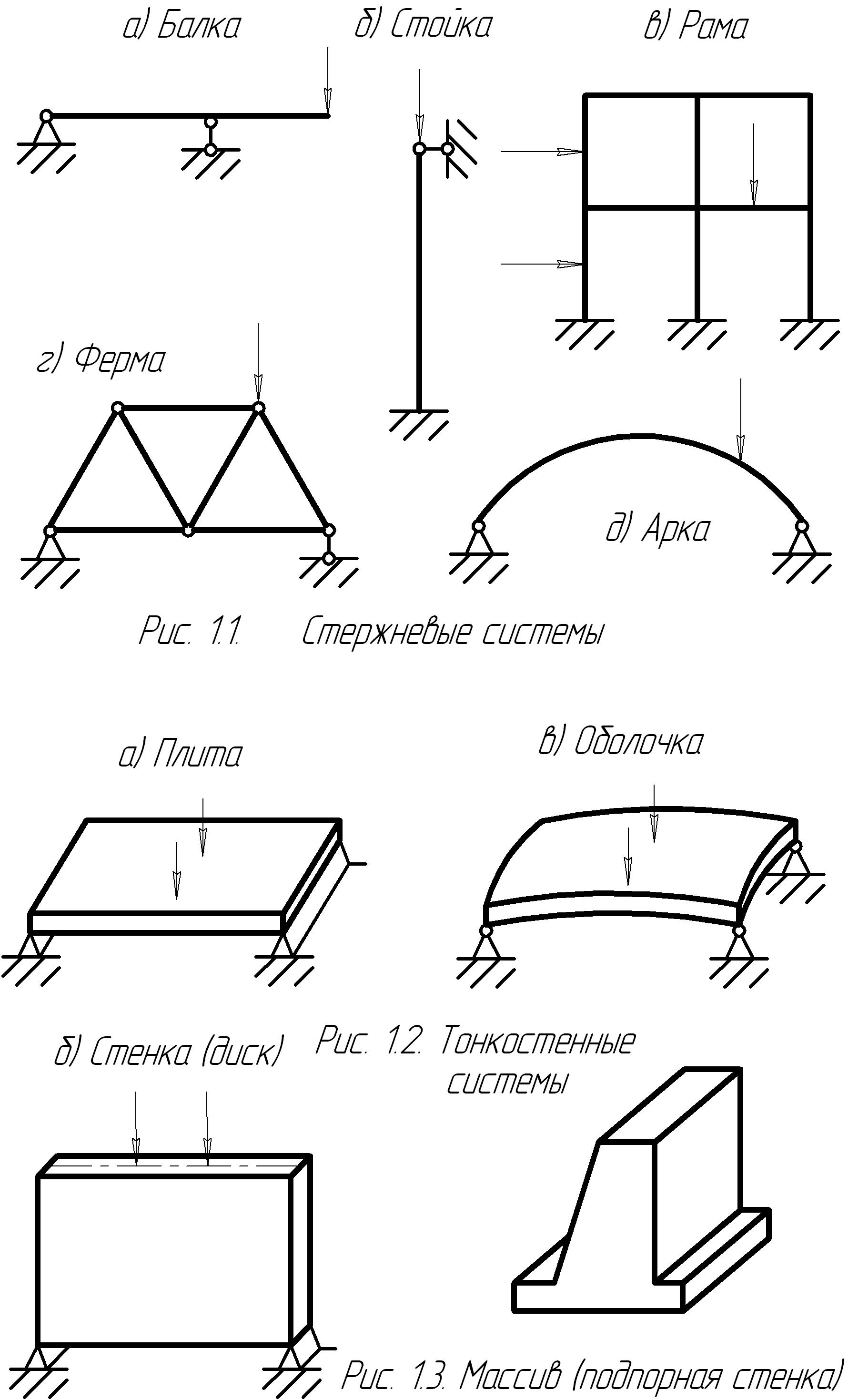
В зависимости от геометрических особенностей элементов системы их делят на три класса: стержневые, тонкостенные и массивы.

Стержень (брус) – тело, у которого один размер (длина) значительно больше двух других. Примеры конструкций, расчетная схема которых представляет собой брус или содержит такие элементы, приведены на рис 1.1.

Тонкостенные конструкции – это тела, у которых один размер (толщина) значительно меньше двух других (рис. 1.2.).

Массивами называются тела, у которых все три размера одного порядка. К ним относятся подпорные стенки (рис. 1.3.), фундаменты под отдельно стоящие колонны и т.п.

В общем случае расчетная схема сооружения может включать все три вида элементов.

ПРИМЕЧАНИЕ. Для кривых стержней, арок и оболочек речь при классификации систем идет не о габаритных, а о характерных размерах.

1.3. Нагрузки и воздействия

Все воздействия на конструкции и сооружения делятся на три группы: силовые, температурные и кинематические.

Два последних вида воздействий не оказывает влияния на опорные реакции и внутренние усилия статически определяемых систем, но могут вызвать появление реакций и усилий в статически неопределимых системах.

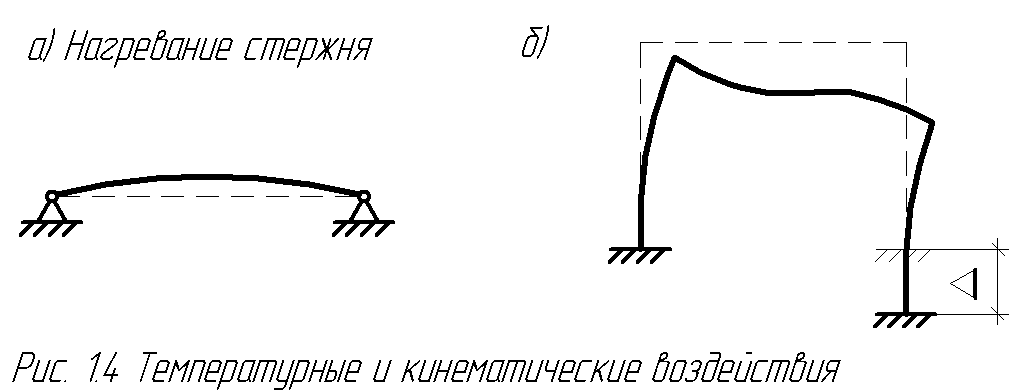
Например, при нагревании закрепленного на концах стержня может произойти либо потеря его устойчивости (рис. 1.4а), либо разрушение, а смещение фундамента опоры из-за просадки грунтового основания (рис. 1.4б) вызывает деформацию рамы и появление опорных реакций.

Что касается силовых воздействий или нагрузок, то мы уже встречались с ними в первом разделе курса ТМ и сейчас перейдем к уточнению этих понятий и их классификации.

Классификацию нагрузок можно проводить по различным признакам.

По характеру приложения они делятся на сосредоточенные (силы P или моменты M) и распределенные – по объему, по поверхности или вдоль длины балки – и определяемые интенсивностью.

Примером нагрузки, распределенной по объему тела, служит сила тяжести. Её интенсивность измеряется в кН/м³.

Интенсивность p поверхностной нагрузки (снег, ветер или давление грунта) имеет размерность давления и измеряется в кН/м² или килопаскалях (1кПа = 1кН/м²).

Интенсивность q нагрузки, распределенной по длине балки – с ней мы уже встречались в ТМ – измеряется в кН/м.

Помимо рассмотренных единиц измерения p применяют и более крупные: МПа = кПа×10³ = Па×10⁶ и ГПа = кПа 10⁶.

По динамическим характеристикам нагрузки подразделяются на статические, динамические и повторно-переменные (циклические).

Статическими называются неподвижные или медленно изменяющиеся подвижные нагрузки.

Динамическими являются нагрузки, у которых величина, точка приложения или направление меняются столь быстро, что при расчете необходимо учитывать силы инерции. К их числу относятся: импульсные, вибрационные, сейсмические и другие нагрузки.

Циклическими называются нагрузки, которые многократно (сотни тысяч раз) меняют свою величину и знак и могут вызывать усталостное разрушение материала конструкции.

По продолжительности воздействия различают постоянные и временные нагрузки.

Первые действуют в течение всего периода эксплуатации сооружения и представлены, например, собственным весом конструкций.

Временные нагрузки действуют на протяжении ограниченного промежутка времени. К ним относится нагрузка от веса людей и оборудования снеговая и др.

Подробнее о нагрузках можно узнать в СНиП 2.01.07–85 «Нагрузки и воздействия».

ПРИМЕЧАНИЯ:

1.Если в ТМ понятие «сосредоточенная сила» является строгим, то в механике деформируемого тела этот термин может применяться только условно – для нагрузки, распределенной по сравнительно небольшой площади. Например, – по области контакта двух деформируемых тел.

2. То же самое справедливо в отношении сосредоточенного момента М, приложенного к балке в сечении x=х_М. В ТМ он определяется как система, полученная из пары сил ±P=M/2e, приложенных в точках х=х_М±e, при e®0.

Вместе с тем применение термина «сосредоточенная нагрузка» допустимо в СМ в ходе построения расчетной схемы и на стадии предварительного расчета при определении внутренних усилий – в соответствии с принципом отвердевания из ТМ.

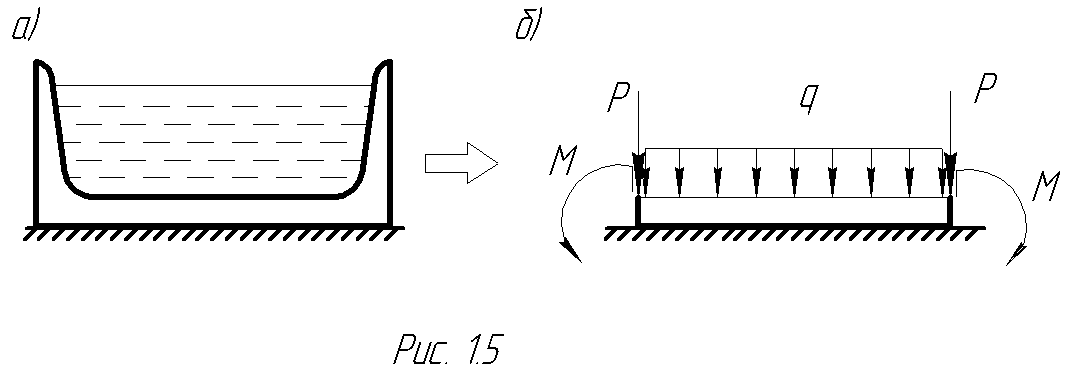
Например, расчетной схемой днища резервуара П-образного поперечного сечения (рис. 1.5а) служит балка на упругом основании, загруженная распределенной нагрузкой – от веса воды, а также сосредоточенными моментами и силами на концах – от давления воды на стенки резервуара и их собственного веса (рис. 1.5б).

3. Некоторые авторы наряду с распределенной силовой рассматривают распределенную моментную нагрузку. В соответствии с приведенными выше замечаниями, мы ограничимся учетом только первой из них.

1.4. Гипотезы сопротивления материалов

Для обоснования возможности применения аппарата математики и проведения теоретических исследований и расчетов в СМ вводят предпосылки, отражающие свойства деформируемых тел. Справедливость этих гипотез, в отличие от аксиом ТМ, проверяется экспериментально. Приведем только некоторые из них, т.к. другие удобнее рассматривать по мере необходимости.

1. Гипотеза однородности среды означает, что материал тела предполагается сплошным (без пустот), однородным и изотропным, т.е. свойства материала одинаковы во всех направлениях.

2. Гипотеза идеальной упругости – тело полностью восстанавливает свои размеры и форму после снятия приложенной нагрузки. При этом результат воздействия зависит от приложенной нагрузки, но не от истории загружения.

3. Гипотеза малости перемещений означает, что перемещения точек тела малы в сравнении с его размерами. Для консольной балки (рис. 1.6а) это означает, что D(R )<< l.

Следствием этой гипотезы является принцип начальных размеров, в соответствии с которым уравнения равновесия деформированного тела составляют без учета перемещений точек приложения нагрузки, т.е. как для абсолютно твердого. В рассмотренном примере это означает, что для деформированной балки по-прежнему M_A(P)=Pl, т.е. при вычислении момента силы P можно пре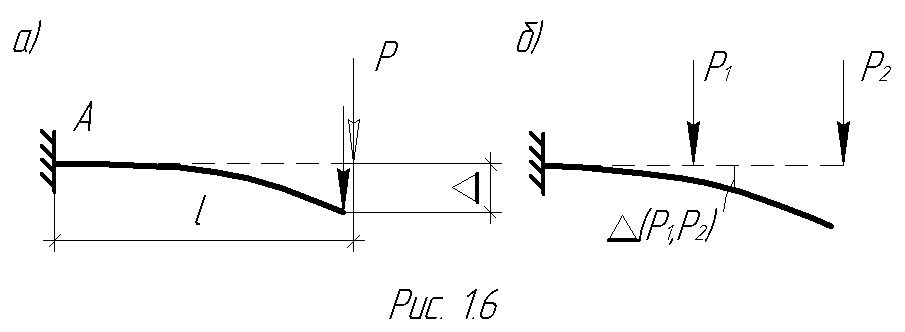
небречь горизонтальным перемещением точки ее приложения.

4. Гипотеза линейной упругости – перемещение точки упругого тела пропорционально приложенной нагрузке.

В рассматриваемом примере (рис. 1.6а) это означает, что n-кратное увеличение силы P вызывает n-кратное увеличение перемещения любой фиксированной точки этой балки: D (nP) = n×D (Р).

ПРИМЕЧАНИЯ:

1. Следствием гипотез 3 и 4 является принцип суперпозиции, который справедлив для любых линейных систем и представляет собой обобщение соответствующего принципа из ТМ: опорные реакции, усилия и перемещения от заданной нагрузки можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.

В рассматриваемом примере это означает (рис. 1.6б), что перемещение любой фиксированной точки балки от совместного воздействия сил P₁ и P₂ можно найти как сумму перемещений этой точки от каждой силы в отдельности:

D (P_1, P₂) = D (R₁) + D (R₂).

2. Если какая-либо из приведенных гипотез или построенная на ее основе теория не подтверждаются опытом для определенного класса материалов и конструкций, возникает необходимость в построении новой теории. Например, древесина и композиционные материалы обладают анизотропными свойствами, учет которых требует пересмотра формулировки первой гипотезы.

3. Применение в СМ методов ТМ возможно только в соответствии с рассмотренной выше гипотезой 3 и принципом отвердевания на предварительном этапе расчета при составлении уравнений равновесия.

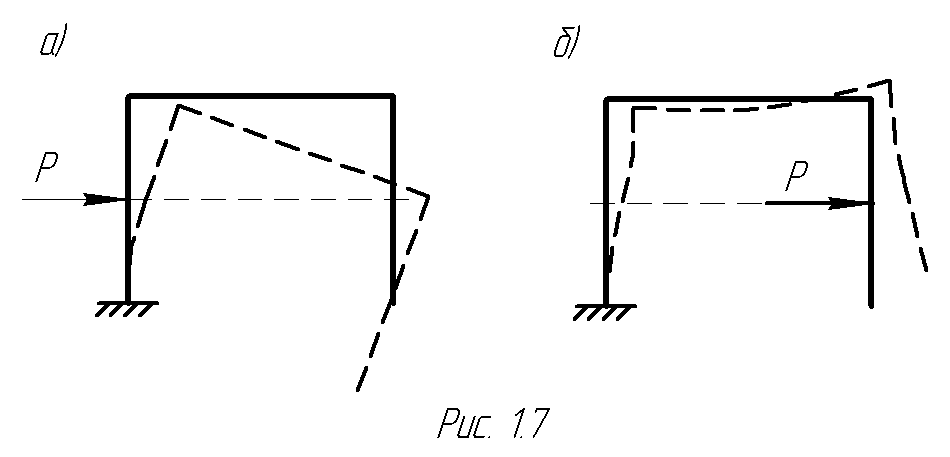
Использование в СМ аксиом ТМ на последующих этапах расчета недопустимо. Нельзя, например, переносить силу, приложенную к деформируемому телу, вдоль линии ее действия, поскольку при этом могут полностью измениться внутренние усилия и перемещения точек системы, несмотря на постоянство опорных реакций (рис. 1.7).

1.5. Метод сечений. Напряжения

Для расчета на прочность нужно знать, какие силы появляются в каждой внутренней точке тела в ответ на действие внешних сил. Для их определения воспользуемся обобщением принципа освобождаемости от связей из ТМ, сделав внутренние силы внешними.

Рассмотрим тело под действием уравновешенной системы сил (рис. 1.8а). Проведем через интересующую нас точку М плоскость и рассмотрим часть тела слева от сечения с нормалью n (рис. 1.8б). Помимо внешних сил Р₁ и Р₂на нее будет действовать реакция отброшенной правой части, не показанная на рисунке. Эту реакцию в виде распределенной по площади сечения поверхностной нагрузки и будем называть напряжением.

Выясним, чем отличается напряжение от обычного давления. Как известно из ТМ, реакция связи направлена в сторону, противоположную той, куда тело не может перемещаться из-за наложенной связи. Поэтому если бы напряжение, как и давление, было направлено по нормали n, части тела, расположенные по обе стороны от плоскости воображаемого сечения, могли бы беспрепятственно смещаться друг относительно друга вдоль этой плоскости. Наш опыт свидетельствует об обратном, поэтому можно сделать вывод, что в общем случае напряжение является вектором, который направлен под углом к нормали n в каждой точке сечения.

Разложим вектор напряжения p по правилу параллелограмма на нормальную и касательную составляющие:

p =s + t,

где s || n, а t^ n.

Эти напряжения можно наглядно показать на рисунке, если рассмотреть тело в плоскости, ортогональной к проведенному сечению. Поскольку при этом

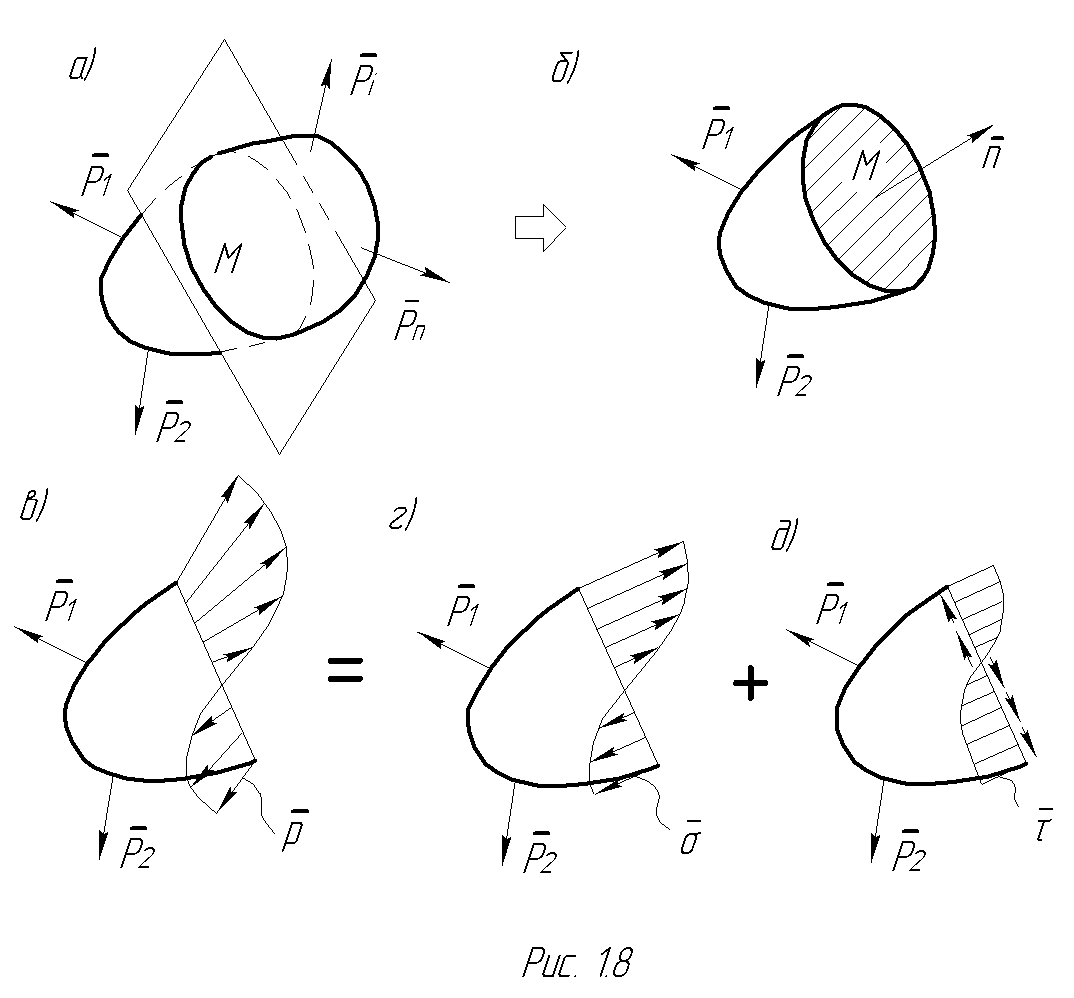
все векторы t будут расположены вдоль одной прямой, их величины в каждой точке сечения условно откладывают в направлении нормали n (рис. 1.8 в-д).

Последовательней и удобней заменить построение векторов sи t построением эпюр их проекций на эту нормаль и перпендикулярные к ней направления, как и принято в СМ.

Эти напряжения и нужно знать для расчета тела на прочность. Как их найти? Для тел простой формы - из условий равновесия отсеченной части, как обычно в ТМ находят реакции опор. При этом, в соответствии с принципом отвердевания, можно воспользоваться теоремой о приведении пространственной системы сил, согласно которой произвольная система сил эквивалентна главному вектору R₀ и главному моменту M₀:

(Р₁, Р₂, …, Р_n) ~ (R₀, М₀).

ПРИМЕЧАНИЯ:

1. В СМ нередко отождествляют понятия вектора напряжения и его проекции, говоря об «эпюре напряжений» или о «положительном направлении» этого вектора.

2. Если тремя парами параллельных плоскостей вырезать из тела куб, то напряжения, действующие по его граням и соответствующие положительным значениям их проекций, в общем случае можно обозначить так, как показано на рис. 1.9. В дальнейшем для касательных напряжений нам будет удобнее изменить эти направления на противоположные.

3. Мы предполагаем, что напряжения в сечении тела могут появляться только в ответ на действие внешних сил, и равны нулю при их отсутствии, что соответствует гипотезе ненапряженного начального состояния.