Теорема. Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность - по окружности, с центром на оси конуса

Самостоятельная работа №18

Тема: «Цилиндры, конусы, шар и сфера»

Выполнил:

Студент группы М-159

Гончаров В.В.

Бабенко Р.Г.

Проверил:

Преподаватель математики

Яндович Олег Алексеевич

Учебный год

Оценка за работу ________________

Цилиндр

Цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси.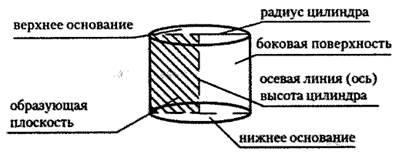

Круги называются основанием цилиндра, а отрезки - образующими цилиндра. Так же, как и для призмы доказывается, что основания цилиндра равны и лежат в параллельных плоскостях, образующие параллельны и равны.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Радиусом ц. называется радиус его основания. Высота - расстояние между плоскостями оснований. Ось - прямая, проходящая через центры основан. Сечение ц. плоскостью, проходящей через ось ц. - осевое сечение.

Теорема. Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Доказательство. Пусть б - плоскость, перпендикулярная оси цилиндра. Эта плоскость || основаниям. Параллельный перенос в направлении оси ц., совмещающий плоскость б с плоскостью основания ц., совмещает сечение б.п плоскостью б с окружностью основания. Ч.Т.Д.

Призмой, вписанной в цилиндр, называется такая п., основания которой - равные многоугольники, вписанные в основание ц. Призма называется описанной около ц., если ее основания - равные многоугольники, описанные около основания ц.

. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.

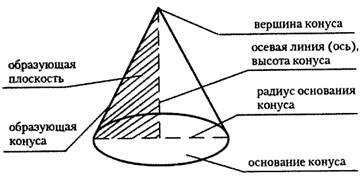
Отрезки, соединяющие вершину к. с точками окружности основания, называются образующими конуса. К. называется прямым, если прямая соединяющая вершину к. с центром основания, перпендикулярна плоскости основания.

Высотой к. называется перпендикуляр, опущенный из его вершины на плоскость основания.

Осью прямого конуса называется прямая, содержащая его высоту. Сечение к. плоскостью, проходящей через его ось, называется осевым сечением.

Плоскость, проходящая через образующую к. и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса.

Теорема. Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность - по окружности, с центром на оси конуса.

Док-во. Пусть б - плоскость, перпендикулярная оси конуса и пересекающая к. Преобразование гомотетии относительно вершины к., совмещающее плоскость б с плоскостью основания, совмещает сечение к. плоскостью б с основанием к. Следовательно, сечение к. плоскостью есть круг, а сечение б.п. - окружность с центром на оси конуса.

Плоскость, перпендикулярная оси конуса, отсекает он него меньший к. Оставшаяся часть называется усеченным к. Ч.Т.Д Пирамидой, вписанной в конус, называется такая пирамида, основанность основания конуса, а вершиной является вершина конуса. Пирамида называется описанной около конуса, если ее основанием является многоугольник, описанный около основания к., а вершина совпадает с вершиной к.

СФЕРА И ШАР