Проекции геометрических тел и точек, расположенных на их поверхности

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. А.Н. ТУПОЛЕВА-КАИ»

Институт авиации, наземного транспорта и энергетики

КафедраМашиноведения и инженерной графики

Е.В. Архипова, Л.Ш. Хаиров

Проекционное черчение

с элементами начертательной геометрии

Учебное пособие для студентов 1-го курса

Казань, 2015

Учебное пособие подготовлено для студентов очной формы обучения первого курса дневного отделения КГТУ им. А.Н. Туполева.

Содержание

	Проекции геометрических тел и точек, расположенных на их поверхностях	4 стр.
	Сечения поверхностей геометрических тел проецирующими плоскостями 2.1.Построение сечения многогранника 2.2.Построение сечения тел вращения	16 стр.     19 стр.   20 стр.
	Проекции геометрических тел со сквозными отверстиями	24 стр.
	Разрезы	27 стр.
	Аксонометрические проекции	29 стр.
	Вопросы для самоконтроля	38 стр.
	Примеры выполненных работ	40 стр.

Пpавила изобpажения пpедметов на чеpтежах устанавливает ГОСТ 2.305-68.

В соответствии с ГОСТом предметы должны изображаться по методу прямоугольного проецирования на плоскости.

В качестве основных плоскостей проекций пpинимают гpани пустотелого куба, в котоpый мысленно помещают пpедмет и пpоециpуют его на внутpенние повеpхности гpаней. Гpани совмещают с плоскостью, как показано на pис. 1.

Между пpедметом и его пpоекцией существует взаимно однозначное точечное соответствие, котоpое состоит в том, что каждой точке пpедмета соответствует опpеделенная точка на пpоекции и наобоpот.

Построение проекций предметов (геометрических тел) на чертежах является содержанием проекционного черчения.

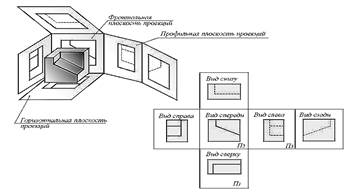
Рис. 1.

Проекции геометрических тел и точек, расположенных на их поверхности

Большинство технических деталей представляют собой сочетание простых геометрических тел, которые пересекаются между собой и переходят друг в друга, образуя сложную форму детали (рис. 2).

Рис.2

К базовым геометрическим телам относятся: конус, цилиндр, сфера, тор, призма и пирамида.

Конус -геометрический объект, ограниченный линейчатой конической поверхностью и плоскостью основания (рис. 3а). Конус может быть прямым или наклонным.

Цилиндр (рис. 3б) – это геометрический объект, ограниченный линейчатой цилиндрической поверхностью и двумя плоскостями основаниями. Различают прямые и наклонные цилиндры.

Сфера – это геометрический объект, поверхность которого образуется вращением окружности вокруг оси, лежащей в плоскости этой окружности и проходящей через её центр (рис.3в).

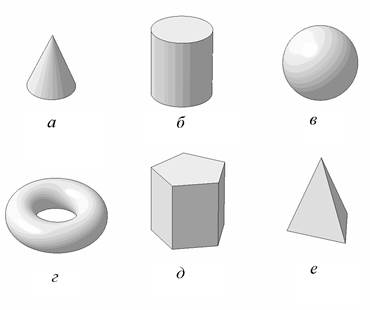
Рис. 3.

Тор– это геометрический объект, поверхность которого образуется вращением окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 3г).

Призма- многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторона­ми, а все другие грани - параллелограммы (рис. 3д). Если основанием приз­мы является параллелограмм, то такая призма называется па­раллелепипед. Призма называется прямой, если ее ребра перпендикулярны плоскости основания. Пря­моугольный параллелепипед, все ребра которого равны между собой, называется кубом.

Пирамида- это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной (рис. 3е). Пи­рамида называется правильной, если в основании лежит правильный многоугольник и высота пирами­ды проходит через центр многоугольника.

***

При выполнении чертежей часто возникает необходимость построения точек или линий, принадлежащих поверхности детали. Эта задача сводится к нахождению недостающих проекций точек принадлежащих заданной поверхности. Построение точек на поверхности является одной из главных задач в проекционном черчении, так как к ней сводятся задачи определения точек пересечения прямой и поверхности, определения линий пересечения плоскости и поверхности, двух поверхностей.

Решение этих задачи основано на известном положении: точка принадлежит поверхности в том случае, если она принадлежит линии этой поверхности. В качестве таких линий выбирают графически простые линии: прямые или окружности.

Так, например, на поверхности призмы (рис. 4) прямая MN параллельна ребру призмы, на которой намечена точка K, принадлежащая грани призмы, на поверхности прямого кругового конуса можно выбрать образующую ST или параллель a.

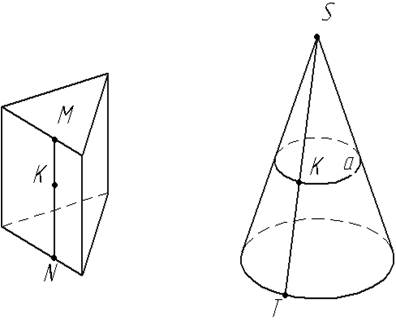
Рис. 4.

С целью упрощения изображения детали и облегчения чтения его чертежа предмет располагают относительно плоскостей проекций так, чтобы основные его элементы проецировались без искажений. Например, призму, пирамиду, цилиндр и конус располагают таким образом, чтобы их основания были параллельны плоскости проекций (Рис. 5).

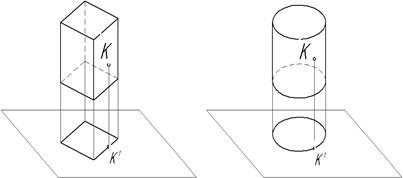
Рис. 5.

***

Прочитать чертёж детали означает представить её форму по имеющимся изображениям проекций. Чтение изображения начинают с чтения линий на чертеже. Любая линия, принадлежащая изображению фигуры, может быть изображением границы поверхности. Границей поверхности может быть и линия пересечения этой поверхности с другой.

Например, для правильной шестиугольной призмы, чертеж которой в двух проекциях дан на рис. 6, горизонтальная проекция представляет собой шестиугольник, каждая из сторон которого является проекцией боковой грани, а вершины – проекциями боковых ребер призмы.

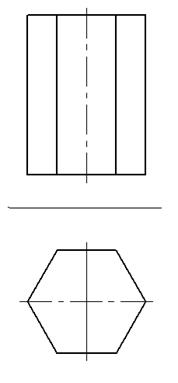
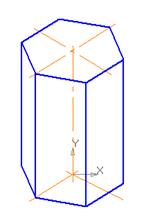
Рис. 6.

Выполнять чертеж следует без указания осей проекций. Например, для построения, профильной проекции передней грани призмы (рис. 7) измеряют отрезок, выражающий координату этой грани, на горизонтальной проекции, и откладывают его на профильной проекции.

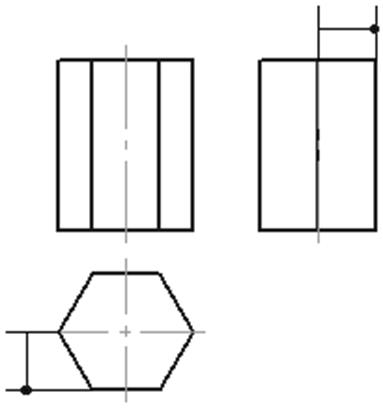
Рис. 7.

Для построения проекции точки, принадлежащей поверхности тела, надо сначала определить вид этой поверхности, установить её границы, найти проекции поверхности, а затем уже строить проекции заданной точки.

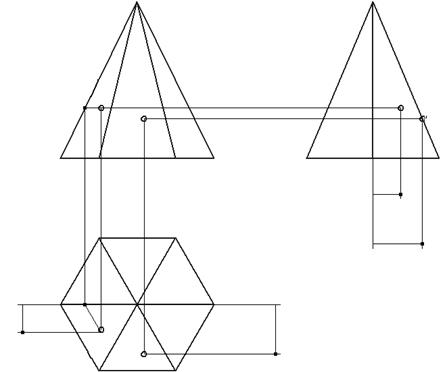
Рис. 8.

На рис.8 дан чертёж прямой шестиугольной пирамиды. Основание пирамиды расположено параллельно горизонтальной плоскости проекций. Контур горизонтальной проекции пирамиды образован сторонами правильного шестиугольника, представляющего собой горизонтальную проекцию основания пирамиды. Линии, соединяющие центр с вершинами – это проекции боковых рёбер пирамиды. Боковые грани пирамиды представляют собой треугольники. Их горизонтальные проекции также треугольники. Контуры фронтальной и профильной проекций образованы сторонами равнобедренных треугольников, основания которых – соответствующие проекции основания пирамиды. Точку на поверхности пирамиды находят по её принадлежности образующей или параллели.

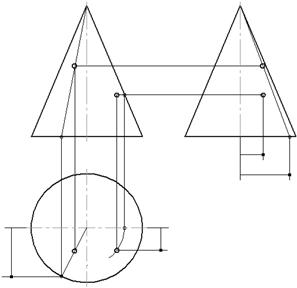
Рис. 9.

На рис.9 дан чертеж прямого кругового конуса, ось которого перпендикулярна горизонтальной плоскости. Горизонтальная проекция тела – круг, являющийся одновременно горизонтальной проекцией основания конуса и его боковой поверхности. Центр этого круга – горизонтальная проекция вершины конуса. Фронтальная и профильная проекции тела – равнобедренные треугольники, боковые стороны которых – проекции соответствующих образующих. Точку на поверхности конуса находят по её принадлежности образующей или параллели.

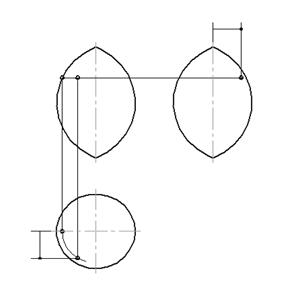
Рис. 10.

На рис.10 изображен тор, который образован вращением дуги вокруг оси – хорды.

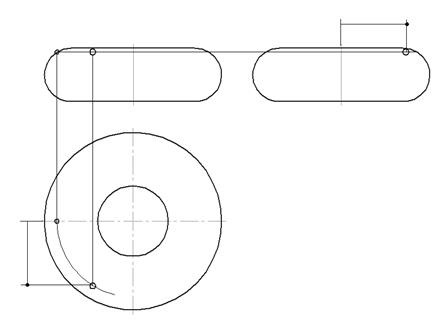
Рис. 11.

На рис.11 изображен тор, образованный вращением окружности вокруг оси, не пересекающейся с окружностью. Такой тор называется кольцом. Точки на поверхности тора находят по её принадлежности к параллели.