Производная и дифференциал

МАТЕМАТИКА

Методические указания и контрольные задания 1 и 2

для студентов-заочников 1-го курса

Составители: Е. В. Наумова Э.Н. Осипова Г.П. Мещерякова Л. И. Король

Санкт-Петербург

	РЕКОМЕНДОВАНО на заседании кафедры 25.12.2003 г., протокол № 4
	Рецензент Н. Ф. Мартынова

Оригинал подготовлен в ИПЦ СПГУТД

Изд. лиц. № 000 285 от 21.10.99

Подписано к печати 20.02.2004. Формат 60 84 1/16

Печать трафаретная

Усл. печ. л. 3,9. Заказ .Тираж 200 экз.

Отпечатано в типографии СПГУТД

191028, Санкт – Петербург, ул. Моховая, 26.

В методических указаниях приведены примеры и задачи по следующим разделам курса математики:

1. Элементы линейной алгебры.

2. Векторная алгебра.

3. Геометрия на плоскости.

4. Введение в математический анализ.

5. Производная и дифференциал.

6. Исследование поведения функции.

В течение семестра Вы должны выполнить и сдать на проверку две контрольных работы:

контрольная работа № 1 включает темы 01 – 03,

контрольная работа № 2 - темы 04 - 06.

В контрольной работе № 1 каждый студент должен решить и представить на рецензию 3 задания, а в контрольной работе № 2 – четыре задания, которые могут содержать по несколько примеров. Каждая контрольная должна быть выполнена в отдельной тетради.

Контрольная работа № 1 должна быть представлена на проверку в середине семестра, а контрольная работа № 2 – не позднее, чем за две недели до начала экзаменационной сессии.

Если все задания выполнены без ошибок, то студент допускается к защите этих работ, которая происходит во время экзаменационной сессии перед экзаменом по математике. Если в работе есть ошибки, то их нужно исправить в этой же тетради и прислать на повторную проверку.

Прежде чем приступать к выполнению контрольных работ, студенту необходимо изучить соответствующий теоретический материал по указанным учебникам. По каждой теме дается список вопросов, на которые необходимо ответить при подготовке к экзамену.

Если в процессе изучения теорем или при решении задач возникают вопросы, то можно обратиться к преподавателям кафедры математики для получения письменной или устной консультации.

Во время экзаменационной сессии для студентов-заочников организуются лекции и практические занятия, которые носят обзорный характер.

При выполнении контрольной работы обратите внимание на оформление работы. на титульном листе должны быть указаны:

фамилия, имя, отчество.

Номер студенческого билета (или зачетной книжки).

Название дисциплины и номер контрольной работы.

Номер варианта.

Номер варианта, который должен выполнять студент, соответствует последней цифре номера студенческого билета (или зачетной книжки).

В каждом задании 20 вариантов примеров. Если год Вашего поступления в Университет – чётный, то Вы выбираете пример из первых десяти вариантов, а если – нечётный, то выбираете свой вариант из номеров с десятого по двадцатый.

ЛИТЕРАТУРА

1. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.1., 2., 2003 г.

2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры, 2005 г.

3. Берман Г.Н. Сборник задач по курсу математического анализа, 2005 г.

4. Ильин В.А. и др. Аналитическая геометрия, 2009 г.

5. Кузнецов Л.А. Сборник задач по высшей математике, 2005 г.

6. Шнейдер В.Е. и др. Краткий курс высшей математики, т.1. , 1978 г.

7. Шнейдер В.Е. и др. Краткий курс высшей математики, т.2. 1978 г.

8. Кремер Н.Ш. и др. Математика для экономистов, 2010 г.

9. Ермаков В.И. и др. Общий курс высшей математики для экономистов, 2002 г.

10. Минорский В.П. , Сборник задач по высшей математике, 2006 г.

11. Данко П.Е., Попов А.Г. и др., Высшая математика в упражнениях и задачах, т.т. 1-2, 2002 г.

12. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов, 2002 г.

13. Ермаков В.И. и др. Сборник задач по высшей математике для экономистов, 2002г.

Вопросы для самопроверки

Линейная алгебра

1. Что называется матрицей? Как определяются линейные операции над матрицами?

2. Что называется определителем? Каковы основные свойства определителей? Что называется минором и алгебраическим дополнением?

3. Каковы способы вычисления определителей?

4. Напишите формулы Крамера. В каком случае они применимы?

5. Что называется рангом матрицы? Как его можно найти?

6. Что такое матрица системы и расширенная матрица системы линейных уравнений?

7. Какие системы называются совместными и какие несовместными? Сформулируйте теорему Кронекера – Капелли.

8. В чем заключается метод полного исключения для решения систем линейных уравнений?

Векторная алгебра

1. Что называется вектором и как он изображается?

2. Какие векторы называются равными, противоположными, коллинеарными, компланарными?

3. Какие операции над векторами называются линейными и каковы свойства этих операций?

4. В каком случае векторы называются линейно независимыми и в каком – линейно зависимыми?

5. Что называется базисом на прямой, плоскости и в пространстве?

6. Сформулируйте правила линейных операций над векторами, заданными своими координатами.

7. Что называется скалярным и векторным произведениями двух векторов, каковы их свойства и как эти произведения выражаются через координаты перемножаемых векторов?

8. Что называется смешанным произведением трех векторов, каков геометрический смысл смешанного произведения и как оно выражается через координаты векторов-сомножителей?

9. Выведите формулы преобразования декартовых координат на плоскости.

10. Как определяются полярная, цилиндрическая и сферическая системы координат?

Геометрия на плоскости

1. Как аналитически представляются линии на плоскости? Приведите примеры.

2. Выведите формулы деления отрезка в данном отношении.

3. Как можно найти точку пересечения двух линий на плоскости? Приведите примеры.

4. Что называется угловым коэффициентом прямой на плоскости, каков его геометрический смысл в декартовой прямоугольной системе координат? Как найти угловой коэффициент прямой, если известно ее общее уравнение?

5. Как записываются уравнения прямой, проходящей через две заданные точки?

6. Что называется направляющим вектором прямой на плоскости?

7. Как вычисляются углы между двумя прямыми?

8. Каковы условия параллельности и перпендикулярности двух прямых?

Введение в математический анализ

1. Определение функции. Что называется областью определения функции?

2. Каковы основные способы задания функции? Примеры.

3. Какая функция называется периодической? Примеры.

4. Какие функции называются четными, нечетными? Примеры.

5. Какие функции называются возрастающими, убывающими? Примеры.

6. Какие функции называются элементарными, основными элементарными? Примеры.

7. Какая функция называется сложной? Примеры.

8. Сформулируйте определения предела функции при стремлении аргумента к некоторому конечному пределу и предела функции при стремлении аргумента к бесконечности.

9. Как связаны понятия предела функции с понятиями ее пределов слева и справа?

10. Определение ограниченной функции. Теорема об ограниченности функции, имеющей предел.

11. Какая функция называется бесконечно малой и каковы ее основные свойства?

12. Какая функция называется бесконечно большой, какова ее связь с бесконечно малой?

13. Сформулируйте основные теоремы о пределах функции.

14. Замечательный предел .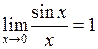

15. Определение непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?

16. Сформулируйте основные свойства непрерывности функций и дайте геометрическое истолкование этим свойствам.

17. Сравнение бесконечно малых. Эквивалентные бесконечно малые.

Производная и дифференциал

1. Сформулируйте определение производной. Каков ее механический и геометрический смысл?

2. Какой класс функций шире: непрерывных или дифференцируемых? Приведите примеры.

3. Выведите формулы производных суммы, произведения, частного двух функций. Приведите примеры.

4. Выведите формулу дифференцирования сложной функции.

5. Запомните таблицу основных формул дифференцирования.

6. Сформулируйте определение дифференциала функции. Каков его геометрический смысл?

7. В чем заключается свойство инвариантности формы дифференциала функции?

8. На чем основано применение дифференциала в приближенных вычислениях?

9. Сформулируйте определение производной высших порядков.

10. Каков механический смысл второй производной?

11. Сформулируйте теорему Ролля. Каков ее геометрический смысл?

12. Сформулируйте теорему Лагранжа. Каков ее геометрический смысл?

13. Сформулируйте правило Лопиталя для раскрытия неопределенностей вида или 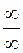. Приведите примеры.

14. Сформулируйте определение возрастающей и убывающей на отрезке функции.

15. Выведите достаточный признак возрастания функции.

16. Сформулируйте определение точки максимума и минимума.

17. Сформулируйте два правила для отыскания экстремумов функции.

18. Приведите пример, доказывающий, что обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума функции.

19. Как найти наименьшее и наибольшее значения функции, дифференцируемой на отрезке? Всегда ли они существуют?

20. Сформулируйте определения выпуклости и выгнутости линии, точки перегиба.

21. Как находятся интервалы выпуклости и вогнутости и точки перегиба линии, заданной уравнением 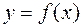? Приведите пример.

22. Сформулируйте определение асимптоты линии.

23. Как находятся вертикальные асимптоты линии, заданной уравнением 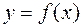? Приведите пример.

24. Как находятся невертикальные асимптоты линии, заданной уравнением 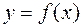? Приведите пример.

25. Изложите схему общего исследования функции и построения ее графика.