Интегралы вида ∫tgmx dx, ∫ctgmx dx

Для нахождения этих интегралов примен. ф-лы, с пом. кот. помлед-но понижается степень m.

tg²x = (1/cos²x) - 1, ctg²x = (1/sin²x) - 1

1/cosx = secx, 1/sinx = cosecx

tg²x = sec²x - 1, ctg²x = cosec²x - 1

Замечание.

Если m-степень частная, то удобно делать подст. tg x = t., тогда x = arctg t.

dx = dt/ (1+t²) и интеграл сводится к интегралу от непр. рацион. дроби.

Интегралы вида ∫ sin mx * cos nx dx, ∫ cos mx * cos nx dx, ∫ sin mx * sin nx dx/

В этом случае примен. след. тригон. функции:

sin mx * cos nx = ½ (sin (m+n) + sin (m-n))

cos mx * cos nx = ½ (cos (m+n) +cos (m-n))

sin mx * sin nx = ½ (cos (m-n) – cos (m+n))

Эти формулы дают нам произведение предс. в виде суммы.

Интегрирование нек. иррациональностей.

Интегралы вида ∫R (x, ^m√ax+b )

Такие интегралы наход. подстановкой ax+b = t^m.

Интегралы вида ∫ ((Mx+N)dx)/((x-α) √ax²+bx+c )

x - α = 1/t

dx = -1/t² dt

Тригонометрические подстановки.

∫R (x, √a²-x² ) dx, ∫R (x, √a²+x² ) dx

Чтобы избавиться от корня и привести интегралы к рацион. тригон. виду, примен. подстановки.

Подстановка для первого: x = a sint (x = a cost)

Подстановка для второго: x = a tgt

Если под знаком Ö содерж. кв. трехчлен, то выделяем полный квадрат.

Существует ряд интегралов, не берущ. в элемент. ф-ях, т.е. для подынтг. ф-и нельзя найти первообразную:

∫(sinx/x) dx - интегральный синус

∫(cosx/x) dx - интегральный косинус

∫е^{-x^2} dx - интеграл вероятности

∫(lnx/x) dx и др.

y = f(x) – непрерывна на отрезке [a;b].

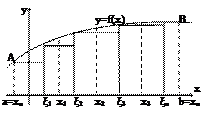
аАВв – криволинейная трапеция.

Вычислим площадь трапеции: Q - ?

Разобьем отр. [a;b] точками на частичный отрезки произ. образом. X₀ = а, х₁,х₂…x_n = b.

Длину каждого их этих отрезков обозначим через Δx_i=(i=1,2,…,n), Δx₁=x₁-x_o, Δx₂=x₂-x₁… Δx_i=x_i-x_i-1

На каждом из частных отрезков построим прямоуг-ки с основаниями DXi с высотой f(ξ_i)

ΔS_i = Δx_i * f(ξ_i), где i=1,2,…,n - площадь каждого из прямоугольников.

Сумма всех площадей:

n   i=1

n   i=1

∑∆S_i ≈ 0 = ∑ f(ξ_i) * ∆S_i

Очевидно тем точнее, чем больше n (мелк. отрезков), т.е. сумма, стоящая слева этого рав-ва назыв. интегральной суммой на отрезке [а;b].

Значение этой суммы зависит как от способа деления отрезка [a,b] на частичные, так и от выбора точек x. Очевидно, точное значение искомой площади мы можем получить, если в рав-ве перейти к пределу при n®¥ или (DXi®0).

Т. обр.

n   i=1

∆xi→0

Q = lim ∑ f(ξ_i) * ∆x_i

b   a

Определение. Если при любых делениях отрезка [а;b] таких, что DXi®0 и при любом выборе точек x_i на этих отрезках, интегральная сумма ® к одному и тому же пределу, то этот предел назыв. опред. интегралом от ф-и y= f(x) на отрезке [a;b] и обозначают ∫ f(x) dx

	b   a

n   i=1

∆xi→0

Т.о. ∫ f(x)dx = lim ∑ f(ξ_i) - ∆x

b   a

Геометрически опред. интеграл – площадь кривол. Трапеции, огран. Сверху ф-ей f(x), прфмыми х=а, х=b и осью ОХ.

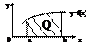
Q = ∫ f(x)dx

Замечание.

Опред. интеграл в отличие от неопред. есть число, зависящее от вида подыинтегр.ф-и, пределов интегр-я, не зависящее от обозн. переменной интегрир-я.

b   a

b   a

Св-ва опред. интеграла.

1. ∫ α * f(x)dx = α * ∫ f(x)dx

	b   a		b   a		b   a		b   a

2. ∫ [ f₁(x) ± f₂(x) ± … ± f_n(x) ] dx = ∫ f₁(x)dx ± ∫ f₂(x)dx ± … ± ∫ f_n(x)dx

b   a

b   a

определенный интеграл от алгебраической суммы конечного числа слагаемых равен такой же сумме интегралов слогаемых.

3. если на отрезке [a,b], (a≤b) φ(x) ≥ f(x), то ∫ φ(x)dx ≥ ∫ f(x)dx

b   a

4. Если m и M соответственно наим. И наиб. Значения ф-и на отрезке [a;b] (а£b), то

m(b-a) £ ∫ f(x)dx £ M(b-a)

5. Теорема о среднем. Если f(x) непрерывна на отрезке, то на этом отрезке найд. такая точка х=с, что быдет выполняться равенство:

	b   a

∫ f(x)dx = f(c) - (b-a)

Эта ф-ла не может быть использвана для вычисления инт-ла из-за неопред. точки "с".

6. Для любых 3-х чисел a,b,c справедливо рав-в

	b   a		b   a		b   c

∫ f(x)dx = ∫ f(x)dx + ∫ f(x)dx

7. Имеет место след. неравенство

	b   a		b   a

│∫ f(x)dx│ ≤ ∫│f(x)│dx

	a   a		b   a		a   b

Замечание: ∫ f(x)dx = 0, ∫ f(x)dx = - ∫ f(x)dx

Теорема 1.

Производная от опред. интеграла по перем. верхнему пределу равна подынт. ф-и:

x   a

∫ f(t)dt = Φ'(x), что Ф'(x) = f(x)