Построение теней конуса и цилиндра
Для построения собственной и падающей теней конуса необходимо провести касательную лучевую поверхность, которая представляет собой две плоскости, касательные к конусу и параллельные световым лучам.
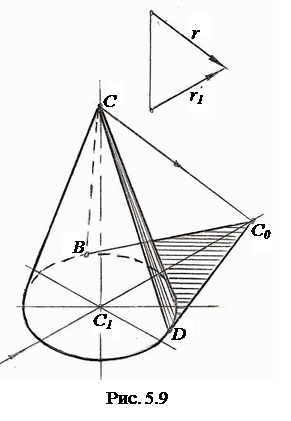
Построение тени от прямого кругового конуса на плоскость его основания в прямоугольной изометрии при заданном направлении световых лучей показано на рис. 5.9.
Для построения контура падающей тени сначала определяют тень C0 от вершины C конуса на плоскость его основания. Затем из точки C0 проводят касательные C0D и C0B к контуру основания конуса, которые и определяют границу падающей тени конуса, а образующие CD и CB конуса отделяют освещённую часть от неосвещённой, то есть составляют границу собственной тени конуса.
 Если конус обращён вершиной вниз (рис. 5.10), то сначала можно построить собственную тень конуса. Для этого из вершины конуса C проведём так называемый обратный луч C
Если конус обращён вершиной вниз (рис. 5.10), то сначала можно построить собственную тень конуса. Для этого из вершины конуса C проведём так называемый обратный луч C 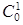 параллельно r до пересечения с плоскостью основания конуса в точке
параллельно r до пересечения с плоскостью основания конуса в точке 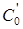 , а затем из точки
, а затем из точки  проведём касательные к основанию конуса в точках B и D. Образующие CB и CD определяют границу собственной тени конуса.
проведём касательные к основанию конуса в точках B и D. Образующие CB и CD определяют границу собственной тени конуса.
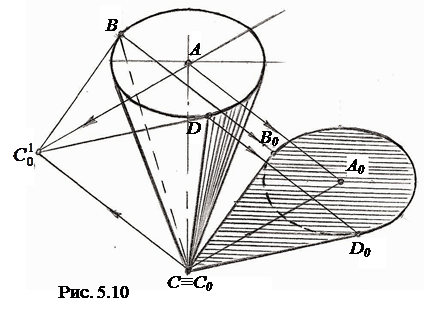 Для построения падающей тени конуса сначала надо построить падающую тень от основания конуса. Для этого можно найти тень A0 от центра A основания конуса и построить эллипс, конгруэнтный (равный) основанию конуса. Этот эллипс можно построить также по точкам. Затем через точки B и D проводим лучи параллельно r и на падающей тени от основания конуса отмечаем точки B0 и D0 , которые соединяем с точкой C≡C0. Полученная фигура будет контуром падающей тени.
Для построения падающей тени конуса сначала надо построить падающую тень от основания конуса. Для этого можно найти тень A0 от центра A основания конуса и построить эллипс, конгруэнтный (равный) основанию конуса. Этот эллипс можно построить также по точкам. Затем через точки B и D проводим лучи параллельно r и на падающей тени от основания конуса отмечаем точки B0 и D0 , которые соединяем с точкой C≡C0. Полученная фигура будет контуром падающей тени.
Для построения собственной и падающей теней цилиндра также необходимо провести касательную лучевую поверхность, которая представляет собой касательные плоскости, параллельные оси цилиндра.
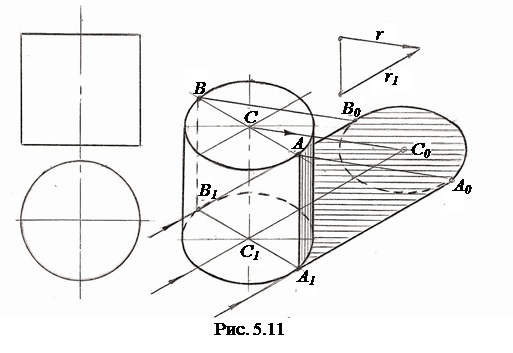
На рис. 5.11 показано построение собственной и падающей теней прямого кругового цилиндра в прямоугольной изометрии.
Световые лучи при заданном направлении r, касаясь боковой поверхности цилиндра, образуют две плоскости, касающиеся цилиндра по двум образующим AA1 и BB1. Следовательно, проведя прямые, касательные к контуру нижнего основания цилиндра параллельно вторичной проекции r1, определим границу собственной тени боковой поверхности - это образующие AA1 и BB1,и границу падающей тени боковой поверхности - это касательные A1A0 и B1B0.
Для построения падающей тени от верхнего основания цилиндра можно найти тень C0 от точки C, а затем построить эллипс, конгруэнтный верхнему основанию, или построить по точкам падающую тень дуги AB -верхней границы собственной тени.