Квадратні рівняння
Квадратні рівняння розглядаються у такій послідовності:
1) вводиться поняття квадратного рівняння за допомогою задачі практичного змісту;
2) дається означення квадратного рівняння;
3) розглядають окремі види квадратних рівнянь.
Задача. Довжина прямокутника більша від його ширини на 3 см., а площа дорівнює 10 см2. Знайти розміри прямокутника?
х – ширина прямокутника;
(х+3) – довжина,
S=х(х+3);
х(х+3)=10 або х2+3х-10=0.
У цьому випадку потрібно розв’язати рівняння, у яких невідома величина у другому степені
Як бачимо, такі рівняння мають практичне значення. Найпростіші з них, а саме за площею квадрата знаходити його сторону, люди вміли розв’язувати ще в Стародавньому Єгипті.
Тому основна мета нашої роботи на уроці – навчитися розв’язувати такі рівняння. Їх називають квадратними.
Означення.Рівняння виду ax2+bx+c=0, де а 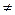 0, х-змінна, називається квадратним.
0, х-змінна, називається квадратним.
Після означення розглядаються окремі види квадратних рівнянь. Учні засвоївши означення квадратного рівняння загального виду, самостійно конструюють означення неповних квадратних рівнянь.
1. b=0; c=0; ax2=0;
2. b=0; c 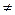 0; ax2+c=0;
0; ax2+c=0;
3. b 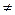 0; c=0; ax2+bx=0;
0; c=0; ax2+bx=0;
4. a 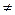 0; b
0; b 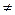 0; c
0; c 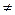 0; ax2+bx+c=0.
0; ax2+bx+c=0.
Корисно підкреслити на уроці відмінність, яка існує між поняттями “квадратне рівняння” і “рівняння другого степеня”.
2х2-3х+5=0 – квадратне рівняння,
2ху+3х+5=0 – рівняння другого степеня відносно змінних х і у,
2х2+ 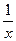 -3=0 – учні вважають квадратним рівнянням, бо воно містить х2.
-3=0 – учні вважають квадратним рівнянням, бо воно містить х2.
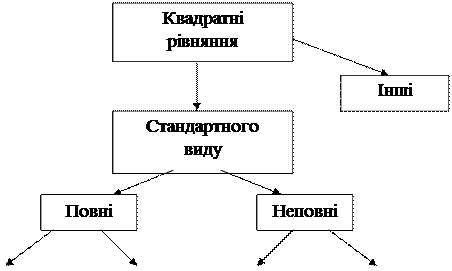
Класифікація квадратних рівнянь
 |
|
|
|
|
Розв’язування квадратних рівнянь бажано починати з неповних: ах2=0; ах2+с=0; ax2+bx=0, а тоді ax2+bx+с=0.
Є такі способи розв’язування квадратних рівнянь:
1) графічний спосіб, з яким учні знайомляться у 9-му класі за підручником Бевза, а в 8-му класі за підручником Макаревича у=ах2 і у=-bх+с.
Абсциси точок перетину графіків цих двох функцій будуть коренями рівняння. Учні повинні розуміти, що залежно від взаємного розміщення параболи і прямої квадратне рівняння може мати корені, або не мати їх.
2) за допомогою виділення повного квадрата двочлена х2-5х+6=0; (х- 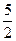 ) 2-
) 2- 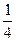 =0; (х-
=0; (х- 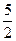 -
- 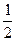 )(х-
)(х- 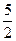 +
+ 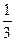 )=0;
)=0;
3) за допомогою коренів квадратного рівняння, яка виводиться різними способами.
