Тема № 3. Физика колебательных процессов
Колебания – это периодическое изменение положения тела или системы относительно некоторого центра равновесия. Это изменение положения характеризуется амплитудой и периодом (частотой) колебаний.
Колебания здания представляют собой суперпозицию собственных и вынужденных колебаний, вызванных различными внутренними (работой бытовой техники и технических систем здания) и внешними (городским транспортом, стройками, ветровым воздействием и сейсмической активностью) воздействиями. В таблице 3.1 приведены значения периодов собственных колебаний зданий в зависимости от вида ограждающих конструкций.
Таблица 3.1 – Период собственных колебаний зданий по горизонтальным осям
| Число этажей | Период, с | ||
| Крупнопанельные здания | Крупноблочные и кирпичные здания | Каркасные здания | |
| 0,18-0,27 0,36-0,57 0,46-0,74 0,56-0,91 0,66-1,09 0,76-1,26 | 0,22-0,35 0,39-0,61 0,47-0,77 0,56-0,93 0,64-1,09 0,73-1,25 | 0,26-0,42 0,61-0,93 0,81-1,22 1,01-1,51 1,21-1,81 1,41-2,10 |
При совпадении частот собственных и внешних колебаний возникает резонанс, что может привести к разрушению конструкции отдельных частей здания или сооружения в целом.
При свободных затухающих колебаниях на систему действуют две силы: сила, заставляющая систему совершать колебания, и сила сопротивления среды. Сопротивление среды характеризуется коэффициентомсопротивления, который влияет на затухание колебаний. Поэтому все колебания, возникающие в строениях, являются затухающими.
На площадках, сейсмичность которых превышает 9 баллов, возводить здания и сооружения, как правило, не допускается. При необходимости строительство на таких площадках ведется при обязательном научном сопровождении и участии специализированной научно-исследовательской организации. Проектирование зданий высотой более 75 м и сооружений с пролетами более 50 м также должно осуществляться при участии таких организаций.
Колебания зданий и сооружений могут быть горизонтальными и вертикальными, а также крутильными относительно вертикальной оси. Колебания любого типа подчиняются теории колебательного движения и его законам.
Задание 3.1. Материальная точка совершает гармонические колебания согласно уравнению х=0,02cos(πt+π/2) м. Определить амплитуду, период и начальную фазу колебаний, максимальные скорость и ускорение точки, а также значение времени после начала отсчета, когда точка будет проходить через положение равновесия.
Решение. Уравнение гармонических колебаний имеет вид
х=Аcos(ωоt+φ),
где А – амплитуда колебаний, м;
ωо – собственная частота колебаний, рад/с;
t – время колебаний, с;
φ – начальная фаза колебаний, рад.
Период колебаний и собственная частота связаны между собой соотношением
Т=2π/ωо.
С помощью данных выражений получено: амплитуда колебаний равна 0,02 м, начальная фаза – π/2, период – 2 с.
Скорость колебаний определяется как первая производная координаты по времени, ускорение – как вторая производная. Отсюда следует
υ=-0,02πsin(πt+π/2)
и
a=-0,02π2cos(πt+π/2).
Данные величины принимают максимальные значения при равенстве единице тригонометрических функций, следовательно,
υmax=0,02π м/с
и
amax=0,02π2 м/с2.
При определении времени прохождения точки через положение равновесия после начала отсчета необходимо приравнять координату к нулю и решить тригонометрическое уравнение
0,02cos(πt+π/2)=0.
В данном случае время определяется набором натуральных чисел, которые показывают значения времени в секундах после начала колебаний, когда точка будет проходить через положение равновесия, то есть 0, 1, 2, 3, 4 и так далее.
Ответ: А=0,02 м, φ=π/2, Т=2 с, υmax=0,0628 м/с, amax=0,197 м/с2,
t=0, 1, 2, 3, 4, …, с.
Таблица 3.2 – Задание 3.1 по вариантам
| № варианта | Уравнение гармонических колебаний, м |
| х=0,2cos(πt+π) | |
| х=cos(πt+π/4) | |
| х=2cos(πt+π/3) | |
| х=0,04cos(2πt+π/6) | |
| х=0,8cos(5πt) | |
| х=cos(2πt) | |
| х=0,25cos(4πt+π/2) | |
| х=0,5cos(5πt+π/4) | |
| х=cos(πt+π/2) | |
| х=0,1cos(πt) |
Задание 3.2. Тело массой 10 г совершает гармонические колебания по закону х=0,1cos(4πt+π/4) м. Определить максимальные значения возвращающей силы и кинетической энергии.
Решение. Уравнение гармонических колебаний имеет вид
х=Аcos(ωоt+φ),
Скорость колебаний определяется как первая производная координаты по времени, ускорение – как вторая производная. Отсюда следует
υ=-0,4πsin(4πt+π/4)
и
a=-1,6π2cos(4πt+π/4).
Максимальные значения возвращающей силы и кинетической энергии будут определяться через максимальные значения скорости и ускорения
υmax=0,4π м/с
и
amax=1,6π2 м/с2.
Максимальное значение возвращающей силы
Fmax=mamax.
Максимальное значение кинетической энергии
Ekmax=mυ2max/2.
Расчеты дают следующие значения Fmax=0,158 Н, Ekmax=7,89 мДж.
Ответ: Fmax=0,158 Н, Ekmax=7,89 мДж.
Таблица 3.3 – Задание 3.2 по вариантам
| № варианта | Масса тела, г | Уравнение гармонических колебаний, м |
| х=0,2cos(πt+π) | ||
| х=cos(t+π/4) | ||
| х=2cos(t+π/3) | ||
| х=0,04cos(2πt+π/6) | ||
| х=0,8cos(5πt) | ||
| х=cos(2πt) | ||
| х=0,25cos(4πt+π/2) | ||
| х=0,5cos(5πt+π/4) | ||
| х=cos(t+π/2) | ||
| х=0,1cos(πt) |
Задание 3.3. Материальная точка массой 20 г совершает гармонические колебания по закону х=0,1cos(4πt+π/4) м. Определить полную энергию этой точки.
Решение. Уравнение гармонических колебаний имеет вид
х=Аcos(ωоt+φ).
Полная энергия точки определяется как сумма кинетической Ек и потенциальной Еп энергий. Кинетическая энергия будет вычисляться по формуле
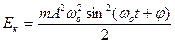 .
.
Потенциальная энергия – по формуле
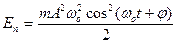 .
.
Полная энергия точки
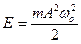 .
.
После вычисления получается значение 15,8 мДж.
Ответ: Е=15,8 мДж.
Таблица 3.4 – Задание 3.3 по вариантам
| № варианта | Масса тела, г | Уравнение гармонических колебаний, м |
| х=0,2cos(πt+π) | ||
| х=cos(t+π/4) | ||
| х=2cos(t+π/3) | ||
| х=0,04cos(2πt+π/6) | ||
| х=0,8cos(5πt) | ||
| х=cos(2πt) | ||
| х=0,25cos(4πt+π/2) | ||
| х=0,5cos(5πt+π/4) | ||
| х=cos(t+π/2) | ||
| х=0,1cos(πt) |
Задание 3.4. Материальная точка совершает гармонические колебания с амплитудой 5 см и собственной частотой колебаний π/12 рад/с без начальной фазы. Когда возвращающаяся сила в первый раз достигает значения -12 мН, потенциальная энергия точки оказывается равной 0,15 мДж. Определить этот момент времени.
Решение. Уравнение колебаний в этом случае имеет вид х=0,05cos(πt/12) м. Возвращающая сила определяется по формуле
F=-kx=-Akcosωt,
где k – коэффициент упругости, Н/м.
Потенциальная энергия вычисляется по формуле
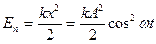 .
.
Взяв отношение потенциальной энергии к силе, получим
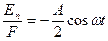 .
.
Из данного равенства выражается время
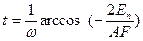 .
.
После вычисления получим искомое значение времени 4 с.
Ответ: t=4 с.
Таблица 3.5 – Задание 3.4 по вариантам
| № варианта | Амплитуда, см | Собственная частота колебаний, рад/с | Возвращающаяся сила, мН | Потенциальная энергия, мДж |
| π/2 | -5 | 0,15 | ||
| π/3 | -10 | |||
| π/4 | -15 | 0,5 | ||
| π/6 | -20 | 0,25 | ||
| π/3 | -10 | 0,75 | ||
| π/2 | -20 | 0,2 | ||
| π/4 | -25 | 0,4 | ||
| π/6 | -5 | 0,5 | ||
| π/12 | -12 | |||
| π/2 | -10 | 0,5 |
Задание 3.5. На горизонтальной пружине жесткостью k=900 Н/м укреплен шар массой М=4 кг, лежащий на гладком столе, по которому он может скользить без трения. Пуля массой m=10 г, летящая с горизонтальной скоростью υо=600 м/с и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определить амплитуду и период колебаний шара.
Решение. Скорость υ движения системы шар-пуля определяется из закона сохранения импульса
mυo=(M+m) υ,
таким образом,
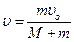 .
.
Амплитуда колебаний находится из закона сохранения энергии
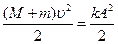
или
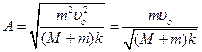 .
.
Ответ: А=0,1 м.
Таблица 3.6 – Задание 3.5 по вариантам
| № варианта | Жесткость пружины, Н/м | Масса шара, кг | Масса пули, г | Скорость пули,м/с |
Задание 3.6. Складываются два гармонических колебания одного направления, описываемых уравнениями x1=3cos2πt, x2=3cos(2πt+π/4) см. Определить для результирующего колебания амплитуду и начальную фазу колебаний. Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд.
Решение. Уравнение гармонических колебаний имеет вид
х=Аcos(ωоt+φ).
Следовательно, собственная частота каждого колебания равна 2π рад/с, амплитуда по 3 см, начальная фаза первого колебаний φ1=0, второго – φ2=π/4.
Амплитуда результирующего колебания определяется по формуле
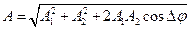 ,
,
где Δφ=φ2-φ1 – разность фаз. Амплитуда равна 5,54 см.
Фаза результирующего колебания определяется согласно выражению
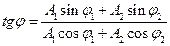 .
.
После вычисления получается число π/8. Уравнение результирующего колебания будет иметь вид
х=5,54cos(2πt+π/8) см.
Векторная диаграмма сложения амплитуд представлена на рисунке 3.1.
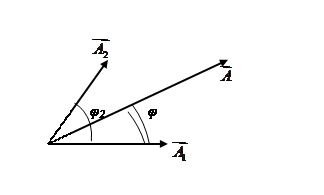
Рисунок 3.1 – Векторная диаграмма сложения амплитуд
Таблица 3.7 – Задание 3.6 по вариантам
| № варианта | Уравнение первого колебания, см | Уравнение второго колебания, м |
| cost | 0,01cos(t+π/2) | |
| 2cosπt | 0,02cos(πt+π/3) | |
| 3cosπt | 0,03cos(πt+π/3) | |
| 4cos2πt | 0,04cos(2πt+π/4) | |
| 5cost | 0,05cos(t+π) | |
| 6cost | 0,06cost | |
| 7cosπt | 0,07cos(πt+π/4) | |
| 8cosπt | 0,08cos(πt+π/3) | |
| 9cos2πt | 0,09cos(2πt+π/6) | |
| cost | 0,01cos(t+π/6) |
Задание 3.7. Результирующее колебание, получающееся при сложении двух гармонических колебаний одного направления, описывается уравнением х=Аcostcos45t, время в секундах. Определить циклические частоты складываемых колебаний и период биения результирующего колебания.
Решение. Координата результирующего колебания в этом случае определяется по формуле
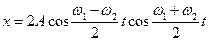 ,
,
где ω1 и ω2 – собственные частоты складывающихся колебаний;
А – амплитуда колебания.
Из данного равенства следует
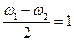
и
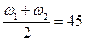 .
.
После вычислений получается, что ω1=46 рад/с и ω2=44 рад/с.
Период биения вычисляется по формуле
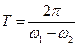 ,
,
что дает величину, равную 3,14 с.
Ответ: ω1=46 рад/с, ω2=44 рад/с, Т=3,14 с.
Таблица 3.8 – Задание 3.7 по вариантам
| № варианта | Уравнение гармонического колебания, м |
| х=0,5Аcostcos10t | |
| х=2Аcos2tcos20t | |
| х=Аcos5tcos25t | |
| х=2Аcos10tcos30t | |
| х=Аcos10tcos40t | |
| х=Аcos20tcos50t | |
| х=3Аcos5tcos55t | |
| х=Аcos20tcos60t | |
| х=4Аcos20tcos70t | |
| х=Аcos30tcos80t |
Задание 3.8. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x=3cos2ωt и y=4cos(2ωt+π), см. Определить уравнение траектории точки и начертить ее с нанесением масштаба.
Решение. Выполним некоторые преобразования в уравнениях колебания:
y=-4cos2ωt,
cos2ωt=-y/4,
cos2ωt=x/3,
-y/4=x/3,
y=(-4/3)x.
Получившееся равенство представляет собой прямую линию, график которой представлен на рисунке 3.2.
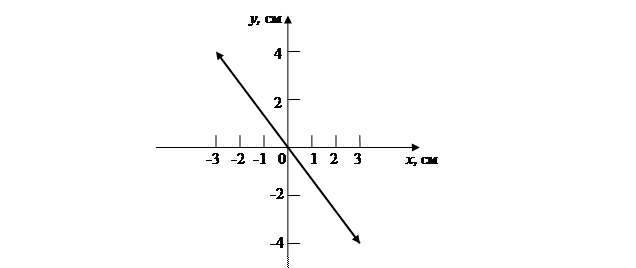
Рисунок 3.2 – График траектории точки
Таблица 3.9 – Задание 3.8 по вариантам
| № варианта | Уравнение первого колебания, см | Уравнение второго колебания, см |
| x=cosωt | y=4cos(ωt+π) | |
| x=3cosωt | y=6cos(ωt+π) | |
| x=2cos2ωt | y=8cos(2ωt+π) | |
| x=5cos3ωt | y=10cos(3ωt+π) | |
| x=10cos4ωt | y=10cos(4ωt+π) | |
| x=8cos2ωt | y=24cos(2ωt+π) | |
| x=12cos6ωt | y=36cos(6ωt+π) | |
| x=15cos8ωt | y=5cos(8ωt+π) | |
| x=20cos2ωt | y=4cos(2ωt+π) | |
| x=5cosωt | y=5cos(ωt+π) |
Задание 3.9. Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x=Asin(ωt+π/2), y=Asinωt. Определить уравнение траектории точки и начертить ее с нанесением масштаба. Определить направление движения точки по траектории.
Решение. Выполним некоторые преобразования в уравнениях колебания:
х=Acosωt,
x2+y2=A2cos2ωt+A2sin2ωt,
x2+y2=A2.
Последнее уравнение представляет собой окружность с центром в начале координат и радиусом, равном амплитуде А. Если подставить значения времени в уравнения движения по осям x и y, можно получить направление движение точки. В данном случае против часовой стрелки. Траектория движения представлена на рисунке 3.3.
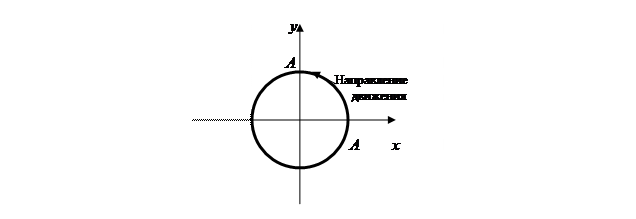
Рисунок 3.3 – Траектория движения точки
Таблица 3.10 – Задание 3.9 по вариантам
| № варианта | Уравнение первого колебания, м | Уравнение второго колебания, м |
| x=Acos(ωt-2π) | y=Asinωt | |
| x=0,5Asin(ωt+π/2) | y=0,5Asinωt | |
| x=Acos(ωt) | y=Asinωt | |
| x=4Asin(ωt+π/2) | y=4Asinωt | |
| x=5Asinωt | y=5Asin(ωt+π/2) | |
| x=0,1Asin(ωt+π/2) | y=0,1Asinωt | |
| x=Asinωt | y=Acosωt | |
| x=0,1Asinωt | y=0,1Asin(ωt+π/2) | |
| x=3Asinωt | y=3Acosωt | |
| x=A2 sin(ωt+π/2) | y=A2 sinωt |
Задание 3.10. Тело массой m=100 г, совершая затухающие колебания, за время τ=1 мин потеряло 40 % своей энергии. Определить коэффициент сопротивления r.
Решение. Коэффициент сопротивления определяется через коэффициент δ затухания при механических колебаниях
δ=r/2m.
Энергия колебаний определяется по формуле
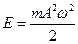 .
.
Амплитуда колебаний изменяется согласно закону
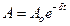 ,
,
где Ао – начальная амплитуда колебаний.
Напишем отношение энергий колебаний в начальный момент времени к энергии колебаний через время τ=1 мин и получим коэффициент затухания
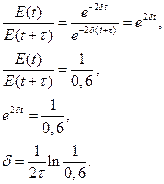
Учитывая полученное выражение, найдем коэффициент сопротивления
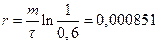 .
.
Ответ: r=8,51.10-4 кг/с.
Таблица 3.11 – Задание 3.10 по вариантам
| № варианта | Масса тела, г | Время | Потери энергии, % |
| 20 с | |||
| 25 с | |||
| 30 с | |||
| 40 с | |||
| 50 с | |||
| 1 мин | |||
| 1,5 мин | |||
| 2 мин | |||
| 2 мин 10 с | |||
| 2 мин 25 с |
Задание 3.11. Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуды первого и шестого колебаний А1/А6=13. Определить резонансную частоту данной колебательной системы.
Решение. Амплитуда затухающих колебаний определяется через начальную амплитуду Ао и коэффициент δ затухания
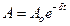 .
.
Отношение амплитуд получается равным
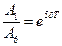 .
.
Из этого соотношения найдем коэффициент затухания
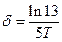 .
.
Угловая резонансная частота ωрез и угловая частота ω колебаний определяются через собственную угловую частоту ωо колебаний, период Т колебаний и коэффициент затухания
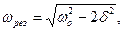
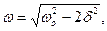
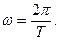
Искомая резонансная частота колебательной системы равна
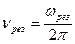 .
.
Вычисления по приведенным формулам дают величину 4,98 Гц.
Ответ: νрез=4,98 Гц.
Таблица 3.12 – Задание 3.11 по вариантам
