Изучение работы конденсатора

1 Квазистационарные токи

2 Дифференциальные уравнения для RC-цепи

3 Зависимость тока зарядки и разрядки конденсатора от времени

Основные понятия по теме

Если подключить конденсатор к источнику постоянного тока (рисунок 8.1), то напряжение на нем U_c экспоненциально возрастает, асимптотически стремясь к ЭДС источника. При этом сила тока I (направление тока указано на рисунке 8.1), проходящего через сопротивление R, убывает по экспоненте, уменьшаясь до нуля.

Процесс зарядки конденсатора можно описать с помощью закона Ома для полной цепи:

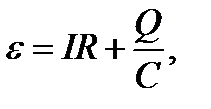(8.1)

согласно которому сторонняя ЭДС равна сумме падений напряжения на всех участках цепи (внутренним сопротивлением источника пренебрегаем). В выражении (8.1) учтено, что напряжение U_c на обкладках конденсатора связано с зарядом Q соотношением U_c = Q/C , где С – емкость конденсатора.

- +

Е

I

R

C

1 K 2

Рисунок 8.1 – Принципиальная схема заряда и разряда конденсатора

Дифференцируя (8.1) по времени и принимая во внимание, что сила тока равна скорости изменения заряда на обкладках

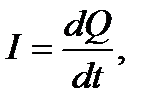
получаем дифференциальное уравнение с разделяющимися переменными

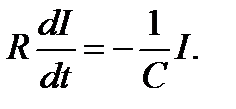(8.2)

Решение уравнения (8.2) имеет вид:

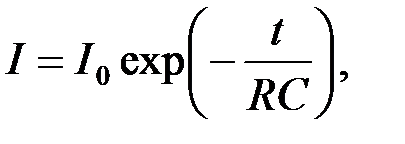(8.3)

где постоянная интегрирования I₀ , равная силе тока в момент времени t = 0, может быть определена из начальных условий. Поскольку в начальный момент времени Q = 0, (заряд на обкладках не успел накопиться), то из (8.1) следует:

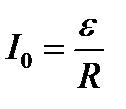
. (8.4)

При разрядке конденсатора соответственно справедливы соотношения

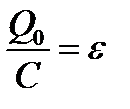
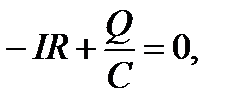
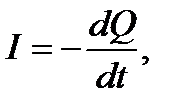
(направление тока изменилось на противоположное, происходит уменьшение заряда на обкладках, начальное напряжение на конденсаторе равно ЭДС источника). В результате зависимость силы тока от времени остается неизменной.

Из уравнения (8.3) находим закон изменения напряжения U_R на сопротивлении R и напряжения на конденсаторе U_C(рисунок 8.2):

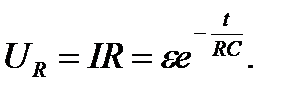
(8.5)

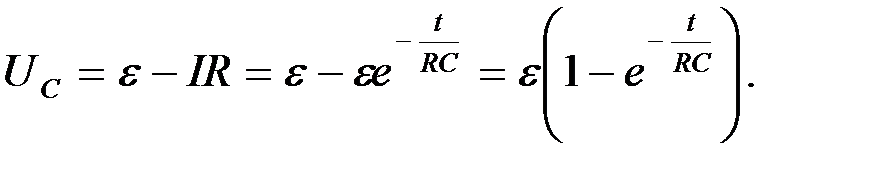
(8.6)

а)

б)

I

t

0,368I0

t

UR

t

UC

U

ε

t

0.63ε

Рисунок 8.2 – а) зависимость силы тока в цепи от времени;

б) изменение напряжения U_R на сопротивлении R в зависимости

от времени; изменение напряжения на емкости U_C в зависимости

от времени (осциллограмма)

Для характеристики средней скорости изменения силы тока в цепи при зарядке и разрядке конденсатора вводится в рассмотрение время релаксации системы:

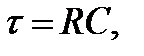(8.7)

в течение которого сила тока уменьшается в е раз, т. е. сила тока при t = t составляет 0,368 от максимального значения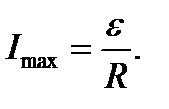

Формула зависимости силы тока I и напряжений U_R и U_C от времени при разрядке конденсатора через сопротивление R при отключенном источнике тока находится из уравнения U_С = IR. Студентам самим предоставляется возможность выполнить решение этой задачи и убедиться в том, что U_С , I и U_R при разрядке конденсатора изменяются по одному и тому же закону: ~exp(-t/RC). Если прологарифмировать выражение (8.3), получаем:

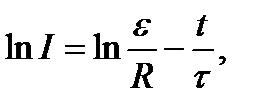
(8.8)

то есть изменение логарифма силы тока прямо пропорционально времени. При этом угловой коэффициент прямой, графически выражающий зависимость lnI = f(t), связан со временем релаксации обратной зависимостью tga = 1/t. Точка пересечения прямой с осью ординат дает значение логарифма начальной силы тока (рисунок 8.3).

t

ln I

ln I0

a

Рисунок 8.3 – Определение времени релаксации

из графика lnI = f(t)

На практике часто используется параллельное или последовательное соединение конденсаторов. Емкость нескольких параллельно соединенных конденсаторов равна сумме их емкостей:

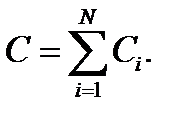
В случае последовательного соединения конденсаторов справедлива такая же формула, как при параллельном соединении резисторов:

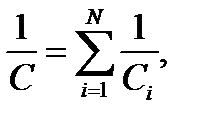
где N – количество соединенных конденсаторов.

Вопросы для самоконтроля

1 Что такое квазистационарные токи.

2 Запишите дифференциальные уравнения для RC-цепи.

3 Поясните зависимость тока зарядки и разрядки конденсатора от времени.

4 Как определить t цепи из осциллограммы.

5 Рассчитайте емкости при параллельном и последовательном соединении конденсаторов.

6 Поясните осциллограммы зарядки-разрядки конденсатора, приведенные на рисунке 8.5.

Лабораторная работа 8

Изучение процессов зарядки и разрядки конденсатора

Цель работы: усвоение понятия об электрической емкости, изучение процессов зарядки и разрядки конденсатора осциллографическим методом, определение времени релаксации процесса и емкости конденсатора.

Приборы и принадлежности: кассета ФПЭ–ПИ/09, магазин сопротивлений (2 шт), магазин емкостей, источник питания, генератор низкочастотный, осциллограф С1-117.

Описание установки

Работа выполняется по схеме, приведенной на рисунке 8.4.

R2

C

Y

“PO”

R1

ГЗ 102

ФПЭ ПИ/09 “PQ”

Рисунок 8.4 – Блок-схема установки

С низкочастотного генератора синусоидальный сигнал подается на кассету ПИ, с выхода которой прямоугольные импульсы через два магазина сопротивлений подаются на магазин емкостей. Для того, чтобы получить осциллограммы зарядки и разрядки конденсатора, необходимо через постоянные промежутки времени подключать конденсатор к цепи и сразу же его отключать. Причем частота переключения должна быть такой, при которой незаметно было бы мерцание изображения на экране. Роль такого переключателя в данной работе выполняют прямоугольные импульсы, получаемые с помощью кассеты ФПЭ-ПИ/09 или непосредственно с выхода генератора, поскольку большинство генераторов имеют синусоидальный и прямоугольный выходной сигналы.

Синусоидальный сигнал (1–3 В) подается от входных гнезд Х1, Х2 через разделительный конденсатор С1 на компаратор напряжения (микросхема серии К554СА3Б). Выходной сигнал компаратора управляется усилительным каскадом. С выходных гнезд Х3, Х4 снимается сигнал прямоугольной формы положительной полярности с амплитудой 11,5 В.

Ход работы

1 Используя рисунок 8.4, соберите рабочую схему. Подключите к разъему кассеты ФПЭ-ПИ/09 кабель источника питания.