Геометрическая интерпретация
Условились комплексное число z = a + bi изображать точкой плоскости с координатами (a; b). Действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа - точками оси ординат, которую называют мнимой осью.
Каждой точке плоскости с координатами ( a ; b ) соответствует вектор с началом в точке О ( 0 ; 0 ) и концом в точке М ( a ; b ). Поэтому комплексное число a + bi можно изображать в виде вектора 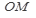 .
.
Такое изображение комплексных чисел особенно широко применяется в технических дисциплинах.
Из геометрической интерпретации комплексного числа вытекает:
1. Длина вектора, изображающего комплексное число, равна модулю комплексного числа: 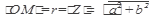
2. Угол 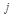 между вектором, изображающим комплексное число, и положительным направлением оси Ох называется аргументом комплексного числа
между вектором, изображающим комплексное число, и положительным направлением оси Ох называется аргументом комплексного числа 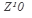 :
: 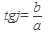
Если Z = 0, то аргумент не определен.
3.Из соотношений между сторонами углами прямоугольного треугольника
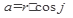 ,
, 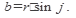
Тогда, используя параметры 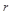 и
и 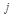 можно записать:
можно записать: 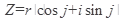 - тригонометрическая формула записи комплексного числа.
- тригонометрическая формула записи комплексного числа.
Действия над комплексными числами в тригонометрической форме:
1. 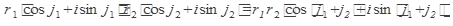 ;
;
2. 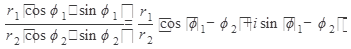 ;
;
3. 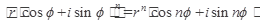 ;
;
4. 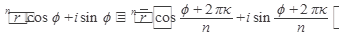 ,где k = 0, 1, 2, ..., n-1.
,где k = 0, 1, 2, ..., n-1.
Те же параметры 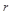 и
и 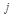 при использовании формулы Эйлера :
при использовании формулы Эйлера :
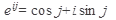 дают более компактную запись:
дают более компактную запись: 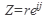 - показательная форма записи комплексного числа.
- показательная форма записи комплексного числа.
Действия над комплексными числами в показательной форме:
1. 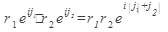 ;
;
2. 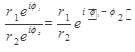 ;
;
3. 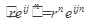 ;
;
4. 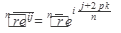 , где k = 0, 1, 2, ..., n - 1.
, где k = 0, 1, 2, ..., n - 1.
На практике тригонометрическая форма используется как переходная:
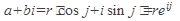
Часто бывает так, что два комплексных числа, над которыми надо произвести то или иное действие, заданы в различных формах. Поэтому сначала их надо привести к одной и той же форме.
Для перевода комплексного числа из алгебраической формы в тригонометрическую или показательную необходимо:
1. Найти модуль комплексного числа 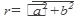 ;
;
2. Найти аргумент комплексного числа 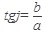 ;
;
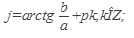
определив в какой четверти расположен изображающий комплексное число вектор, выбрать нужное значение аргумента.
Для перевода комплексного числа из показательной или тригонометрической формы в алгебраическую. Следует воспользоваться формулами приведения и значениями углов тригонометрических функций.
Пример 1. Перемножить два комплексных числа 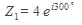 и
и  в алгебраической и показательной форме.
в алгебраической и показательной форме.
Решение: Для выполнения действия в алгебраической форме переведем Z1 сначала в тригонометрическую, а затем в алгебраическую форму:
Z1 = 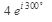 =4(cos3000 + i sin3000) =4( cos(2700 + 300) +
=4(cos3000 + i sin3000) =4( cos(2700 + 300) +
+ i sin(2700 + 300))= 4(sin300 - i cos300) = 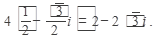
Перемножим сомножители по правилу умножения двучлена на двучлен:
Z1 Z2 = 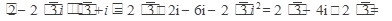
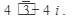
Теперь выполним действия в показательной форме, для чего Z2 переведем из алгебраической формы в показательную:

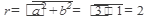
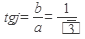
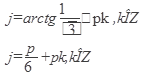
Так как вектор изображающий комплексное число 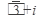 , расположен в первой четверти, то выбираем К = 0, тогда
, расположен в первой четверти, то выбираем К = 0, тогда 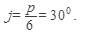
Получаем 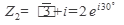
Найдем произведение: 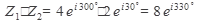
Ответ: 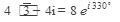
Пример 2. Вычислить 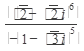 . Ответ записать в алгебраической, тригонометрической, показательной формах.
. Ответ записать в алгебраической, тригонометрической, показательной формах.
Решение: Основания степеней даны в алгебраической форме. Так как возведение в степень проще производить в показательной форме, то сначала выполним перевод комплексных чисел в показательную форму.
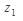 =
= 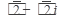
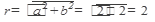
tg 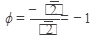
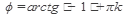 , k
, k 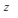
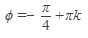 ,k
,k 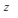
Так как вектор, изображающий комплексное число 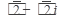 расположен в четвертой четверти, то выбираем К = 0, тогда
расположен в четвертой четверти, то выбираем К = 0, тогда 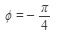
Получаем 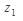 =
= 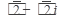 =
= 
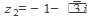
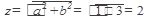
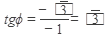
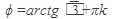 ,k
,k  z
z
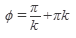 ,k
,k 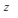
Так как вектор, изображающий комплексное число 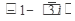 , расположен в третьей четверти, то выбираем К = 1, тогда
, расположен в третьей четверти, то выбираем К = 1, тогда 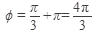
Получаем 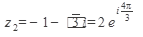
Выполнили возведение в степень
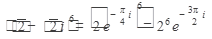
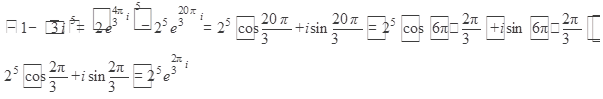
Выполнили деление

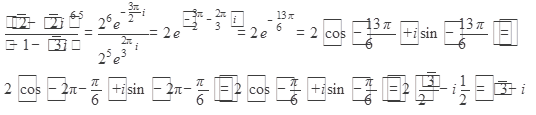
Ответ:
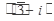 -алгебраическая форма
-алгебраическая форма
 - тригонометрическая форма
- тригонометрическая форма
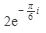 - показательная форма.
- показательная форма.
Пример 3. Вычислить  , ответ записать в алгебраической, тригонометрической и показательной формах.
, ответ записать в алгебраической, тригонометрической и показательной формах.
Решение: Надо произвести действия над комплексными числами, заданными в различных формах. Поэтому сначала их надо привести к одной форме. Так как возведение в степень проще производить в показательной форме, то сначала комплексное число 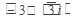 переведем в показательную форму.
переведем в показательную форму.
Z= 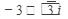
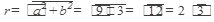
tg 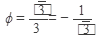
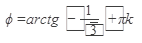 ,k
,k 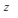
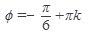 ,k
,k 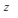
Так как вектор, изображающий комплексное число 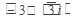 , расположен во второй четверти, то выбираем К = 1, тогда
, расположен во второй четверти, то выбираем К = 1, тогда
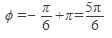
Выполним возведение в степень
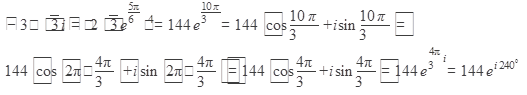
Найдем произведение
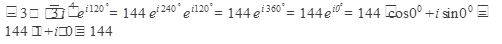
Ответ:
144-алгебраическая форма
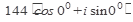 - тригонометрическая форма
- тригонометрическая форма
144е 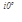 -показательная форма
-показательная форма
Предел функций
Определение 1.
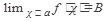
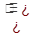 " E>0 $ б=б(Е)>0 "cÎД
" E>0 $ б=б(Е)>0 "cÎД
0< çх-а½< бÞçf(x)-Bç<E
Определение 2.
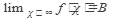
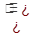 " E>0 $ М>0 "cÎД
" E>0 $ М>0 "cÎД
çх ½>МÞçf(x)-Bç<E
Условие существования предела:
{$ 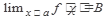 }Û
}Û 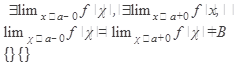
Теоремы о пределах
Пусть существуют lim f(x) и lim g(x), тогда:
Теорема 1
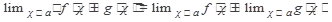
Теорема 2
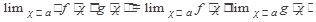
Следствие:
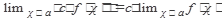 , где с=const
, где с=const
Теорема 3
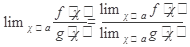 , где
, где 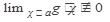
Теорема 4. Если 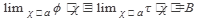 и в некоторой окрестности точки а, кроме быть может самой точки а, выполнено неравенство
и в некоторой окрестности точки а, кроме быть может самой точки а, выполнено неравенство 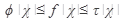 , то
, то 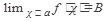
Пример 1. Вычислить 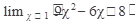
Решение: воспользуемся теоремами о пределах
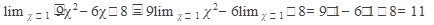
Ответ: 11
Пример 2. Вычислить 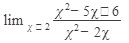
Решение: в этом примере пределы числителя и знаменателя при х =>2 равны нулю:
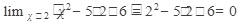
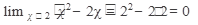
Следовательно, теорему о пределе частного применять нельзя.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и следовательно, сделать возможным применение теоремы 3.
Квадратный трехчлен в числителе разложим по формуле ax2 + bx + c = a(x - x1)(x - x2), где х1 и х2 - корни трехчлена. Разложив на множители и знаменатель, сократим дробь на (х - 2), затем применем теорему 3.
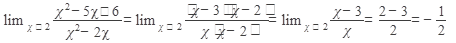
Ответ: 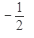
Пример 3. Вычислить 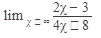
Решение: При 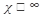 числитель и знаменатель стремятся к бесконечности, поэтому при непосредственном применении теоремы 3 получаем выражение
числитель и знаменатель стремятся к бесконечности, поэтому при непосредственном применении теоремы 3 получаем выражение 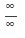 , которое представляет собой неопределенность. Для избавления от неопределенности такого вида следует разделить числитель и знаменатель на старшую степень аргумента. В данном примере нужно разделить на х:
, которое представляет собой неопределенность. Для избавления от неопределенности такого вида следует разделить числитель и знаменатель на старшую степень аргумента. В данном примере нужно разделить на х: 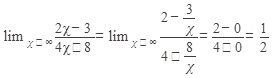
Ответ: 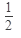
Пример 4. Вычислить 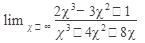
Решение: при 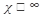 . числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т. е. на х3:
. числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т. е. на х3:
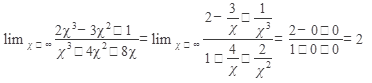
Ответ: 2
Пример 5. Вычислить 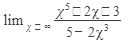
Решение: При 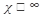 числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на высшую степень аргумента, т.е. на х5:
числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на высшую степень аргумента, т.е. на х5:
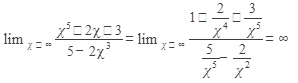
числитель дроби стремится к 1, знаменатель к 0, поэтому дробь стремится к бесконечности.
Ответ:¥
Пример 6. Вычислить 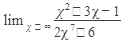
Решение: при х 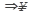 числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. на х7:
числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. на х7:
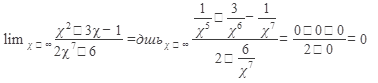
Ответ: 0.
Производная функции
Определение 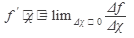
Производные основных элементарных функций:
1. (const)’=0 2. (x n)’= nx n - 1 3. (a x)¢=ax lna 4. (e x)¢=ex 5.(log a x)’= 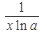 6.(ln x)’= 6.(ln x)’= 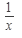 | 7(sin x)’= cos x 8(cos x)’= -sin x 9(tg x)’= 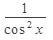 10(ctg x)’= 10(ctg x)’= 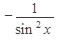 11.(arcsinx)’= 11.(arcsinx)’= 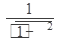 12.(arccosx)¢= 12.(arccosx)¢= 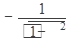 13.(arctg x)’= 13.(arctg x)’= 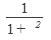 14.(arcctgx)’= 14.(arcctgx)’= 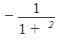 |
Правила нахождения дифференцирования:
а) 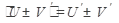
б) 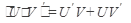
в) 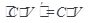 ,где С=const
,где С=const
г) 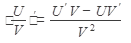
д) 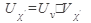 ,где U=U(V(x)) сложная функция
,где U=U(V(x)) сложная функция
Пример 1.Найти производную функции 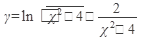
Решение: Если производную от второго слагаемого находим по правилу дифференцирования дроби, то первое слагаемое представляет собой сложную функцию, производная которой находится по формуле:
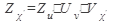 , где
, где 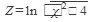 ,
, 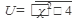 ,V=x2 +4
,V=x2 +4
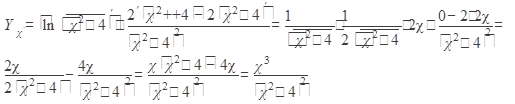
При решении были использованы формулы: 1, 2,6, а, г, д.
Ответ: 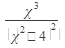
Пример 2.Найти производную функции 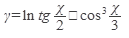
Решение: оба слагаемых - сложные функции, где для первого
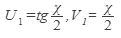 , а для второго
, а для второго 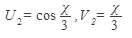
Тогда
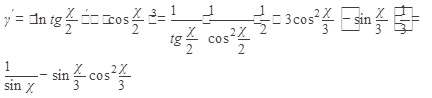
При решении были использованы формулы 2,6,8,9,а,в,д и формулы Тригонометрии
Ответ: 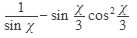
Определенный интеграл.
Формулы интегрирования:
1) 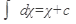 2) 2) 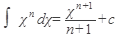 ,где n¹1 3) ,где n¹1 3) 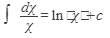 4) 4) 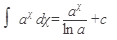 5) 5) 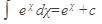 6) 6) 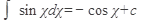 7) 7) 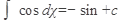 | 8) 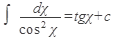 9) 9) 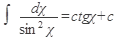 10) 10) 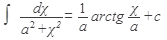 11) 11) 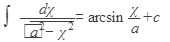 12) 12) 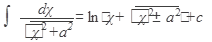 13) 13) 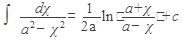 |
Формула Ньютона-Лейбница:
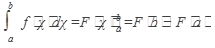
Основные свойства определенного интеграла:
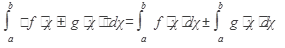
1.
2. 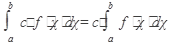 , с=const
, с=const
3. 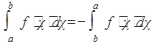
Интегрирование методом замены переменной:
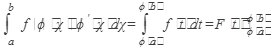
Интеграл с помощью подстановки 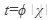 преобразуется в другой (обычно табличный) интеграл с новой переменной интегрирования t, где старые пределы интегрирования х1 = а; х2 = b заменяются новыми пределами
преобразуется в другой (обычно табличный) интеграл с новой переменной интегрирования t, где старые пределы интегрирования х1 = а; х2 = b заменяются новыми пределами 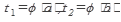
Пример 1. Вычислить 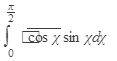
Решение: положим t = cos x, тогда dt = (cos x)’dx = -sin xdx или sin xdx = -dt;
вычислим пределы интегрирования для переменной t: t1 = cos 0 = 1, t2 = 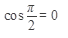
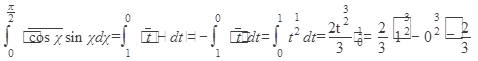
Ответ: 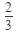
Пример 2. Вычислить 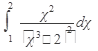
Решение: произведем подстановку 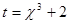 , тогда
, тогда
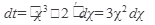 или
или 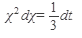
Определим новые пределы интегрирования:
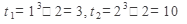
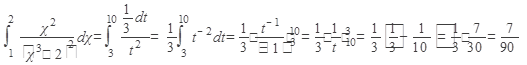
Ответ: 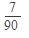
Дифференциальные уравнения.
Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.
Порядком дифференциального уравнения называется наивысший порядок производной неизвестной функции, входящей в уравнение.
Решением дифференциального уравнения называется функция
y =f(x),
подстановка которой в уравнение обращает его в тождество. График решения на плоскости хОу называется интегральной кривой уравнения.
Дифференциальные уравнения первого порядка часто записывают в виде: y’ = f(x;y) или dy = f(x;y)dx. Простейшее дифференциальное уравнение первого порядка есть уравнение y’ = f(x), где f(x)- заданная функция.
Это уравнение имеет бесконечно много решений.
Процесс нахождения решения называется интегрированием дифференциального уравнения. Поэтому для y’ = f(x), функция 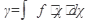 или
или 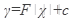 где F(x) какая-нибудь первообразная функция f(x), а с - произвольная постоянная, будет общим решением (общим интегралом).
где F(x) какая-нибудь первообразная функция f(x), а с - произвольная постоянная, будет общим решением (общим интегралом).
Чтобы выделить единственное решение уравнения, достаточно задать значение искомой функции при фиксированном значении аргумента. Задача нахождения решения дифференциального уравнения первого порядка, удовлетворяющего условию y(x0) = y0, где x0 и у0 - заданные числа, называется задачей Коши.
Условие у(х0) = у0 называется начальным условием, а единственное решение, удовлетворяющее начальному условию, называется частным решением уравнения (частным интегралом).
Частное решение уравнения с физической точки зрения означает, что в фиксированный (начальный) момент времени задано положение материальной точки, а геометрический смысл состоит в нахождении интегральной кривой уравнения, проходящей через заданную точку.
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно привести к виду y’=f(x)g(y). Уравнение этого вида решается с помощью разделения переменных 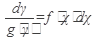 и интегрирования обеих частей полученного уравнения по своей переменной.
и интегрирования обеих частей полученного уравнения по своей переменной.
Пример 1. Найти частное решение дифференциального уравнения
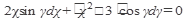 ,если
,если 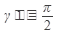
Решение: имеем уравнение с разделяющимися переменными.
Разделим переменные, разделив каждый член уравнения на произведение (x2+3)sin y:
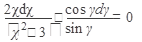
проинтегрируем обе части уравнения
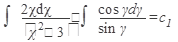
интегралы вычислим методом подстановки
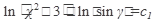
для удобства преобразований примем c1=ln c,
тогда имеем 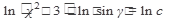
после потенцирования получаем общее решение:
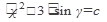
Подставив начальное условие, находим С
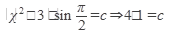
Подставляя найденное значение С в общее решение получаем частное решение.
Ответ: частное решение уравнения (частный интеграл)
 или
или 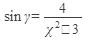
Пример 2.Найти частное решение дифференциального уравнения y2dx= 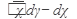 , если у(0)=1.
, если у(0)=1.
Решение: соберем члены содержащие dx и dy в разных частях уравнения, а затем разделим переменные:
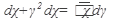
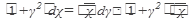
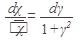
интегрированием найдем общее решение:
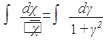
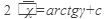
подставив начальное условие, находим С
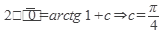
При найденном значении С из общего интеграла найдем частное решение (частный интеграл) данного уравнения:
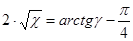
Ответ: частное решение 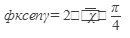
Ряды
Определение 1.Числовым рядом называется выражение вида
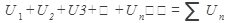 , где числа
, где числа 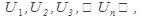 называемые членами ряда, образуют бесконечную последовательность.
называемые членами ряда, образуют бесконечную последовательность.
Определение 2. Ряд называется сходящимся, если последовательность его частичных сумм 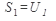
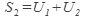
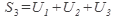
. . . . . . . . . . . . . .
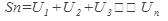
при 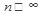 имеет конечный предел :
имеет конечный предел : 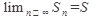
Этот предел называется суммой ряда. Если же 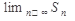 не существует или бесконечен, то ряд называется расходящимся.
не существует или бесконечен, то ряд называется расходящимся.
Необходимый признак сходимости ряда.
Если ряд сходится, то его общий член стремится к нулю, т.е 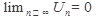
Признак Коши. Если для ряда с положительными членами 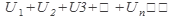 величина
величина 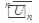 при
при 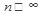 имеет конечный предел l , т.е
имеет конечный предел l , т.е 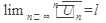 ,то : 1)в случае l<1 ряд сходится; 2)в случае l>1 ряд расходится;
,то : 1)в случае l<1 ряд сходится; 2)в случае l>1 ряд расходится;
Примечание. Если l=1, то ряд может как сходится, так и расходится.
Признак Даламбера. Если для ряда с положительными членами 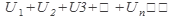 отношение (n+1)-го члена к n-му при
отношение (n+1)-го члена к n-му при 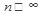 имеет конечный предел l, т.е
имеет конечный предел l, т.е 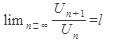 , то : 1) в случае l<1 ряд сходится; 2)в случае l>1 ряд расходится.
, то : 1) в случае l<1 ряд сходится; 2)в случае l>1 ряд расходится.
Примечание. Если l= 1, то ряд может как сходится, так и расходится.
Пример1исследовать на сходимость ряд

Решение: ряд расходится, т.к 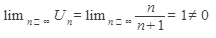 (не выполнен необходимый признак сходимости).
(не выполнен необходимый признак сходимости).
Пример 2. Исследовать на сходимость ряд 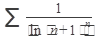
Решение: Воспользуемся признаком Каши.
Находим 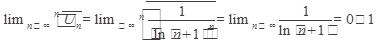 ; следовательно, ряд сходится.
; следовательно, ряд сходится.
Пример 3. Исследовать на сходимость ряд
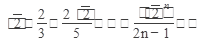
Решение : Так как 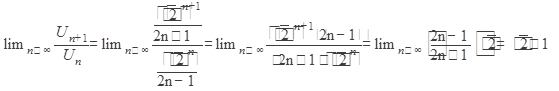 , то данный ряд расходится по признаку Даламбера.
, то данный ряд расходится по признаку Даламбера.
Элементы теории вероятностей
При вычислении вероятностей случайных событий часто приходится использовать формулы комбинаторики. Комбинаторными называются задачи, в которых требуется произвести подсчет всех составленных по некоторому правилу соединений из некоторого числа различных предметов (элементов).
Различают три типа соединений:
1. Перестановки - соединения, отличающиеся только порядком следования элементов при их неизменном числе. Общее число перестановок из n элементов обозначается Pn. Это число равно произведению всех натуральных чисел от 1 до n включительно:
Pn= 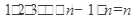 !
!
Символ n ! (читается: эн факториал) есть сокращенное обозначение произведения 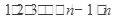
Пример 1. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4 без повторения цифр?
Решение: так как искомые соединения содержат все по четыре данных элемента и отличаются друг от друга только порядком следования элементов, то это перестановки, общее число которых:
P4=4!= 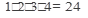 (Для данного примера можно перебрать все эти варианты:
(Для данного примера можно перебрать все эти варианты:
1234, 1243, 1324, 1342, 1423, 1432, и т.д.)
Ответ: 24
2. Размещения - соединения элементов, которые отличаются или порядком элементов в соединении, или самими элементами. Общее число размещений из n элементов по m элементов обозначается 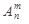 , где
, где 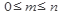 и вычисляется по формуле
и вычисляется по формуле 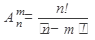
Пример 2. Сколько двузначных чисел можно составить из цифр 1, 2, 3, 4 без повторения цифр?
Решение: так как искомые соединения содержат по два элемента из данных четырех элементов и отличаются друг от друга или порядком следования элементов, или самими элементами, то это размещения, общее число которых: 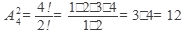 (Для данного примера перечислим все возможные варианты: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43)
(Для данного примера перечислим все возможные варианты: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43)
Ответ:12
3. Сочетания - соединения, отличающиеся друг от друга хотя бы одним элементом. В отличие от размещений в сочетаниях порядок следования элементов не имеет значения. Общее число сочетаний из n элементов по m элементов обозначается 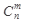 , где
, где 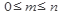 и вычисляется по формуле:
и вычисляется по формуле: 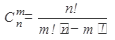
Пример 3.На 6 сотрудников выделены 3 одинаковые путевки в дом отдыха. Сколькими способами их можно распределить?
Решение: так как путевки одинаковые, то число способов их распределения равно числу сочетаний из 6 элементов по 3 элемента.
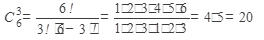
Ответ: 20
Теория вероятностей - математическая наука, которая изучает закономерность в случайных событиях. К основным понятиям теории вероятностей относятся испытания и события.
Под вероятностью случайного события понимают численную меру объективной возможности появления этого события.
Вероятностью Р(А) случайного события А называется отношение числа m исходов, благоприятствующих событию А к числу n-всех элементарных исходов. Формула 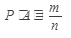 называется классическим определением вероятности.
называется классическим определением вероятности.
Для невозможного события P(V)=0 , для достоверного события P(U)=1 . Отсюда вероятность случайного события 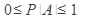
Пример 4. Из 20 лотерейных билетов 3 выигрышных. Какова вероятность того, что из двух наугад взятых билетов оба выигрышные.
Решение: Из 20 билетов выбрать 2 можно
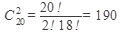 способами,
способами,
а благоприятствующих исходов 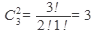
Тогда 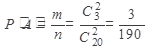
Ответ: 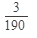
Пример 5. В ящике 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение:
Событие А – извлеченные детали окрашены
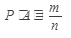
n - число возможных исходов
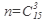 ,
,
m - число благоприятствующих исходов
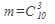 ,
,
Тогда 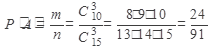
Ответ: 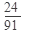
Пример 6. В урне 15 красных и 5 синих шаров. Вынули 4 шара. Какова вероятность, что два вынутых шара красные, а два синие?
Решение: 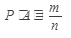
число возможных исходов n= 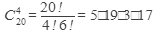
Два красных шара могут быть выбраны  способами, а два синих
способами, а два синих 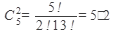 способами.
способами.
Тогда благоприятствующих исходов 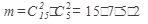
Искомая вероятность 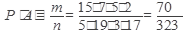
Ответ: 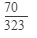
Пример 7. Карточка «Спортлото» содержит 45 чисел. В тираже участвуют 6 чисел. Какова вероятность того, что верно будут угаданы 5 чисел?
Решение: 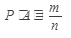 ,где
,где
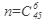 , а
, а 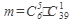
где 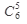 -выбраны 5 из 6 участвующих в тираже чисел,
-выбраны 5 из 6 участвующих в тираже чисел,
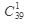 -названо одно из 39 невыигрышных чисел (39=45-6)
-названо одно из 39 невыигрышных чисел (39=45-6)
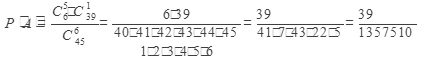
Ответ: 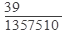
Задания для контрольной работы.
Студент должен выполнить пять заданий того варианта, номер которого совпадает с последней цифрой его шифра
| Вариант | Задания | ||||||
| 1 | 2 | 3 | 4 | 5 | |||
| а | б | а | б | ||||
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
Задание 1.
Выполнить действия в показательной форме. Ответ записать в тригонометрической и алгебраической форме.
1. 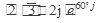
2. 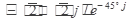
3. 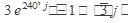
4. 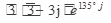
5. 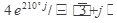
6. 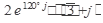
7. 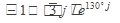
8. 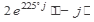
9. 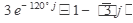
10. 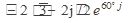
Задание 2.
а)Вычислить:
11. 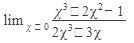 12. 12. 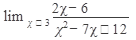 13. 13. 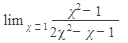 14. 14. 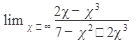 15. 15. 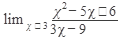 | 16. 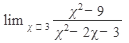 17. 17. 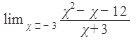 18. 18. 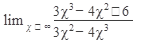 19. 19. 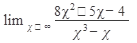 20. 20. 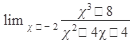 |
б) Найти производную функции:
21. 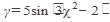 22. 22. 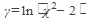 23. 23. 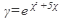 24. 24. 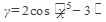 25. 25. 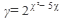 | 26. 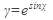 27. 27. 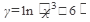 28. 28. 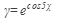 29. 29. 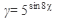 30. 30. 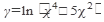 |
Задание 3.
Вычислить:
а) Найти общее решение дифференциального уравнения:
31. 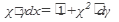 32. 32. 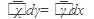 33. 33. 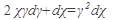 34. 34. 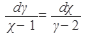 35. 35. 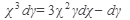 | 36. 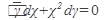 37. 37. 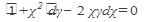 38. 38. 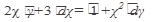 39. 39. 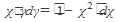 40. 40. 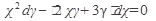 |
б) вычислить
41. 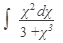 42. 42. 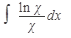 43. 43. 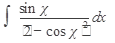 44. 44. 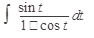 45. 45. 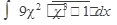 | 46. 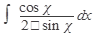 47. 47. 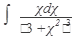 48. 48. 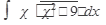 49. 49. 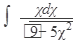 50. 50. 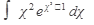 |
Задание 4.
Исследовать ряд на сходимость:
51. 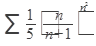 52. 52. 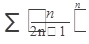 53. 53. 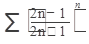 54. 54. 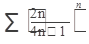  55. 55. 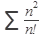 | 56. 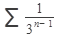 57. 57. 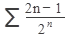 58. 58. 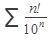 59. 59. 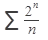 60. 60. 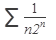 |
Задание 5.
Решить задачу:
61. Карточка «Спортлото» содержит 36 чисел. В тираже участвуют 5 чисел .Какова вероятность того, что верно будет угадано 3 числа?
62. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент ответит правильно на 3 вопроса экзаменатора.
63. В урне находится 7 красных и 6 синих шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара красные?
64. В урне 6 белых и 9 черных шаров. Из урны вынимают одновременно 2 шара. Какова вероятность того, что оба шара окажутся черными?
65. Из 20 лотерейных билетов 3 выигрышных. Какова вероятность того, что из 2 наугад выбранных билетов оба выигрышные?
66. Экзаменационные билеты пронумерованы от 1 до 35. Какова вероятность того, что наугад выбранный билет номер кратный 5?
67. Талоны, свернутые в трубочку пронумерованы всеми двузначными цифрами. Наудачу берут один талон. Какова вероятность того, что номер взятого талона состоит из одинаковых цифр?
68. В урне 3 белых, 7 красных и 5 синих шаров. Какова вероятность того, что вынутые наугад 3 шара окажутся синими?
69. Из m числа шаров, пронумерованных всеми двузначными числам, наудачу берется один. Какова вероятность того, что номер взятого шара оканчивается нулем?
70. Студент выучил 30 вопросов из 40. Какова вероятность того, что ему попадется билет с выученными вопросами, если в билете 3 вопроса?
Вопросы для подготовки к экзамену
1. Понятие комплексного числа.. Геометрическая интерпретация комплексного числа.
2. Алгебраическая, тригонометрическая, показательная формы комплексного числа. Переход от одной формы к другой.
3. Действия над комплексными числами в различных формах..
4. Понятие предела функции. Теоремы о пределах.
5. Правила вычисления пределов рациональных и иррациональных функций.(раскрытие неопределенностей: 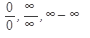 )
)
6. Замечательные пределы.
7. Понятие производной, формулы дифференцирования.
8. Неопределенный интеграл, его свойства. Формулы интегрирования.
9. Определенный интеграл, его свойства. Формула Ньютона-Лейбница.
10. Методы интегрирования подстановкой и «по частям» в неопределенном и определенном интервалах.
11. Дифференциальные уравнения. Задача Коши.
12. Дифференциальные уравнения с разделяющимися переменными.
13. Линейные дифференциальные уравнения 1 порядка.
14. Простейшие дифференциальные уравнения 2 порядка.
15. Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.
16. Числовые ряды, свойства ,признаки сравнения.
17. Знакоположительные ряды. Признаки сходимости Даламбера, Коши.
18. Знакочередующие ряды. Признак Лейбница.
19. Степенные ряды Радиус и интервал сходимости.
20. Ряды Тейлора, Маклорена.
21. Ряд Фурье.
22. Элементы комбинаторики.
23. Понятие вероятности события. Классическое определение вероятности. Операции над событиями.
24. Классификация событий. Теоремы сложения и умножения вероятностей.
25. Полная группа событий. Формула полной вероятности, формула Байеса.
26. Повторение испытаний. Формула Бернулли.
27. Дискретные случайные величин, способы задания
28. Непрерывные случайные величины, способы задания.
29. Числовые характеристики случайных величин.
30. Числовые методы.
Литература
1. Алгебра и начала анализа, ч.1,2, под ред. Г.Н.Яковлева. -М.: Наука, 1981.
2. И.Л.Зайцев. Элементы высшей математики для техникумов. -М.: Наука, 1974.
3. Д.Письменный конспект лекций по высшей математике.
4. Н.В.Богомолов. Практические занятия по математике. -М.: Высшая школа, 2002.
5. В.Е.Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. -М.: Высшая школа, 1979.
6. М.Я.Выгодский. Справочник по высшей математике. -М.:Росткнига,2001.
