Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности
• Чем выше корреляция, тем выше дисперсии и больше риск получить несостоятельные оценки. В этом случае говорят о мульти-сти.
• Высокая коррелированность не всегда ведет к несостоятельности. Например если n велико и дисперсия случайного члена мала, то можно получить состоятельные оценки.
• Любая регрессия страдает от мульти-сти. Задача определить, когда это влияние становится существенным
Наибольшие затруднения в использовании аппарата множественной регрессии возникают при наличии мульти-сти факторных переменных, когда более чем два фактора связаны между собой линейной зависимостью.
Мульти-стью для линейной множественной регрессии называется наличие линейной зависимости между факторными переменными, включёнными в модель.
Мульти-сть - нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии.
Мульти-сть в матричном виде - это зависимость между столбцами матрицы факторных переменных Х:
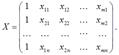
Если не учитывать единичный вектор, то размерность данной матрицы равна n*n. Если ранг матрицы Х меньше n, то в модели присутствует полная или строгая мульти-сть. Но на практике полная мульти-сть почти не встречается.
Можно сделать вывод, что одной из основных причин присутствия мультик-сти в модели множественной регрессии является плохая матрица факторных переменных Х.
Чем сильнее мульти-сть факторных переменных, тем менее надежной является оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.
Включение в модель мульти-ных факторов нежелательно по нескольким причинам:
1) основная гипотеза о незначимости коэффициентов множественной регрессии может подтвердиться, но сама модель регрессии при проверке с помощью F-критерия оказывается значимой, что говорит о завышенной величине коэффициента множественной корреляции;
2) полученные оценки коэффициентов модели множественной регрессии могут быть неоправданно завышены или иметь неправильные знаки;
3) добавление или исключение из исходных данных одного-двух наблюдений оказывает сильное влияние на оценки коэффициентов модели;
4) мульти-ные факторы, включённые в модель множественной регрессии, способны сделать её непригодной для дальнейшего применения.
Конкретных методов обнаружения мульти-сти не существует, а принято применять ряд эмпирических приёмов. В большинстве случаев множественный регрессионный анализ начинается с рассмотрения корреляционной матрицы факторных переменных R или матрицы (ХТХ).
Корреляционной матрицей факторных переменных называется симметричная относительно главной диагонали матрица линейных коэффициентов парной корреляции факторных переменных:

где rij – линейный коэффициент парной корреляции между i-м и j-ым факторными переменными,
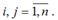
На диагонали корреляционной матрицы находятся единицы, потому что коэффициент корреляции факторной переменной с самой собой равен единице.
При рассмотрении данной матрицы с целью выявления мульти-ных факторов руководствуются следующими признаками:
1) если в корреляционной матрице факторных переменных присутствуют коэффициенты парной корреляции по абсолютной величине большие 0,8, то делают вывод, что в данной модели множественной регрессии существует мульти-сть;
2) вычисляют собственные числа корреляционной матрицы факторных переменных и max. Если min‹10-5, то в модели регрессии присутствует мульти-сть. Если отношение
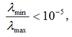
то также делают вывод о наличии мульти-ных факторных переменных;
3) вычисляют определитель корреляционной матрицы факторных переменных. Если его величина очень мала, то в модели регрессии присутствует мульти-сть.
