Точки отсчета

Общий закон продольных перемещений 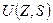тонкостенного стержня, имеющего в поперечном сечении открытый профиль, записывается таким образом [1]:

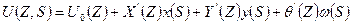(5)

Здесь первыми тремя членами выражен закон плоских сечений, сог­ласно которому поперечные сечения, плоские до деформации, остаются плоскими и после деформации. Продольные перемещения, определяемые этими членами, возникают в результате сложной деформации растяжения в направлении оси и изгиба в двух плоскостях: и . Функция 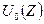определяет осевую деформацию, поперечные сечения при этой деформации получают только поступательные смещения вдоль образующей стержня. Функция 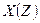и 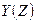, представляют собой прогибы оси стержня в плоскостях 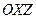, , 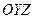характеризуют деформацию изгиба. При этой деформации поперечные сечения, оставаясь плоскими, поворачиваются относительно осей , .

Четвертым членом формулы (5) определяется та часть перемещений, которая не следует закону плоских сечений и возникает в результате кручения. Это отклонение от закона плоских сечений называется секториальной депланацией сечения. Величина 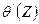, представляющая собой относительный угол кручения, служит мерой депланации стержня при кручении. Характер депланации поперечного сечения из своей плоскости задается функцией 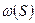, которая называется секториальной площадью.

В классической теории изгиба балок, основанной на законе плоских сечений (три первых члена выражения (5)) за ось стержня принимается линия центров тяжести поперечных сечений стержня. Сам стержень отождествляется с этой осью. Это основное понятие строительной механики стержневых систем, вытекающее из закона плоских сечений и имеющее основание в принципе Сен-Венана.

Для тонкостенного стержня существенно значение имеет также и линия центров тяжести. Линией центров изгиба называется прямая, параллельная оси стержня и обладающая следующим свойством: если внешняя поперечная нагрузка, включая реакции, проходит через эту прямую, то стержень будет находиться в условиях центрального поперечного изгиба. То есть стержень будет находиться в условия закона плоских сечений и его напряженно деформированное состояние описывается первыми тремя членами выражения (5).

Если поперечная нагрузка, включая опорные реакции, хотя бы на одном участке стержня не проходит через линию центров изгиба, то стержень будет испытывать деформацию кручения. В его сечениях возникнут напряжения изгибного кручения, определяемые законом секториальных площадей, которому соответствует четвертый член выражения (5).

Эта линия совпадает с осью центров тяжести сечения для стержней, имеющих в поперечном сечении две оси симметрии. В остальных случаях линия центров изгиба не совпадает с осью стержня.

Таким образом, если вся внешняя нагрузка, включая реакции опор, проходит через центры изгиба поперечных сечений стержня, то он рассчитывается по обычным формулам сопротивления материалов. Если нет, то в сечениях стержня появляются дополнительные напряжения, а сам расчет резко усложняется. Однако понятна практическая значимость информации о положении центра изгиба сечения.

Переходим к изложению методики нахождения координат центра изгиба.

Секториальной площадью 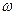называется геометрическая характеристика поперечного сечения, определяемая выражением

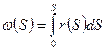, (6)

где 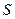- длина элемента контура от некоторой начальной точки отсчета 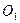на нем до точки, в которой определяется значение секториальной площади: 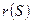- расстояние от полюса 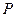до касательной к элементарному отрезку контура 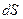. Порядок выбора полюса 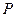и начальной точки отсчета 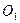будет рассмотрен ниже. Построение эпюры секториальной площади выполняют двигаясь по дуге контуру сечения, откладывая величину 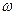по нормали к контуру. Единица измерения - .

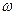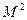Вид эпюры секториальных площадей зависит от положения полюса точки отсчета. Знак эпюры выбирается следующим образом: при обходе контура относительно полюса против часовой стрелки берется знак 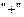, при обходе контура по часовой стрелке – знак .

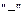Для определения координат центра изгиба строится вспомогательная эпюра 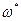, для которой полюс 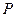стараются выбрать так, чтобы эпюра 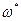на возможно большей части контура была нулевой. Это может быть достигнуто расположением полюса 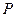в угловых точках сечения или в точках ветвления контура. Выбор начальной точки 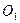преследует те же цели.

На рис. 14, 15 изображены эпюры секторильной площади при различном выборе начальной точки .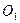

Из этих эпюр видно, что во втором случае положение начальной точки отсчета выбрано неудачо. В качестве эпюры 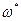поэтому берем эпюру, изображенную на рис.14. В дальнейшем при построении эпюр секториальных площадей будем иметь в виду следующее:

1. На прямолинейных участках профильной линии секториальные площади всегда представляются прямолинейными в общем случае трапецеидальными эпюрами. Поэтому значение секториальной площади вычисляется для начальной и конечной точки прямолинейного участка профиля.

2. Если конец радиуса-вектора скользит по прямой, на которой находится полюс, то секториальная площадь остается не измененной.

3. Начальную точку 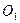следует брать в любой точке прямолинейного отрезка контура, содержащего полю.

4. В случае разветвляющегося контура построение эпюры секториальных площадей ведется с заходом в каждую ветвь и возвращением к точке разветвления.

После построения эпюры 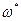координаты центра изгиба определяются выражениями [1], [3]

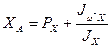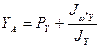; (7)

где 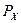, 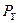- координаты полюса 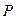, , 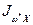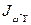называются секторильными центробежными моментами инерции и определяются следующими выражениями:

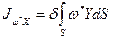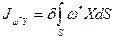; (8)

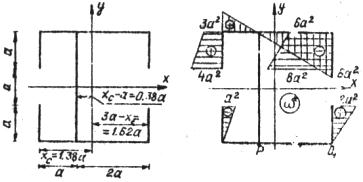
Рис. 14

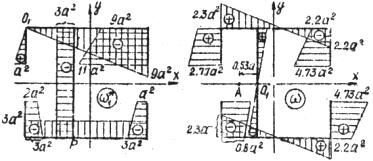
Рис.15 Рис.16

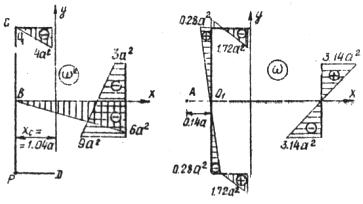
Рис.17 Рис.18

Используя правило Верещагина, вычисляем величины:

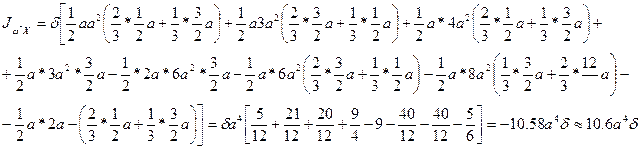
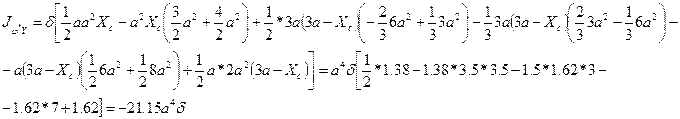Вычисляем величины 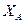и :

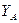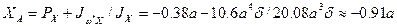
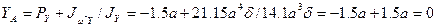
Известно, что центр изгиба при наличии оси симметрии всегда лежит на ней, поэтому степень отличия величины 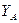от нуля свидетельствует о величине погрешности, допущенной при проведении построений и вычислений. Будем считать допустимым, если величина 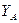находится в пределах

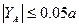(9)

Найденное значение координаты 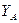удовлетворяет условию (9). Выполнение этого условия означает, что эпюра 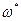построено верно, а величины 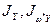определено правильно.

Отметим, что выбранная величина ограничения (9) является “мягким” ограничением. Превышение свидетельствует о недопустимых погрешностях при вычислениях или при построении эпюр. Например, округлив значении 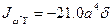, получим

.

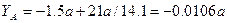Положив 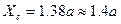, , 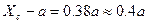, 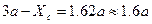получим 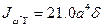и .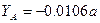

Проверка правильности нахождения координаты 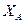осуществляется следующим образом. В начале дадим некоторые определения.

Начальная точка отсчета, для которой при расположении полюса в центре изгиба получаем 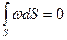, называется главной нулевой секториальной точкой или главной начальной точкой отсчета. Сама величина 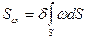называется секториальным статическим моментом.

Для определения положения этой точки имеется специальная методика, однако в случае сечения, имеющего ось симметрии, известно, что этой точкой является ближайшая к центру изгиба точка пересечения оси симметрии с контуром сечения.

На рис.16 показано положение главной нулевой секториальной точки 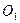. Построим эпюру 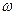для полюса 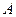с вычисленными координатами 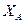, 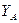и главной начальной точкой отсчета 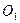- рис.16. Полагая, что точка 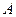является произвольно выбранным полюсом, вычисляем величину 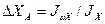. Эта величина дает отрезок, который надо отложить от 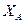в направлении оси , чтобы получить центр изгиба.

Будем считать, что при выполнении условия

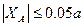(10)

координата 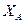центра изгиба определена верно. Одновременно тем самым проверяется правильность построения эпюры .

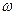Для рассматриваемого примера получаем:

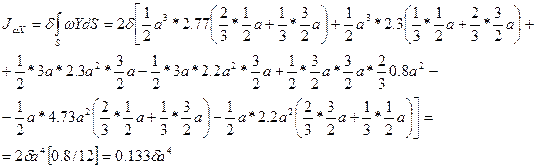
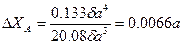. (11)

Таким образом, проверка выполнена.

Для дальнейших вычислений потребуется величина

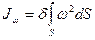, (12)

Которая называется секториальным моментом инерции. При нашем выборе полюса и начальной точки отсчета из четырех геометрических величин, характеризующих сопротивление стержня искривлениям (депланациям) его поперечного сечения в процессе стесненного кручения, три величины обращаться в ноль:

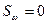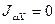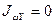, , (13)

Таким образом, секториальный момент инерции 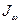остается единственной секториальной характеристикой, характеризующей сопротивляемость тонкостенного стержня искривлениями поперечных сечения из их плоскости. Определяем величину :

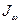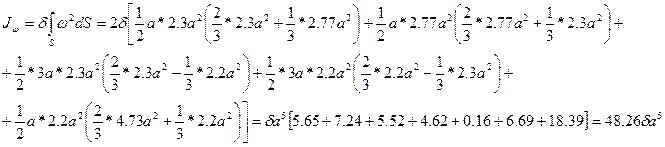
Выше говорилось, что для сечений, имеющих ось симметрии, положение главной нулевой секториальной точки заранее известно. Известно также, что центр изгиба находится на оси симметрии.

Однако при выполнении данной расчетно-проектировочной работы использовать эти сведения при выборе полюса, то есть располагать его на оси симметрии. Подчеркнем, что одной из целей выполнения работы является осознание студентом факта расположения центра изгиба на оси симметрии и методики его нахождения в общем случае для несимметричного поперечного сечения тонкостенного стержня открытого профиля.

Для лучшего усвоения данной методики найдем и построим эпюру 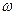для сечения, изображенного на рис. 13.

Одно из возможных положений полюса Р с учетом того, что на оси симметрии брать его при выполнении работы не рекомендуется, показано на рис. 17. За начальную точку 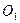выбирается любая точка отрезка 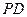или 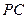. В этом случае для выбранного полюса Р вид эпюры 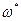получается наиболее простым.

Используя правило Верещагина, получим:

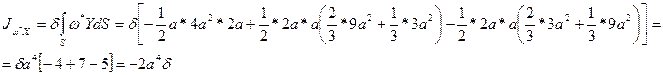
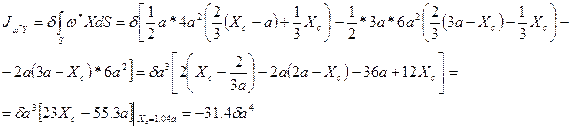
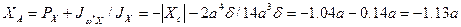
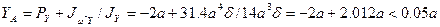
Напомним, что эпюры 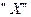и 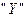берутся на рис.13. Положение центра изгиба 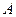, главной нулевой секториальной точки и эпюра 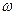приведены на рис.18.

Проводим проверки:

.

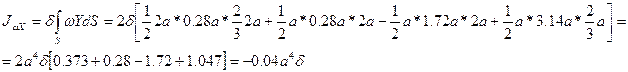
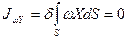
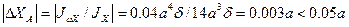
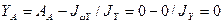Проверки эпюры 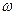и положения центра изгиба выполнены.