Теорема 1. Егер және евклидтік кеңістіктері гомеоморфты болса, онда .

Бұл (Брауэр) теореманы біз дәлелдеусіз қабылдаймыз.

Көпбейненің мысалдарын келтірелік.

1-мысал. 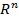кеңістігі 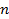-өлшемді көпбейне. 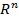-дегі әрбір ашық жиын да 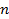-өлшемді көпбейне болады.

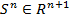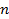2-мысал. сфера -өлшемді көпбейне. Ол 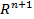кеңістігінің ішкі кеңістігі ретінде саналымды базисі бар хаусдорфты кеңістік болады. Егер 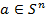және 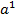-оған диаметральді нүкте болса, онда 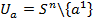маңайы 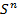-ге 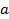нүктесіндегі жанама 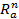жазықтыққа гомеоморфты болады. 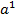нүктесінен центрлі проекциялау арқылы гомеоморфизм орната аламыз.

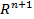-дегі 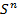сфераның диаметральді қарама-қарсы нүктелерін желімдеу арқылы алынатын 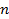-өлшемді проективтік 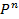кеңістіктің моделі де белгілі.

3-мысал. Проективтік 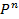кеңістікте 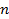-өлшемді топологиялық көпбейне болады. 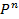-нің әрбір нүктеснің, яғни 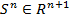кеңістігінің желімделген нүктелер жұбының 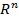де сәйкес қарама-қарсы нүктелерді центр еткен 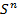-дегі ашық шарлар маңайлар жұбына гомеоморфты маңайы бар.

4-мысал. 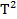-тор өлшемді көпбейне (58-сурет).

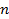-өлшемді көпбейненің анықтамасынан оның әрбір нүктесінің сызықты байланысты маңайға ие болатындығын көреміз. Сондықтан 3-теоремаға сәйкес көпбейненің байланыстылығы шығады. 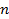-өлшемді көпбейненің әрбір байланысты компонентінің өзі де 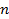-өлшемді көпбейне бола алады. Төменде байланысты көпбейнелер ғана қарастырылады. 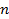-өлшемді көпбейнеге тек жалғыз нүктелі жиындар ғана жатады.

Компактылы көпбейнені көбінесе тұйық көпбейне, ал компактылы емес көпбейнелерді – ашық көпбейне деп атайды. Бұл тараудың мақсаты бір өлшемді және екі өлшемді көпбейнелерді топологиялы классификациялау (дәлелдеусіз). Бір өлшемді байланысты көпбейнелерді классификациялау қиын емес. Ол келесі теоремада берілген.

Теорема 2. Кез келген бір өлшемді компактылы (тұйық) топологиялық көпбейне 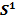-шеңберге геоморфты. Кез келген бір өлшемді компактылы емес (ашық) топологиялық көпбейне 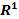-ге гомеоморфты.

Екі өлшемді компактылы көпбейнелерді классификациялау қиынырақ. Ол үшін кейбір жаңа ұғымдарды енгізу қажет болады.

Жиекті көпбейне

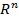кеңістіктің 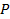гипержазықтықпен шектелген жарты кеңістігін 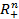деп белгілелік.

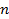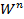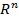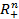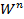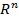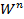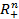-өлшемді жиегі бар көпбейне деп саналымды базасы бар, әрбір нүктесінің -ге немесе -ге гомеоморфты маңайы бар болатын хаусдорфты топологиялық кеңістікті айтамыз. Жиегі бар көпбейненің -ге гомеоморфты маңайы бар нүктелерін ішкі нүктелер деп, ал -нің -ге гомеоморфты маңайы бар нүктелерін жиек нүктелері дейміз. Ішкі нүктелерді 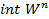деп белгілеу қабылданған. 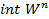жиыны да 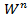кеңістігінде ашық жиын және ол да 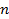-өлшемді топологиялық көпбейне. Сондықтан 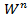-де оның жиек нүктелер жиыны тұйық; оны 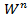-нің жиегі деп атап ∂ 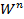-деп белгілейді. 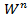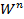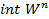көпбейнесінде ∂ жиыны жиынына шекара, сондай-ақ, 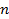-өлшемді топологиялық көпбейне жиегі бар көпбейненің дербес жағдайы. Оның жиегі бос жиын болады. Келесі теорема орынды.

Теорема. Егер 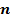-өлшемді жиегі бар 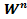көпбейненің жиегі ∂ 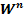бос жиын болмаса, онда ол 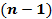өлшемді көпбейне болады. Егер 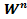компактылы болса, онда оның жиегі де компактылы (тұйық) көпбейне.

Жоғарыдағы айтылғандарды елестетуге көмектесетіндей мысалдарды келтірейік.

1-мысал. Тұйық 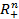жарты кеңістік 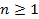болғанда жиегі бар көпбейне болады. Оның жиегі ∂ 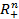= 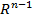. Егер де 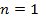болса, онда 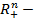сәуле, ∂ 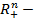нүкте. Егер де 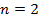болса, онда 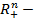жарты жазықтық, ал ∂ 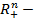түзу.

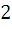-мысал. 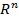-дегі 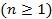тұйық 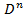шар – жиегі бар көпбейне болады. Оның жиегі -∂ 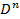сфера - 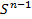болады.

Егер 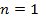болса, онда 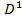– кесінді, ал 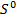- екі нүктеден, кесіндінің ұштарынан тұрады. Егер 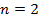болса, онда 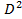– дөңгелек, ∂ 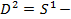оны шектеуші шеңбер.

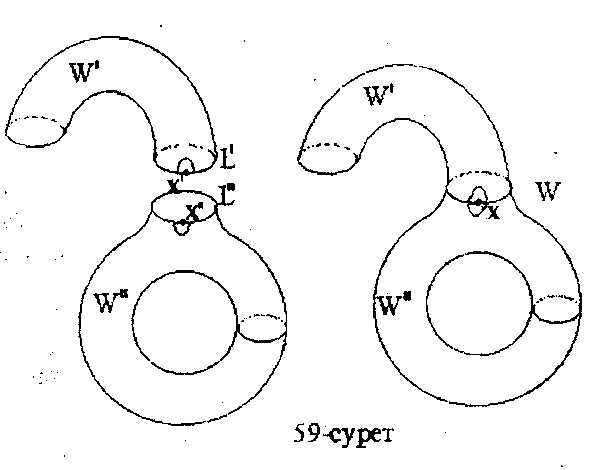
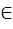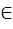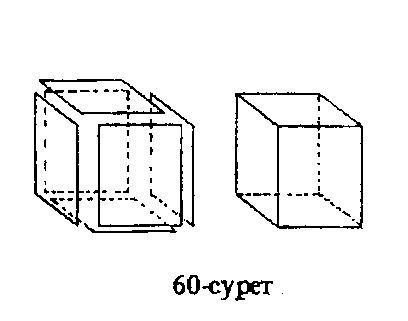
Екі өлшемді көпбейнелерді классификациялау үшін қажетті кейбір мысалдар «желәмдеу» амалының көмегі арқылы алынады. Оның мәні мынадай. Жиегі бар екі W' және W" көпбейне алып, олардың ∂W', ∂W" жиектерінде қайсыбір гомеоморфты L', L" бөліктер алынады (59-сурет). X' L' және X" L" сәйкес нүктелері бір Х нүктеде желімделеді. X' және X" нүктелерінің желімделген маңайлары Х нүктесінің маңайы деп есептеледі. W' және W" көпбейнелерін желімдеу (қандай да бір 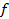гомеоморфизмге сәйкес) арқылы жаңа жиегі бар W көпбейне аламыз. Мысалы, көпжақты бетті, оны жақтарын желімдеу арқылы алынған деп түсінуге болады (60-сурет). Ал айналу цилиндірінің бетін – оның бүйір беті мен екі табанының желімдеуінен алынған деуге болады (61-сурет).

3-мысал. 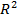жазықтықта 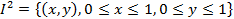квадратын қарастыралық. Квадраттың (0,y) және (1,y) нүктелерін «теңдестірелік», яғни оның қарама-қарсы екі қабырңасын желімделік (62-сурет). Сонда цилиндрдің бүйір бетіне гомеоморфты болатын екі өлшемді жиегі бар 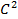көпбейне аламыз. Оның ∂ 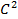жиегі екі 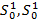шеіберден тұрады.

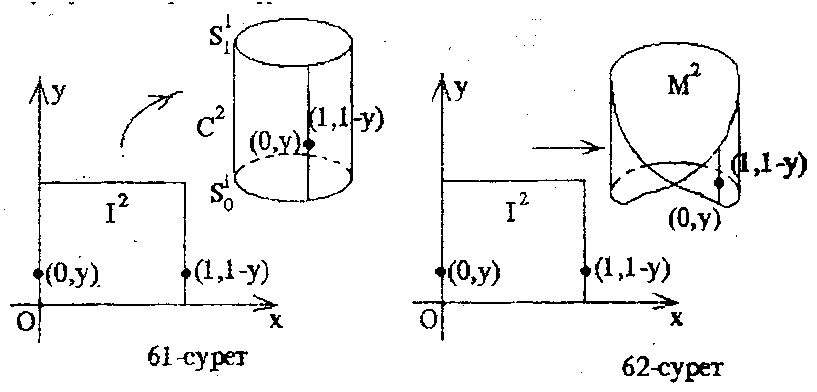
4-мысал. Алдыңғы мысалдағы 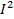квадраттың (0,y) және (1,1-y) нүктелерін теңестірелік. 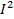квадраттың нүктелерін осы әдіспен желімдеуден алынған 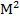көпбейнені «Мëбиус жапырағы» деп атайды. Мëбиус жапырағын алу үшін квадраттың қарама-қарсы қабырғаларын желімдемес бұрын оларды айналдыра бір рет бұраймыз (62-сурет).

Жиегі бар көпбейне бола алатын 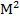- Мëбиус жапырағының жиегі -∂ 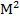шеңберге гомеоморфты, сондықтан Мëбиус жапырағы цилиндрлік бетке гомеоморфты болмайды.

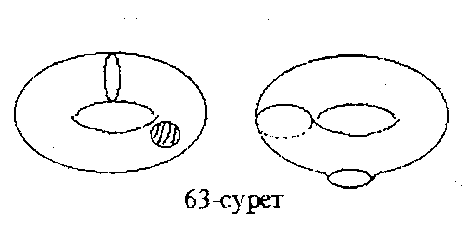
5-мысал. Егер 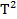- тордан ашық дөңгелекке гомеоморфты жиынды шығарып («кесіп») тастасақ, онда тордың қалдығы, жиегі 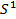шеңбер болатын, жиекті көпбейне 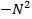болады. Оны «тұтқа» деп атайды (63-сурет).

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:

№ 12 дәріс Беттiң Эйлерлiк сипаттамасы. Беттерді топологиялық жiктеу ұғымы. Көпжактар үшiн Эйлер теоремасы (1с)

Жоспары

1. Беттiң Эйлерлiк сипаттамасы.

2. Беттерді топологиялық жiктеу ұғымы. Көпжактар үшiн Эйлер теоремасы

Беттің сызықтық элементі

Ф элементарлық беті, uv – жазықтығының G облысын топологиялық түрлендіруден алынған болсын. G облысыныда 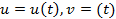қисығын алалық. G облысын Ф бетіне көшіретін түрлендіру , бұл қисықты Ф бетінің 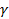қисығына көшіреді Ф беті 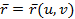- векторлық теңдеуімен берілсе, онда 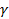қисығы 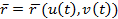теңдеуімен беріледі.

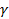қисығының ұзындығы

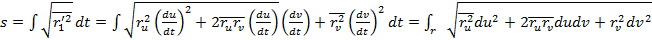(1)

мұндағы ∫_r интегралдау 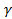қисығының бойымен алынады дегенді білдіреді.

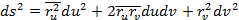
Квадраттық форманы, беттің бірінші квадраттық формасы немесе сызықтық элементі деп атайды. Бұл квадраттық форманың коэфициенттері үшін біз

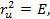
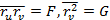
белгілеулерін пайдаланымыз.

(1) формуладан, беттегі қисықтың ұзындығын табу үшін, беттің бірінші квадраттық формасын білу жеткілікті екенін көреміз. Осыған байланысты бірінші квадраттық форма беттің метрикасын береді деп атайды.

G облысында, (u₀,v₀) нүктесінде қиылысатын, 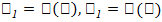және

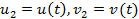екі қисық берілсін. Оларға Ф бетінің үстінд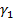е және 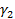қисықтары сәйкес болады. Ортақ Р(u₀,v₀) нүктесінде осы 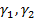қисықтарының арасындағы бұрыш деп, олардың жартылай жанамаларының арасындағы бұрышын айтады (34-сурет). Сонымен

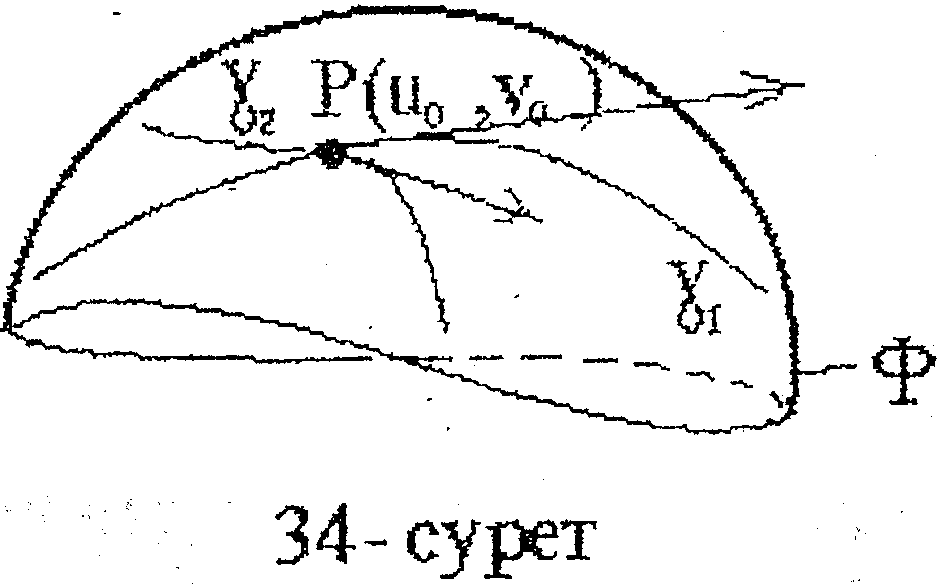
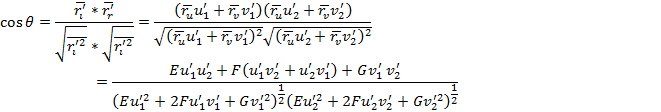
Егер 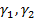қисықтарының бойымен u және v арқылы дифференцилдауды, d және δ деп белугілеуге келіссек, онда жоғарыдағы формуланы

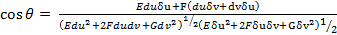(2)

(2) формуладан да беттегі екі қисықтың арасындағы бұрыш бірінші квадраттық формамен анықталатынын көреміз.

Енді қандай шарт орындалғанда беттің координаталық торы u, v ортогональдық болатынын, яғни тікбұрыш жасап қиылысатынын анықталық. U сызығының бойымен du 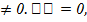ал сызығының бойымен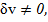

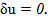
Сондықтан u, v торы ортогонольдық болады, 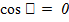, сонда тек қана сонда, егер F 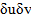=0, яғни F=0 болғанда.

Изометриялы беттер. Беттерді майыстыру

Егер S₁ және S₂ регулярлық беттердің нүктелерінің арасында, сәйкес қисықтардың ұзындықтары бірдей болатындай өзара бір мәнді сәйкестік орнатуға болса, онда бұл беттерді изометриялы деп атайды. Изометриялы беттердің бірінші квадраттық формалары бірдей болатындай параметризациялауға болады. Изометриялы беттер түсінігімен тығыз байланысты тағы бір түсінік беттерді майыстыру.

Егер S₁ ,S₂ екі регулярлық беттің арасында изометриялық қатынас орнатылса, онда S₂ беті S₁ бетін майыстыру арқылы алынған деп атайды.

Майыстырудың мысалын келтірейік. Бізге АВСД тік төртбұрышты парақ берілсін.

Бір парақтың АВ және СД қабырғаларында жатқан тұтас нүктелерді бір нүкте деп есептелік. Яғни В мен С,А мен Д,N мен (35-сурет) бір нүктелер болсын. Онда сол парақтың 35-суреттің оң жағындағы цилиндрді

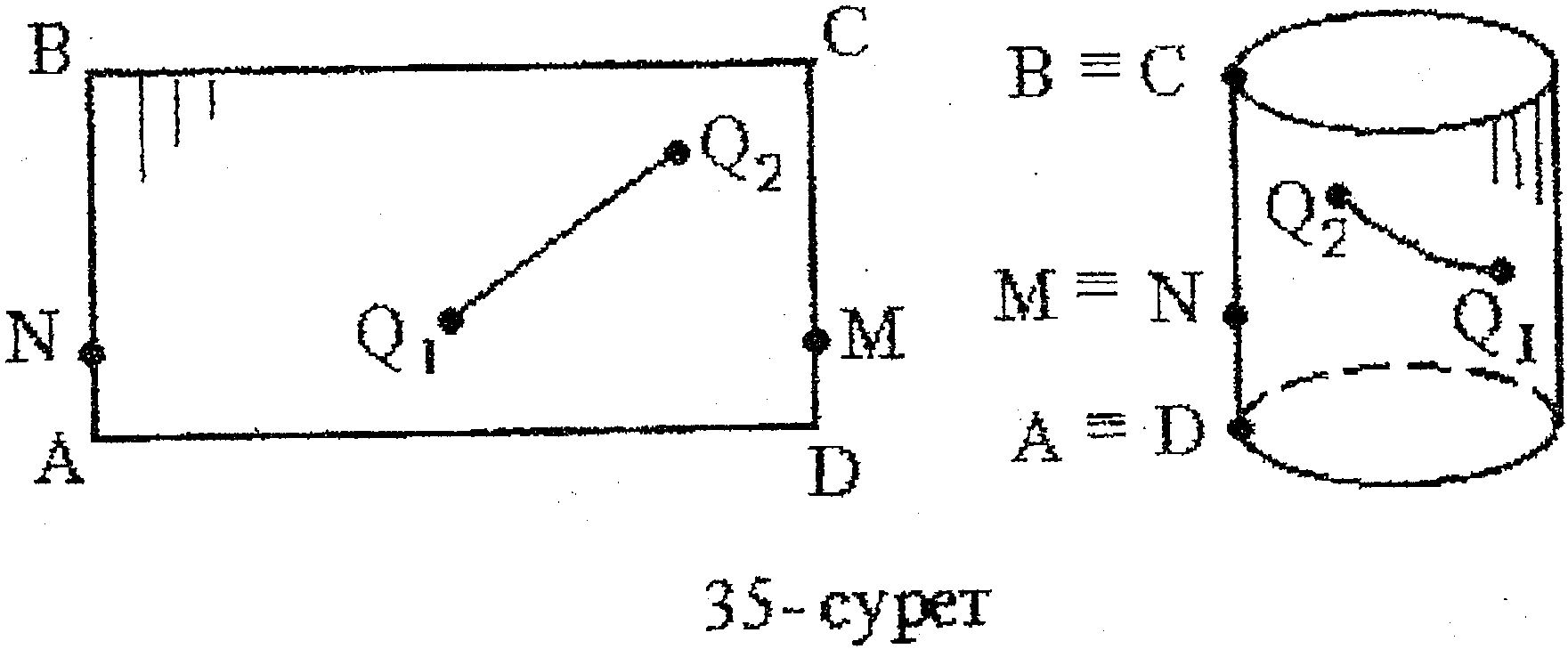
майыстырумен алдық деуге болады. Шынында да, олардың нүктелерінің арасында бір мәнді сәйкестік орнатуға болады. Әрбір нүктеге майыстырудан кейінгі шыққан беттің сол гүктесін сәйкестікке қоямыз. Осы екі беттің изометриялық беттер болатыны түсінікті.

Беттерді аз маңайында майыстыруға болады, ал «бүкіл» бетті майыстыруға әр уақытта болады деуге болмайды. Мысалы, сфераны майыстыру мүмкін емес.

Бетті түрлендіру қисықтардың арасындағы бұрыштарды сақтаса, онда ол конформды түрлендіру деп аталады. Конформды түрлендіру карта жасау ісінде үлкен рөл атқарады. Географиялық карталар жер бетіндегі облыстардың конформды кескіндерін береді.

Беттің ауданы

Тегіс Ф-беті берілсін. Оны ұсақ g облыстарға бөлшектелік. Осы облыстардың әрқайсысында Р нүктесін алалық және бұл облысты осы Р нүктедегі жанама жазықтыққа проекциялалық. Осы проекцияның ауданын s(g) делік. Бөлшектенген g облысының өлшемі кемігенде 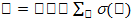шамасын Ф бетінің ауданы деп атайды.

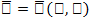теңдеуімен берілген беттің ауданы үшін формуланы табалық.

Ең бірінші s(g)- ны өрнектелік. Р нүктесін координаталар басы етіп, ал осы нүктедегі жанама жазықтықты хОу-деп х,у,z декарт координаталарын енгізелік. Осы координаталарда g облысындағы бет

x=x(u,v), y=y(u,v), z=z(u,v)

теңдеулерімен берілсін.

g облысының өлшемі мейлінше аз болғанда оны жанама жазықтыққа (хОу жазықтығына) бір мәнді проекциялауға болады. Сондықтан, проекциядағы қисық сызықты координаталар деп u,v-ны алуға болады. Анализден, жазық облыстың ауданы қисық сызықты координаталарда

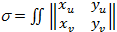dudv

Формуласымен анықталатыны белгілі.

Интеграл астындағы өрнекті

=

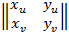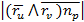
түрінде жазамыз, мұндағы 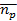Р нүктесінде бетке бірлік нормаль вектор.

Бұдан кейін

,

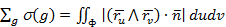мұндағы 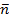, әрбір g облыста тұрақты, осы облыстың Р нүктесіндегі бірлік нормаль векторға тең, беттегі вектор-функция. g облысының өлшемі шексіз кемігенде шекке көшіп, беттің ауданын есептеу формуласын аламыз:

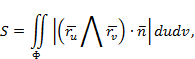
немесе

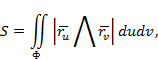
себебі 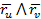векторлары өзара коллинеар.

-

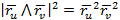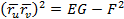
екенін ескерсек,

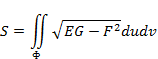
аламыз. Бұл формуладан, біз беттің ауданы да бірінші квадраттық формамен анықталатынын көреміз.

Бет z=z(x,y) түріндегі берілсе, онда

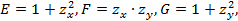
сондықтан

S=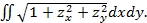

№ 13 дәріс Евклидтік кеңістіктегі сызықтар. (1с)

Жоспары

1. Сызык ұғымы.

2. Жазық қисыктар.

3. Жанама.

4. Қисықтың ұзындыгы.

5. Иiлiм және бұралым.

Евклидтік кеңістіктегі сызықтар.

1. V кеңістігі үш өлшемді векторлық евклидтік кеңістік және (а,b) аралығы бір сандық интервал болсын. Сонда

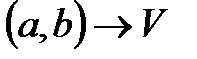
бейнелеуі әрбір 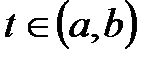санына V кеңістігінің белгілі бір векторын сәйкестендіреді. Бізге бұл векторды 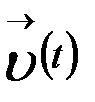арқылы белгілеу қолайлы болады. Сөйтіп, біз t скаляр аргументтің 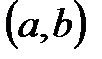интервалында анықталған 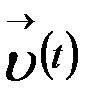векторлық функциясына келеміз.

Егер 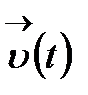векторының 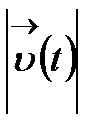нормасы 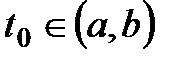нүктесінің маңында шектеусіз аз функция болса, онда 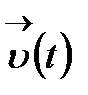векторын сол нүктенің маңында шектеусіз аз вектор дейді. 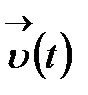векторының 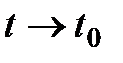болғандағы шегі деп, 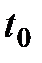нүктесінің маңында 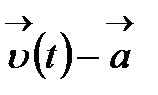айырмасы шектеусіз аз болатындай, тұрақты 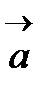векторын айтады. Мұны былай жазады: .

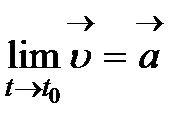Егер әрбір 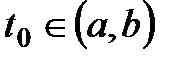нүктесінде

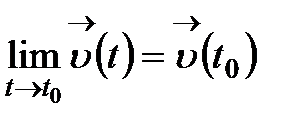
теңдігі орындалатын болса, онда 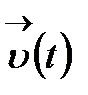векторлық функциясын (а,b) интервалында үздіксіз функция дейді.

Бір 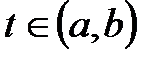нүктесін алып, t аргументке 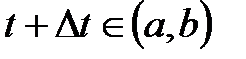болатындай етіп, 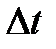өсімше берейік. Содан кейін 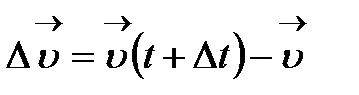векторын табайық.

Егер 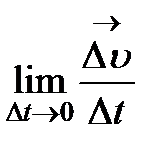шегі бар болса, онда 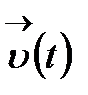функциясы t нүктесінде дифференциалданатын функция деп аталады, біз бұл шекті 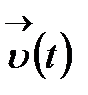немесе 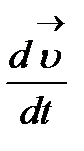арқылы белгілейміз. Айтылып отырған шек 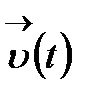функциясының 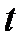нктесіндегі туындысы деп аталады, ал 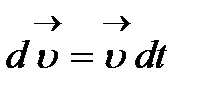векторы 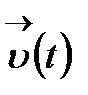функциясының дифференциалы деп аталады.

V векторлық кеңістіктің ортонормаль базисі 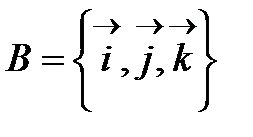болсын. 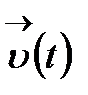векторын В базисінің векторлары бойынша жіктеп жазайық:

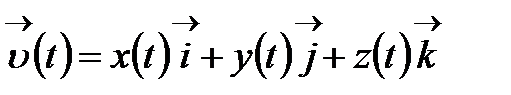
Енді мына векторды қарастырайық:

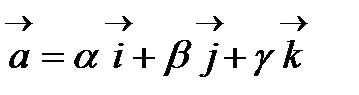
Мынаны табамыз:

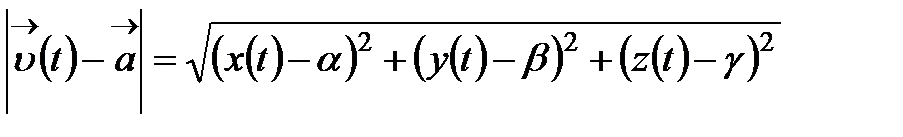
Бұдан шығатыны:

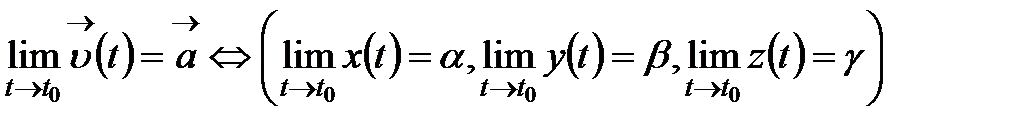
Одан әрі табатынымыз:

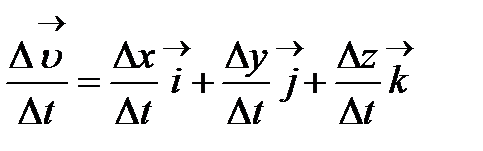(1)

мұнда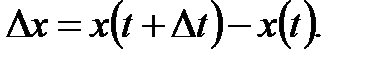

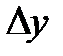пен 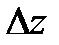өсімшелерінің мағыналары да осы сияқты болады.

(1) теңдіктен, тек 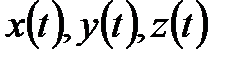функцияларының әрқайсысы дифференциалданғанда ғана 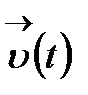функциясы дифференциалданады деп қорытамыз. Бұл жағдайда мына теңдік дұрыс болады:

.

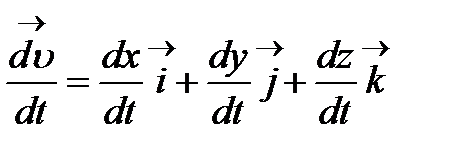Сонымен, 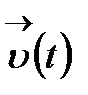векторлық функцияны дифференциалдау оның 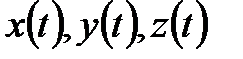координаталарын дифференциалдауға келтіріледі.

2. Скаляр аргументтің векторлық функцияларына сәйкес дифференциалдау ережелері әдеттегідей орындалады:

1) ;

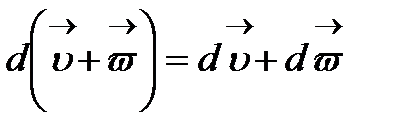2) ;

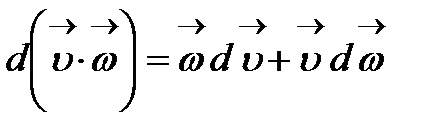3) ;

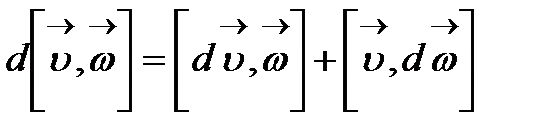4) .

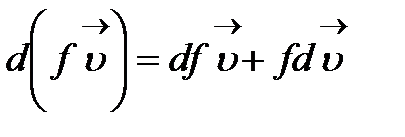Сызық ұғымы. 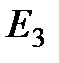кеңістігіндегі теріс қисықтар

1.R сандық түзудегі бір өлшемді көпбейнеліктер (немесе шеті бар бір өлшемді көпбейнеліктер) 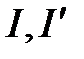және белгілі бір n өлшемді 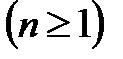көпбейнелік 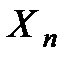болсын. 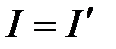жағдайы да санатқа қосылады. Егер 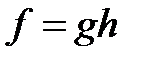орындалатындай 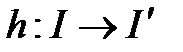гомеоморфизм бар болса, онда

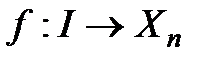және

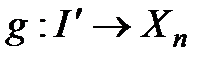
матырулар 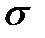қатынаста болады дейміз. Соңғысы мынаны білдіреді:

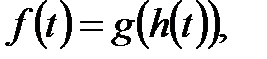
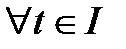. (2)

Rтүзуіндегі бір өлшемді көпбейнеліктерді 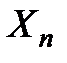көпбейнелікке матырулардың L жиынында 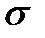эквиваленттік қатынасы болатынын тексеруді оқырмандарға ұсынамыз. 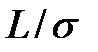факторжиынының әрбір элементі 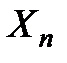көпбейнелікті сызық (немесе қисық) деп аталады.

Сөйтіп, Х көпбейнеліктегі қисық дегеніміз 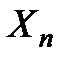көпбейнеліктегі бір өлшемді көпбейнеліктердің эквивалент матырулардың класы болады. Әрбір 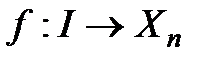матыру өзіне эквивалент матырулардың класын бір мәнді анықтайды. Сондай-ақ, f матыруды 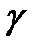қисықты параметрлеу деп те атайды.

Егер 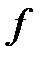және 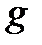матырулар эквивалент болса, онда (2) теңдік көрсеткендей,

,

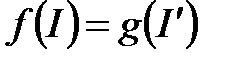Яғни эквивалент матырулар 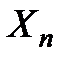көпбейнелігінде бірдей бөлімше жиынды өзінің бейнесі етіп алады.

Егер 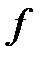матыру енгізу болса, онда оның 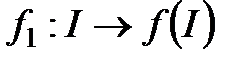келтіруі гомеоморфизм болып табылады. Демек, 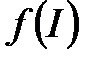бөлімше кеңістіктің өзі 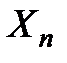көпбейнелікте көпбейнелік болып табылады; бұл 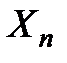көпбейнеліктің бір өлшемді бөлімше көпбейнелігі деп аталады. Әдетте, 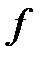енгізуімен анықталатын 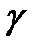қисықты 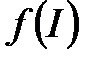жиынымен теңбе-тең түрде қарастырады.

2. Қисықтардың дербес жағдайларын атап өтейік:

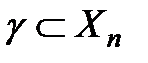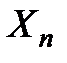1) Егер қисық ішіндегі белгілі бір 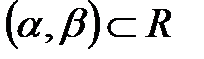, интервалды енгізумен анықталса, онда ол қисық элементар қисық деп аталады. Түзу сызық, синусоида - 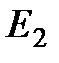жазықтығындағы элементар қисықтардың мысалдары.

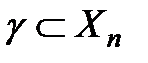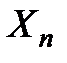2) Егер қисық ішіндегі бөлімше көпбейнелік болса, онда ол сызық жай қисық деп аталады. Кез келген элементар қисық жай қисық болып табылады. Шеңбер 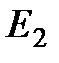жазықтығындағы жай қисықтың мысалы, ол элементар қисық бола алмайды.

3) 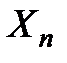ішіндегі 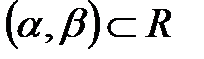кесіндісінің 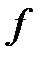матыруы шеткі нүктелері 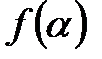және 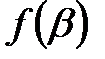болатын сызықты анықтайды, ол доға деп аталады.

3. 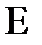3 евклидтік кеңістікте ортонормаль 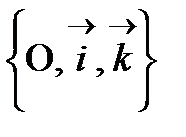реперді берейік және 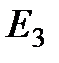кеңістігіндегі 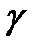қисықты қарастырайық, бұл 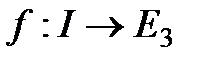матырумен анықталады.

Егер 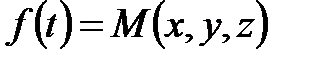болса, онда

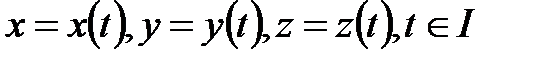(3)

Демек, 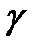қисығын сызатын М нүктесінің 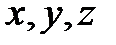координаталары 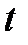параметрінің 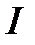аралығында анықталған функциялары болып табылады. (3) теңдіктер 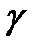қисығының 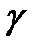қисығының параметрлік теңдеулері деп аталады.

Матырудың анықтаиасынан (3) теңдеулердің оң жақтары – І аралығындағы үзіліссіз функциялар екені шығады. Алайда, егер (3) түріндегі теңдеулерді алдымен жазса, оның оң жақтары – үзіліссіз функциялар, онда бұл теңдеулер І аралығының матыруын бермеуі де мүмкін, яғни ешқандай қисықты анықтамайды. Мәселен, 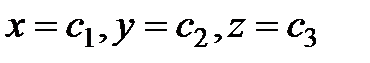теңдеулері, мұның оң жақтары тұрақты, сызықты емес, нүктені анықтайды.

Егер 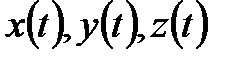функциялары 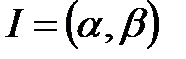интервалда үзіліссіз және осы функциялардың ең болмағанда біреуі осы интервалда қатаң бірсарынды болса, онда (3) теңдеудің элементар қисықты анықтайтынын дәлелдеуге болады.

4. Егер 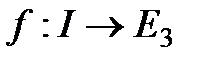матыруды беретін (3) теңдеулердің оң жақтары І аралығында қоса есептегенде к ретке дейін үзіліссіз туындылары бар, оның үстіне 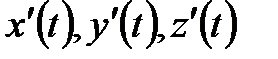бірінші ретті туындылары І аралығының нүктесінде бәрі бірдей нольге айналмайтын функциялар болса, онда 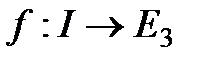матыру 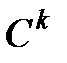-матыру (немесе 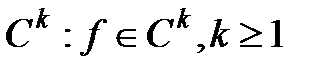класқа тән) деп аталады.

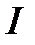және 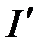екі аралық болсын. Егер 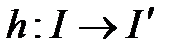бейнелеу биективті және 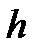пен 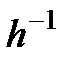бейнелеулердің екеуі де (әрқайсысы өзінің аралығында) қосып есептегенде 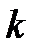ретке дейін үзіліссіз туындылары бар болса, онда 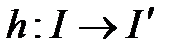бейнелеуі 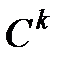-диффеоморфизм деп аталады.

Мұндай бейнелеу гомеоморфизмнің дербес жағдайы екені даусыз.

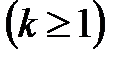
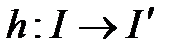
Егер 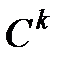-диффеоморфизм 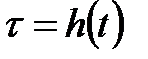теңдеуімен берілсе, онда 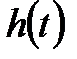функциясының 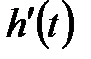туындысы І аралығының ешбір нүктесінде нольге айналмайтынын және осы аралықта таңбасын сақтайтынын байқау қиын емес.

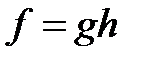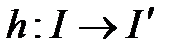
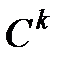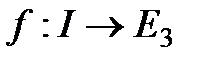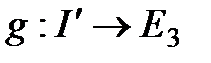Егер болатындай -диффеоморфизм бар болса, онда біз және -матырулар 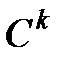-эквивалентті деп айтамыз.

5. Кеңістікте түзу сызықты түзудің 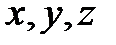нүктесінің координаталарына сәйкес тәуелсіз екі сызықтың теңдеуінің системасымен беруге болады. Әрине мынадай жалпы сұрақ туады: қандай жағдайда теңдеулердің

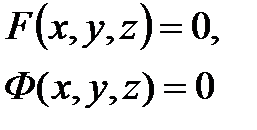(4)

системасы тегіс қисықты анықтайды?

Бұл сұраққа жауапты анализден белгілі жабық функциялар жайындағы теоремадан аламыз. Атап айтқанда, координаталары (4) системаның теңдеулерін қанағаттандыратын кеңістіктің нүктелерінің жиыны 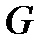болсын. 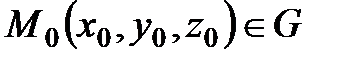нүктесі, мына екі шарт орындалатындай нүкте болсын:

1) 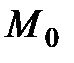нүктесінің белгілі бір 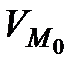аймағында (4) теңдеулердің сол жақтары үзіліссіз және бірінші ретті үзіліссіз туындылары бар,

2) 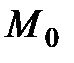нүктесінің өзінде

.

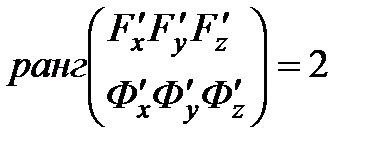Онда, 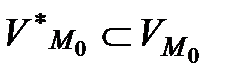қиылысуы 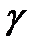тегіс қисық болатындай 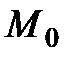нүктесінің 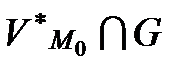аймағы бар.

Егер 2) шартта көрсетілген матрицаның соңғы екінші ретті миноры нольден өзгеше болса, онда 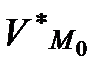аймағында (4) теңдеулер системасы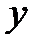н пен 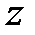-ке сәйкес шешуге болады. Біз мыналарды аламыз: 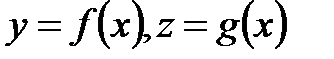. Анализден 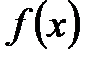және 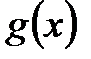функцияларының бірінші ретті үзіліссіз туындылары бар екені белгілі. Демек, теңдеулері 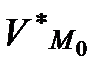аймағында 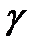тегіс қисықты анықтайды.

6. (3) үш теңдеу бір векторлық теңдеуге бара-бар:

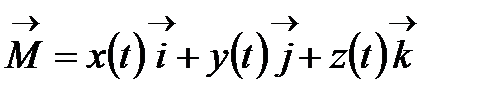, (5)

қысқаша, 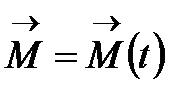, мұндағы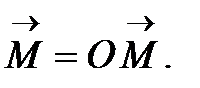

Сонымен, 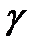сызықты сызатын М нүктесінің радиус векторы І аралықта анықталған 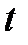скаляр аргументті 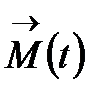вектор функциясы болады. 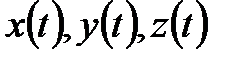функцияларының І аралығында қосып есептегенде 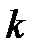ретке дейін үзіліссіз туындылары бар болғанда ғана (5) теңдеу 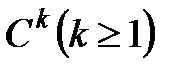класты тегіс қисықты анықтайды және .

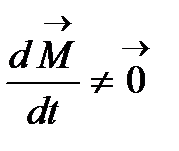$ 12. Жанама. Доғаның ұзындығы.

1. (5) теңдеумен берілген 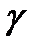тегіс қисықты қарастырайық. Осы қисықтан әр түрлі 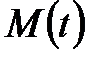және 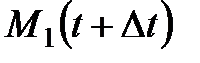екі нүктені алайық. Мына вектор

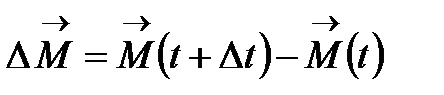
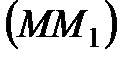түзуінің қиюшысының бағыттауыш векторы болып табылады. 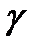қисығы тегіс болғандықтан, кез келген 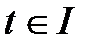нүктесінде мына туынды бар

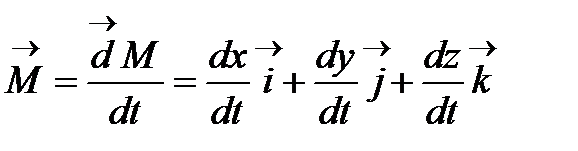
және бұл туынды нольден өзгеше.

Егер 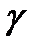қисықтың басқа 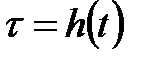параметрлеуін алсақ, онда:

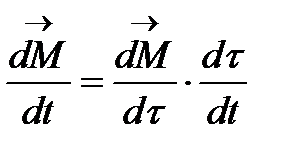
Демек, 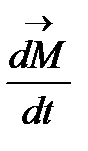және 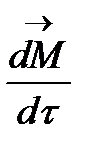векторлары коллинеар. Оның үстіне, 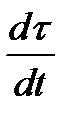туынды І аралығында таңбасын сақтағандықтан, 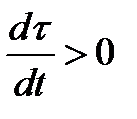болғанда әрбір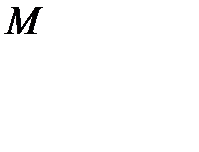

Дюпен индикатрисасы осьтерінің бағыттарын біз бас бағыттар деп атадық. Кейіннен бас бағыттар бойынша нормаль иілім өзінің экстремальдық мәндерін кабылдайтынын орнаттық. Демек, соңғы қасиетен біз бас бағыттарды анықгай аламыз деген сөз. Бұлай анықтағанда бас бағыт түсінігін, тіпті, Дюпен индикатрисасы болмайтын жайылым нүктесі үшін де анықтауға болады. Жайылым нүктесінде нормаль иілім кез-келген бағытта нөлге тең болғандықтан , кез-келген бағыт бас бағыт болады.

Жалпы жағдайда беттің кез-келген нүктесінде екі бас бағыт бар. Тек жайылу нүктесі мен Дюпен индикатрисасы шеңберге айналатын эллипстік нүктені (жұмыр нүкте) бөліп қарастырған жөн. Мұндай нүктелерде кез-келген бағыт бас бағыт бола алады.

Беттегі 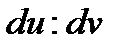бағыты бас бағыт болуы үшін қандай шарт орындалуы керек екен, соны тексерелік. Бізге

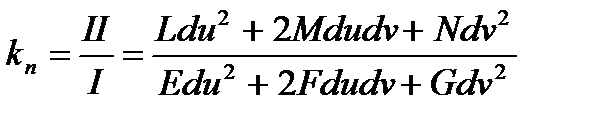
формуласы белгілі. Өрнектің оңжағы 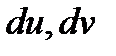айнымалыларының функциясы және бұл функция бас бағыттар үшін өзінің экстремаль мәндерін қабылдайтын болғандықтан, онын осы айнымалылар бойынша туындылары нөлге тең. Демек,

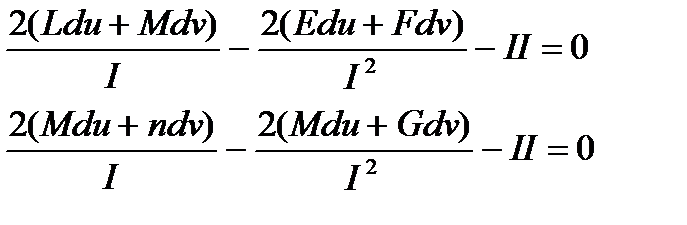
Бұл теңдеулерден

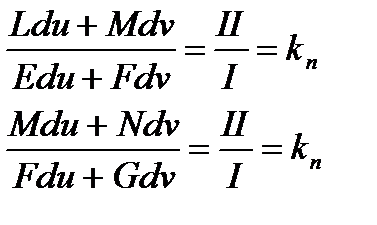
теңдіктер аламыз. Оларды теңестіріп,бас бағыттар үшін төмендегі теңдеуді аламыз:

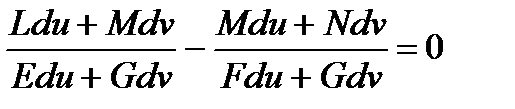
Бұл теңдеуді еске сақтауға ыңғайлы түрде жазалық.

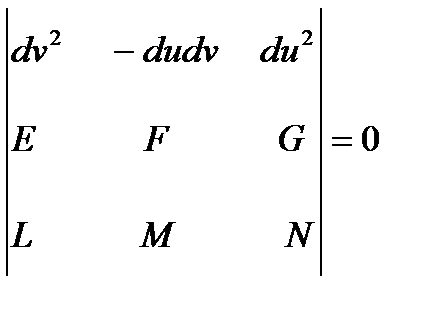
Егер беттегі сызықтың әрбір нүктесіндегі бағыт бас бағыт болса, онда сызық иілім ығы деп аталады. Бұдан иілім сызығының дифференциалдык теңдеуі (* ) түрінде болатындығы шығады.

Егер беттің жазылу және жұмыр нүктелері жоқ облысында координиталық тор иілім сызықтарынан тұрса, онда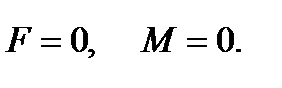

Шындығында, мұндай облыстың әрбір нүктесінде бас бағыт екеу. Олар ортогональ және түйіндес. Демек,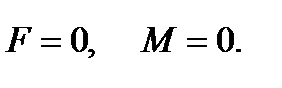

Родриг теоремасы.Беттегі бас бағыт бойынша дифференциалдық,

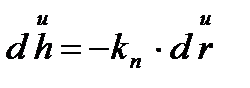
мұндағы k 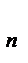- бағыттағы нормаль иілім.

Дәлелдеуі: u сызығының бағыты берілген нүктеде бас бағыт болатындай және осы нүктеде коррдинаттық сызықтар ортогональ болатындай етіп u,v координаталық торын енгізелік. 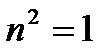, сондықтан, 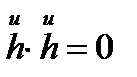, яғни 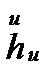векторы 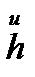-ге перпендикуляр, демек, оны 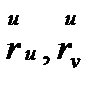векторлар бойынша жіктеуге болады:

.

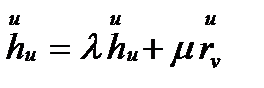бұл теңдіктің 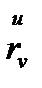- ге скаляр көбейтіп және 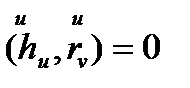(ортогональдығы), 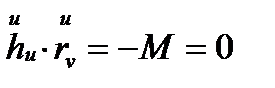(түйіндестігі) екенін ескеріп, 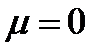аламыз. Енді 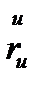-ға көбейтсек

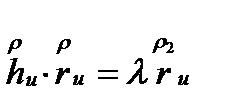
немесе 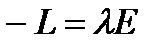. Бұдан беттің 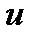бағытындағы нормаль иілімнің , 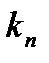яңғни аламыз. Сонымен

.
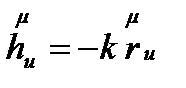