Структурная устойчивость

Пусть какая-либо система задана своей структурной схемой, то есть известно, из каких звеньев она состоит, и какого рода связи осуществляются между звеньями. Совокупность положительных числовых значений всех постоянных времени и иных коэффициентов, которые необходимо знать для получения коэффициентов характеристического уравнения, носит название параметров системы. Изменение отличных от нуля параметров системы не вызывает изменения ее структурной схемы.

В ряде случаев оказывается, что система неустойчива при любых значениях своих параметров, и добиться ее устойчивости можно только путем изменения структурной схемы. Такие системы называют структурно неустойчивыми, в отличие от структурно устойчивых систем, которые могут быть сделаны устойчивыми простым выбором соответствующих параметров.

Пример 14.Проверить на структурную устойчивость замкнутую систему (с единичной отрицательной обратной связью) в составе неустойчивого инерционного звена (рисунок 2.5).

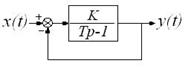
Рисунок 2.5 – Замкнутая система в составе неустойчивого

инерционного звена

Рассчитаем передаточную функцию системы:

,

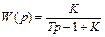откуда характеристическое уравнение примет вид

.

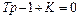Система имеет 1-й порядок, поэтому для ее устойчивости достаточно обеспечить строгую положительность коэффициентов характеристического уравнения:

,

.

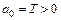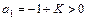Выполнение 1-го неравенства очевидно, поскольку постоянная времени 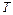может принимать только положительные значения. Для выполнения 2-го неравенства необходимо, чтобы значение коэффициента усиления было выбрано из условия .

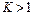Таким образом, найдено такое сочетание значений параметров системы 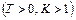, при котором достигается ее устойчивость. Это означает, что данная система структурно устойчива.

Пример 15.Проверить на структурную устойчивость замкнутую систему (с единичной отрицательной обратной связью) в составе интегрирующего и неустойчивого звеньев (рисунок 2.6).

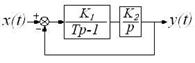
Рисунок 2.6 – Замкнутая система в составе неустойчивого

и интегрирующего звеньев

Рассчитаем передаточную функцию системы:

,

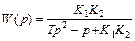откуда характеристическое уравнение, имеющее 2-й порядок, примет вид:

.

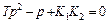Выпишем коэффициенты уравнения:

, , .

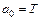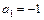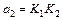Для устойчивости системы 2-го порядка достаточно обеспечить строгую положительность всех коэффициентов характеристического уравнения. Для коэффициентов 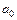, 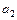это легко обеспечить за счет соответствующего выбора значений параметров системы

.

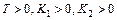На значение коэффициента 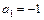изменение параметров системы влияние не окажет, поскольку он равен постоянной величине и от них не зависит.

Таким образом, условию устойчивости рассматриваемой системы удовлетворить невозможно ни при каких значениях параметров системы. Следовательно, данная система структурно неустойчива.

Пример 16. Проверить на структурную устойчивость замкнутую систему (с единичной отрицательной обратной связью) в составе интегрирующего, неустойчивого и форсирующего звеньев (рисунок 2.7).

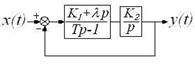
Рисунок 2.7 – Система с воздействием по производной

Рассчитаем передаточную функцию системы:

,

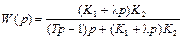откуда характеристическое уравнение, имеющее 2-й порядок, примет вид:

.

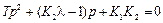Выпишем коэффициенты уравнения:

, , .

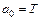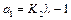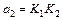Для устойчивости системы 2-го порядка достаточно обеспечить строгую положительность всех коэффициентов характеристического уравнения. Для коэффициентов 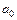, 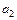это можно обеспечить за счет соответствующего выбора значений параметров системы

.

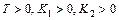Положительность коэффициента 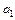возможна лишь при выполнении условия 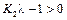, откуда следует, что параметр форсирующего звена 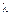должен быть выбран в виде .

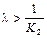Это означает, что подбором значений параметров звеньев можно добиться устойчивости рассматриваемой системы, поэтому она структурно устойчива.