Тема № 11 Анализ временных рядов

Задача 1

В таблице приводятся данные о потреблении и личных доходах населения за 1985-1991 гг.

Показатель	1985 г.	1986 г.	1987г.	1988 г.	1989 г.	1990 г.	1991 г.
Потребление, тыс. долл.
Личные доходы, тыс. долл.

Задание

Постройте уравнение линейной регрессии, используя метод первых разностей.

Охарактеризуйте тесноту связи между рядами по их уровням, по первым разностям. Сделайте выводы.

Задача 2

По данным за 30 лет изучается зависимость рентабельности продукции компании у{ (%) от численности занятых ручным трудом х( (чел.). Были получены следующие варианты уравнений регрессии:

а) по уровням временных рядов:

Ŷ_t = 2 - 0,5Χ_t + ε_t R² = 0,9025 d = 0,8;

б) по первым разностям уровней:

∆Ŷ_t =3 + 0,1 ∆Х_t+ε_t R² =0,49 d = 1,2;

в) по вторым разностям уровней:

∆²Ŷ_t = 15 - 0,062∆²Х_t + ε_t R² = 0,7225 d= 2,1;

г) по уровням рядов с включением фактора времени:

Ŷ_t= -7 - 0,02Χ_t+ 0,3t + ε_t R² = 0,95 d = 2,2.

t_ф= -(3,1) (3,7)

В таблице приведены известные коэффициенты автокорреляции первого порядка.

Ряд	По уровням ряда	По первым разностям уровней ряда	По вторым разностям уровней ряда
xt	0,99	0,80	0,05
yt	0,86	0,86	0,10

Задание

1. Определите коэффициенты корреляции по уровням временных рядов, по первым разностям временных рядов и по вторым разностям временных рядов. Охарактеризуйте тесноту связи между временными рядами рентабельности продукции и численности занятых ручным трудом. Обоснуйте ваш выбор одной из мер тесноты связи.

2. Исследуйте полученные уравнения регрессии на автокорреляцию в остатках.

Выберите наилучшее уравнение регрессии и дайте интерпретацию его параметров.

Форма проведения: Решение данных задач студентами самостоятельно на местах и при необходимости у доски.

Основная литература: [4, С.90-175], [10], [14]

Дополнительная литература: [20],[22],[23],[25], [32

Тема № 12 Система одновременных уравнений

Системы эконометрических уравнений.

Даны системы эконометрических уравнений.

Требуется:

1.Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.

2.Определите метод оценки параметров модели.

3.Запишите в общем виде приведенную форму модели.

Варианты индивидуальных заданий.

Вариант 1.

Модель протекционизма Сальватора (упрощенная версия):

где

– доля импорта в ВВП;

– общее число прошений об освобождении от таможенных пошлин;

– число удовлетворенных прошений об освобождении от таможенных пошлин;

– фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;

– реальный ВВП;

– реальный объем чистого экспорта;

– текущий период;

– предыдущий период.

Вариант 2.

Макроэкономическая модель (упрощенная версия модели Клейна):

где

– потребление;

– инвестиции;

– доход;

– налоги;

– запас капитала;

– текущий период;

– предыдущий период.

Вариант 3.

Макроэкономическая модель экономики США (одна из версий):

где

– потребление;

– ВВП;

– инвестиции;

– процентная ставка;

– денежная масса;

– государственные расходы;

– текущий период;

– предыдущий период.

Вариант 4.

Модель Кейнса (одна из версий):

где

– потребление;

– ВВП;

– валовые инвестиции;

– государственные расходы;

– текущий период;

– предыдущий период.

Планы занятий в рамках самостоятельной работы студентов

Тема №1Предмет и метод эконометрики

Написать рефераты на темы:

1. Роль эконометрии в подготовке экономистов в области экономики.

2. История эконометрики.

3. Нобелевские лауреаты в области эконометрики.

4. Эконометрика: сегодня и завтра.

5. Экономические и эконометрические модели.

6. Необходимость использования эконометрических методов в прикладных экономических исследованиях.

7. Методология эконометрики как науки.

Методические рекомендации: раскрыть сущность темы реферата 7-10 страницах формата А4.

Можно предложить свою тему реферата, имеющую практическую значимость.

Рекомендуемая литература: 1, 3, 4, 7, 8 ,10, 11, 12,15, 23, 27

Тема №3Основные статистические распределения

Задача 1

Процент протеина в пакете с сухим кормом для собак – нормально распределенная случайная величина с математическим ожиданием 11,2% и стандартным отклонением 0,6%. Производителям корма необходимо, чтобы в 99 % продаваемого корма доля протеина составляла не меньше х₁%, но не более х₂%. Найдите х₁ и х₂.

Задача 2

При производстве безалкогольных напитков специальный аппарат разливает определенное число унций (1 унция = 28,3 г) напитка в стандартную емкость. Число разлитых унций подчиняется нормальному закону с математическим ожиданием, зависящим от настройки аппарата Количество унций напитка, разлитых отдельным аппаратом, имеет стандартное отклонение = 0,4 унции. Пусть емкости объемом в 8 унций наполняются кока-колой. Сколько унций напитка должен в среднем разливать аппарат, чтобы не более 5 % емкостей оказалось переполненными.

Рекомендуемая литература : 6, 5, 11, 12 , 20, 32

Тема №4Статистические оценки распределения

Задача 1. Средняя продолжительность горения, установленная путем испытания 100 случайно отобранных электрических лампочек, оказалось равной 1280 ч. при среднем квадратическом отклонении 40ч. С какой вероятностью можно утверждать, что допущенная при этом предельная ошибка выборки не превысит 12ч.

Задача 2. Для определения средней заработной платы рабочих завода была произведена 20% -ная бесповторная выборка (по цехам) с отбором единиц пропорционально численности групп. Результаты выборки представлены в приводимой ниже таблице:

цех	объем выборки, человек	средняя заработная плата, тенге	среднее квадратическое отклонение, тенге
итого		х	х

С вероятностью 0,997 определить пределы, в которых находится средняя заработная плата всех рабочих.

Задача 3.В порядке случайной выборки обследован дневной надой молока 50 коров. Результаты обследования приведены в таблице:

Дневной надой, кг.	количество коров
10-14 14-18 18-22 свыше 22
Итого

Определить:

1) по выборочным данным средний надой молока от одной коровы;

2) среднюю ошибку выборки;

3) вероятность того, что при определении выборочного среднего надоя молока допущена ошибка, не превышающая 1 кг.

Задача 4. На предприятии проверен стаж работы у 12 мужчин и 8 женщин. Результаты наблюдения следующие:

группы рабочих	количество обследованных, человек	средний стаж работы, лет	среднее квадратическое отклонение стажа, лет
мужчины женщины

Рассчитать общий средний стаж работы для рабочих по выборочным данным; с вероятностью 0,954 определить доверительные пределы среднего стажа работы рабочих в генеральной совокупности.

Задача 5. Из партии готовой продукции в порядке механической бесповторной выборки проверено 400 изделий и установлено, что 80 % из них соответствует 1 сорту. С вероятностью 0,954 определить долю продукции 1 сорта во всей партии. Решать в 2-х вариантах: а) численность изделий в партии готовой продукции неизвестна; б) в партии готовой продукции 2000 изделий.

Задача 6. В банках города в порядке механической бесповторной выборки из 50 тыс. отобрали 5 тыс. счетов вкладчиков и по ним установили средний размер вклада 5000 тенге, при среднем квадратическом отклонении 180 тенге. Определите : а) предельную ошибку репрезентативности с вероятностью 0,997; б) вероятность того, что предельная ошибка выборки не превысит 4 тенге.

Рекомендуемая литература: : 6, 5, 11, 12, 20, 32.

Тема № 5Проверка гипотез

Задача 1. Компания, производящая средства для потери веса, утверждает, что прием таблеток в сочетании со специальной диетой позволяет сбросить в сред­нем в неделю 400 г. веса. Случайным образом ото­браны 25 человек, использующих эту терапию, и обнаружено, что в среднем еженедельная потеря в весе составила 430 г. со средним квадратическим отклонением 110 г. Проверьте гипотезу о том, что средняя потеря в весе составляет 400 г. Уровень значимости _.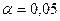

Задача 2. Поступление страховых взносов в 130 филиа­лов страховых организаций в регионе А составило 26*10⁴ у.е., в регионе В на 100 филиалов пришлось 18*10⁴ у.е. Дисперсия величины страховых взно­сов в регионе А равна 39*10⁸ (у. е.)², в регионе В – 25*10⁸ (у. е.)². На уровне значимости 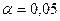опре­делите, существенно ли различается средняя ве­личина поступления страховых взносов в регионах А и В из расчета на 1 филиал.

Задача 3. Компания утверждает, что новый вид зубной пасты для детей лучше предохраняет зубы от кари­еса, чем зубные пасты, производимые другими фир­мами. Для проверки эффекта в случайном порядке была отобрана группа из 400 детей, которые пользо­вались новым видом зубной пасты. Другая группа из 300 детей, также случайно выбранных, в это же время пользовалась другими видами зубной пасты. После окончания эксперимента было выяснено, что у 30 детей, использующих новую пасту, и 25 детей из контрольной группы появились новые признаки кариеса. Имеются ли у компании достаточные ос­нования для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты? Принять уровень значимости .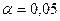

Задача.4. В 1995 г. число договоров добровольного стра­хования, заключенных государственными страхо­выми организациями, составило в Ростовской об­ласти 1858*10³ на сумму 7461*10⁶ д.е. Негосудар­ственные страховые организации заключили 1250*10⁴ договоров добровольного страхования на сумму 34884*10⁶ д.е. Предположительно дисперсия страховой суммы договоров, заключенных государственными страховыми организациями, равна 10¹⁶ д.е.², а договоров, заключенных негосударственными страховыми организациями, - 8*10¹⁷ д.е.². Имеются ли существенные различия в средних раз­мерах страховых сумм договоров добровольного страхования, заключаемых государственными и не­государственными страховыми организациями? Уровень значимости принять равным 0,01.

Задача 5. Крупный коммерческий банк заказал марке­тинговое исследование по выявлению эффекта «пре­мирования» (калькулятор, набор ручек и др.) как стимула для открытия счета в банке. Для проверки случайным образом было отобрано 200 «премиро­ванных» посетителей и 200 «непремированных». В результате выяснилось, что 89% посетителей, ко­торым предлагалась премия, и 79% посетителей, которым не предлагалась премия, открыли счет в банке в течение 6 мес. Используя эти данные, про­верьте гипотезу о том, что доля «премированных» посетителей, открывших счет в банке, статистичес­ки существенно отличается от удельного веса «не­премированных» посетителей, открывших счет в банке. Принять уровень значимости .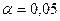

Задача 6. Инженер по контролю качества проверяет сред­нее время горения нового вида электроламп. Для проверки в порядке случайной выборки было ото­брано 100 ламп, среднее время горения которых со­ставило 1075 ч. Предположим, что среднее квадратическое отклонение времени горения для генераль­ной совокупности известно и составляет 100 ч. Ис­пользуя уровень значимости 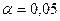, проверьте ги­потезу о том, что среднее время горения ламп - более 1 000 ч.

Предположим, что инженер по контролю каче­ства не имеет информации о генеральной диспер­сии и использует выборочное среднее квадратическое отклонение. Изменится ли ответ задачи?

Задача 7. Компания, выпускающая в продажу новый сорт растворимого кофе, провела проверку вкусов поку­пателей по случайной выборке из 400 человек и вы­яснила, что 220 из них предпочли новый сорт всем остальным. Проверьте на уровне значимости 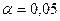гипотезу о том, что, по крайней мере, 52% потреби­телей предпочтут новый сорт кофе.

Задача .8. Страховая компания изучает вероятность до­рожных происшествий для подростков, имеющих мотоциклы. За прошедший год проведена случай­ная выборка 2 000 страховых полисов подростков-мотоциклистов и выявлено, что 15 из них попада­ли в дорожные происшествия и предъявили компа­нии требование о компенсации за ущерб. Может ли аналитик компании отклонить гипотезу о том, что менее 1% всех подростков-мотоциклистов, имею­щих страховые полисы, попадали в дорожные про­исшествия в прошлом году? Принять уровень зна­чимости .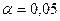

Задача.9. Новое лекарство, изобретенное для лечения атеросклероза, должно пройти экспериментальную, проверку для выяснения возможных побочных эффектов. В ходе эксперимента лекарство принимали 4 тыс. мужчин и 5 тыс. женщин. Результаты выявили, что 60 мужчин и 100 женщин испытывали побочные эффекты при приеме нового медикамен­та. Можем ли мы на основании эксперимента ут­верждать, что побочные эффекты нового лекарства у женщин проявляются в большей степени, чем у мужчин? Принять уровень значимости .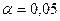

Задача 10. В 1995 г. в Ростовской области обследовано 12 промышленных предприятий и 14 строительных (подрядных) организаций. Средняя балансовая при­быль промышленных предприятий оказалась равной 25*10⁷pyб., а строительных организаций – 12*10⁸ д.е. Исправленная выборочная дисперсия прибыли про­мышленных предприятий составила 64*10¹⁶ д.е.², строительных организаций – 16*10¹⁶ д.е.². На уров­не значимости 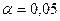определите, являются ли различия в результатах финансовой деятельности промышленных предприятий и строительных орга­низаций случайными.

Рекомендуемая литератур:1,3,4,5,7,8,10,11,12,115,17,24