Вопрос 27.2. Фундаментальная система решений (ФСР)

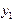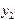Определение 27.1. Два любых решения и линейного однородного дифференциального уравнения образуют фундаментальную систему решений, если они линейно независимы.

ТЕОРЕМА 1. Если коэффициенты линейного однородного дифференциального уравнения непрерывны на некотором заданном промежутке, то оно имеет хотя бы одну Ф.С.Р. на этом промежутке.

ДОКАЗАТЕЛЬСТВО. Рассмотрим уравнение

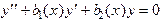
Зададим два начальных условия

.

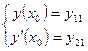
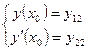Задача Коши всегда имеет только одно решение. Обозначим решение задачи Коши с первой группой начальных условий через 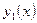, а со второй через 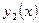. Начальные условия можно выбрать так, чтобы

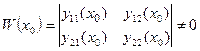
Тогда согласно следствию 3 решения 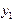и 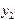линейно независимы и, следовательно, образуют Ф.С.Р.

КОНЕЦ ДОКАЗАТЕЛЬСТВА.

ЗАМЕЧАНИЕ 1. Из доказательства теоремы следует, что каждое линейное однородное дифференциальное уравнение имеет бесчисленное множество Ф.С.Р. (Это следует из возможности выбора начальных условий бесконечным числом способов).

ТЕОРЕМА 2. (Основная). Всякое решение линейного однородного дифференциального уравнения

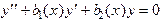
есть линейная комбинация решений из некоторой Ф.С.Р.

ДОКАЗАТЕЛЬСТВО. Согласно теореме 1 у уравнения имеется хотя бы одна Ф.С.Р. Пусть это решения 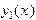и 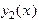и пусть y(x) есть произвольное решение уравнения. Составим систему уравнений

.

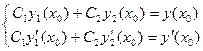Так как главный определитель системы уравнений есть определитель Вронского 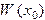и решения 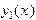и 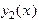образуют Ф.С.Р., то 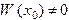. Поэтому эта система уравнений всегда имеет единственное решение 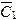и 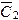. Рассмотрим два решения исходного линейного однородного дифференциального уравнения

y(x) и .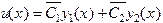

Эти решения удовлетворяют одному и тому же уравнению с одними и теми же начальными условиями 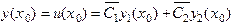. Следовательно, в силу теоремы единственности, эти решения совпадают при всех x, то есть

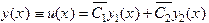
КОНЕЦ ДОКАЗАТЕЛЬСТВА.

ТЕОРЕМА 3. Всякое решение линейного неоднородного дифференциального уравнения имеет вид

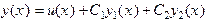
где

u(x) - частное решение линейного неоднородного уравнения

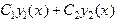- общее решение соответствующего однородного линейного уравнения ( 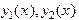- образуют Ф.С.Р.)

ДОКАЗАТЕЛЬСТВО. Пусть y(x) есть произвольное решение линейного неоднородного дифференциального уравнения

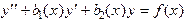
и u(x) есть некоторое частное решение этого же уравнения

.

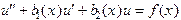Вычитая из первого уравнения второе, получим

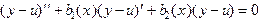
Тогда, из теоремы 2, получим 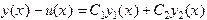, что и требовалось доказать.

КОНЕЦ ДОКАЗАТЕЛЬСТВА.

Из теоремы 2 ясно, что если известна Ф.С.Р., то можно найти любое решение линейного дифференциального уравнения. В общем случае неизвестен метод нахождения Ф.С.Р. для любого линейного однородного дифференциального уравнения второго порядка. Однако, если известно одно решение, то можно построить второе решение, линейно независимое с первым, и, следовательно, оба решения тогда образуют Ф.С.Р. Мы приведем два метода нахождения второго фундаментального решения по известному первому.

МЕТОД 1. Пусть 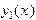есть решение уравнения 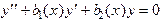. Будем искать второе решение в ви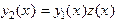де , где 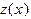- неизвестная функция. Подставляя в уравнение, получим

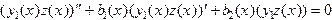
или

.

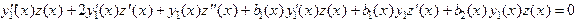Перегруппировав слагаемые, получим

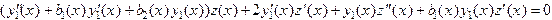
или, учитывая, что 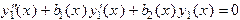, получим

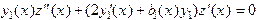
Пусть 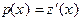, тогда получим

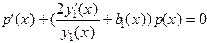
или разделяя переменные

.

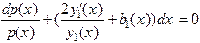Интегрируя, найдем

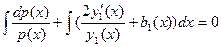
или

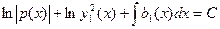
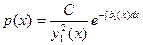
Откуда получаем

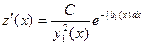
или

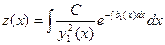
Отсюда окончательно получим

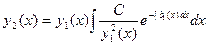
МЕТОД 2. Этот метод использует формулу Лиувилля. Действительно, решение уравнения Лиувилля

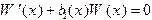
можно представить в виде

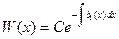
или

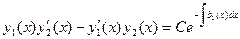
Разделив на 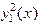, получим

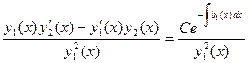
или

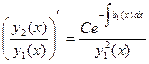
Отсюда получаем туже формулу для нахождения второго решения, что и в методе 1

.

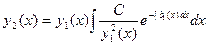Из вывода формулы следует, что определитель Вронского этих двух решений равен W(x).

ПРИМЕР 1. Пусть дано уравнение 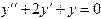. Это уравнение имеет решение 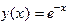. Найдем второе решение

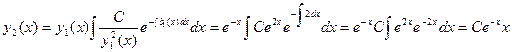
Здесь можно положить C=1.

Конец примера.