Самостоятельный электрический разряд в неоновой лампе

Неон, как и всякий газ, состоящий из нейтральных атомов, является изолятором. Необходимым условием возникновения электрического тока в газе является возникновение заряженных частиц в объеме газа, что можно осуществить путем ионизации атомов и молекул газа. При этом возникают электроны и положительно заряженные ионы атомов газа.

В зависимости от способа ионизации газа электрический разряд в газе называется несамостоятельным или самостоятельным.Несамостоятельным электрическим разрядом в газеназывается разряд, при котором ионизация осуществляется под действием высоких температур, рентгеновских или ультрафиолетовых лучей, излучения радиоактивных элементов, космических лучей (то есть под действием внешнего ионизатора). Разряд прекращается, если внешний ионизатор перестает действовать. Как правило, несамостоятельный разряд не сопровождается свечением.

Самостоятельный электрический разряд в газе осуществляется без воздействия внешнего ионизатора. Возникновение заряженных частиц в объеме газа происходит за счет столкновения электронов, которые приобрели достаточную скорость в электрическом поле, с нейтральными атомами и молекулами (ударная ионизация). При столкновении электрона с нейтральным атомом из атома «выбивается» электрон, то есть образуется еще один электрон и ион. Вторичные электроны, ускоряясь в электрическом поле, так же участвуют в ионизации атомов. В результате число носителей тока в газе возрастает практически в геометрической прогрессии. Вторичная электронная эмиссия – испускание электронов с поверхности катода при бомбардировке его положительными ионами дает начальный поток новых электронов. Начальные электроны для самостоятельного разряда всегда имеются в объеме любого газа, например, за счет космического излучения.

Для осуществления самостоятельного газового разряда кинетическая энергия ускоренного электрона должна быть равной энергии ионизации атомов газа ( )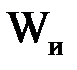

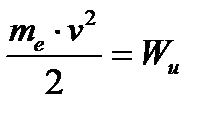(1)

где m_e - масса электрона, v - его скорость.

Кинетическую энергию электрона можно выразить через величину разности потенциалов, отвечающих двум последовательным соударениям его с атомами.

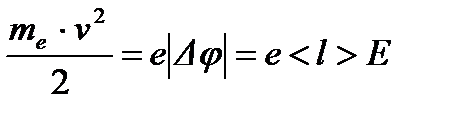, (2)

где е - заряд электрона, Δφ –разность потенциалов, < l > - средняя длина свободного пробега.

Таким образом, подставляя (2) в (1), получим

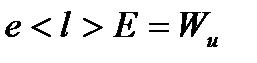. (3)

Напряжение зажигания самостоятельного газового разряда U₃ равно

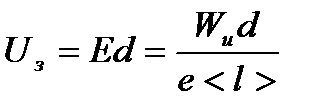, (4)

где d - расстояние между электродами неоновой лампы.

Как видно из уравнения (4), напряжение зажигания зависит от энергии ионизации молекул газа (от типа газа в баллоне), расстояния между электродами и длины свободного пробега электрона. С увеличением длины свободного пробега электрона (с уменьшением давления газа) напряжение зажигания уменьшается.

При атмосферном давлении для создания самостоятельного разряда требуются очень большие напряжения. В неоновой лампе такой разряд осуществляется при низком давлении (10 - 15 мм рт.ст.).

Самостоятельный разряд сопровождается оптическими явлениями - газ светится. Причинами свечения газа являются процессы: рекомбинации электронов с ионами; столкновение ионов с нейтральными атомами; столкновение электронов (прошедших расстояние, меньшее длины свободного пробега) с нейтральными атомами. Во всех этих процессах образуются атомы в возбужденном состоянии. При переходе их в основное состояние излучается квант света.

Свечение самостоятельного газового разряда, прилегающего к аноду, называется тлеющим разрядом.

Наиболее интересным оказалось то, что в работающей (зажженной) лампе потенциал между катодом и анодом изменяется неравномерно. Почти все падение потенциала, приложенного к лампе, приходится на небольшой участок вблизи катода. Эту часть напряжения называют катодным падением потенциала.

Светящаяся газоразрядная плазма, примыкающая к аноду и называемая положительным столбом, имеет высокую концентрацию электронов и положительно заряженных ионов. Поэтому положительный столб выполняет роль проводника, соединяющего анод с областью катодного падения потенциала.

Основные процессы, необходимые для поддержания тлеющего разряда, происходят в его катодной части. Поскольку в рабочем состоянии лампы напряженность электрического поля в катодной части увеличивается при заданном напряжении зажигания на лампе, то условие (3) будет выполняться при меньшем напряжении на лампе относительно напряжения зажигания. То есть напряжение гашения на лампе U_г должно быть меньше напряжения зажигания U_з.

Рассмотрим работу релаксационного генератора, схема которого приведена на рисунке 3.

При замыкании ключа К конденсатор медленно заряжается от источника с э.д.с. ε = U₀.

Напряжение на электродах лампы медленно возрастает. В момент, когда напряжение на конденсаторе достигает значения U_з , лампа зажигается, через нее идет ток. При этом происходит разряд конденсатора. Когда разность потенциалов на электродах лампы упадет до значения U_Г, лампа гаснет. Конденсатор заряжается снова. Таким образом, лампа периодически вспыхивает через определенные промежутки времени Т. Релаксационный генератор описанного типа будет источником пилообразного напряжения. Найдем зависимость между Т и параметрами генератора R, C, U_з и U₀.

По закону Ома для неоднородного участка цепи (ток через конденсатор не идет!):

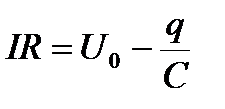, (5)

где q – заряд конденсатора.

По первому правилу Кирхгофа (закон сохранения заряда):

J = J₁ + J₂. (6)

Исключая из (5) и (6) токи J и J₂ , получим:

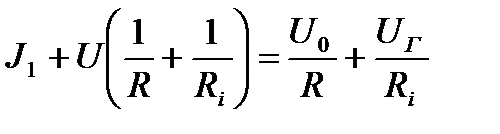. (7)

Так как .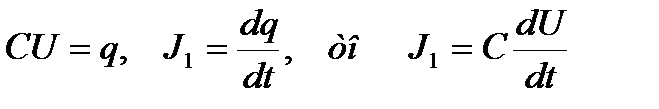

Следовательно, уравнение (7) примет вид:

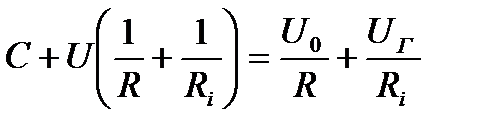. (8)

Решением этого дифференциального уравнения является

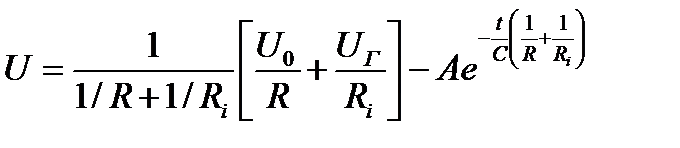, (9)

где А – постоянная интегрирования.

В схеме (см. рис.3а) происходит чередование двух основных стадий – стадия накопления в емкости С энергии электрического поля и стадии релаксации, когда конденсатор освобождается от значительной доли запасенной энергии электрического поля (она рассеивается в неоновой лампе). По форме, колебания близки к пилообразным. Такие автоколебания, резко отличающиеся от синусоидальных, называются релаксационными.

Определим период релаксационных колебаний. Период колебаний Т складывается из времени зарядки конденсатора t_з и времени его разрядки t_р до напряжения U_Г : T = t_з + t_р . Причем t_з = t_г - t₁ . Известно, что напряжение на конденсаторе емкостью С, заряжающемся от источника с э.д.с. ε = U₀ меняется со временем по формуле (показать самостоятельно):

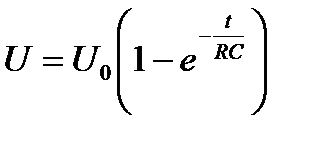. (10)

Величина RC называется постоянной времени цепи.

Используя (10), запишем формулы для U_з и U_Г :

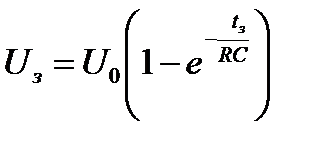и .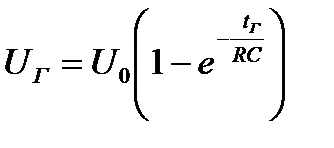

Получив из этих формул t_з и t_Г и подставив их в выражение t_з = t_г - t₁ , найдем :

.

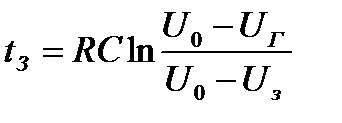Таким образом, время зарядки конденсатора определяется постоянной времени RC. Время разрядки определяется постоянной времени R_iC. Обычно R_i << R , и, следовательно, t_з >> t_р . Поэтому

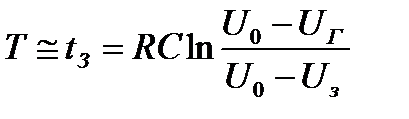. (11)