Примеры рефлексивных отношений
Доказательство
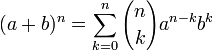
Докажем это равенство индукцией по n:
База индукции: 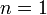
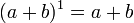
Шаг индукции: Пусть утверждение для 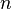 верно:
верно:
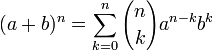
Тогда надо доказать утверждение для 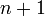 :
:
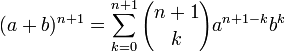
Начнём доказательство:
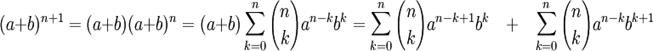
Извлечём из первой суммы слагаемое при 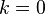
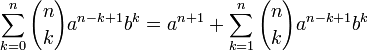
Извлечём из второй суммы слагаемое при 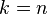
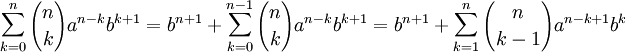
Теперь сложим преобразованные суммы:
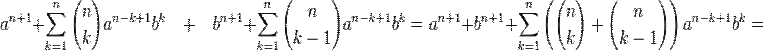
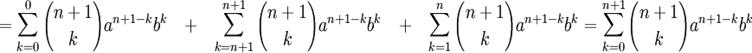
Что и требовалось доказать
Тема 2. Алгебра множеств
6. Понятия множества, подмножества, равенства множеств. Способы задания множеств. Операции над множествами. Соотношения между операциями. Способы доказательства соотношений между операциями.
Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).
Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.
Множество  является подмножеством множества
является подмножеством множества  , если любой элемент, принадлежащий
, если любой элемент, принадлежащий  , также принадлежит
, также принадлежит  .
.
Два множества  и
и  могут вступать друг с другом в различные отношения.
могут вступать друг с другом в различные отношения.
·  включено в
включено в  , если каждый элемент множества
, если каждый элемент множества  принадлежит также и множеству
принадлежит также и множеству  :
:
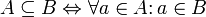
·  включает
включает  , если
, если  включено в
включено в  :
:
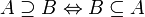
·  равно
равно  , если
, если  и
и  включены друг в друга:
включены друг в друга:
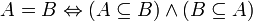
·  строго включено в
строго включено в  , если
, если  включено в
включено в  , но не равно ему:
, но не равно ему:
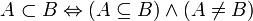
·  строго включает
строго включает  , если
, если  строго включено в
строго включено в  :
:
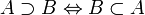
·  и
и  не пересекаются, если у них нет общих элементов:
не пересекаются, если у них нет общих элементов:
 и
и 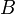 не пересекаются
не пересекаются 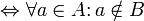
·  и
и  находятся в общем положении, если существует элемент, принадлежащий исключительно множеству
находятся в общем положении, если существует элемент, принадлежащий исключительно множеству  , элемент, принадлежащий исключительно множеству
, элемент, принадлежащий исключительно множеству  , а также элемент, принадлежащий обоим множествам:
, а также элемент, принадлежащий обоим множествам:
 и
и 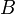 находятся в общем положении
находятся в общем положении 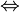
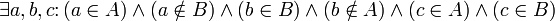
Сравнение множеств
Множество  содержится во множестве
содержится во множестве  (множество
(множество  включает множество
включает множество  ), если каждый элемент
), если каждый элемент  есть элемент
есть элемент  :
:
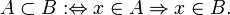
В этом случае  называется подмножеством
называется подмножеством  ,
,  — надмножеством
— надмножеством  . Если
. Если 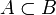 и
и 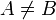 , то
, то  называется собственным подмножеством
называется собственным подмножеством  . Заметим, что
. Заметим, что 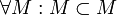 . По определению
. По определению 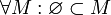 .
.
Два множества называются равными, если они являются подмножествами друг друга:
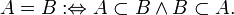
Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:
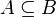
Операции над множествами
Бинарные операции
Ниже перечислены основные операции над множествами:
· пересечение:
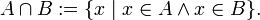
· объединение:
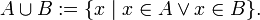
Если множества  и
и  не пересекаются,то
не пересекаются,то 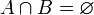 . Их объединение обозначают также:
. Их объединение обозначают также: 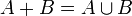 .
.
· разность (дополнение):
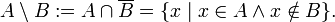
· симметрическая разность:
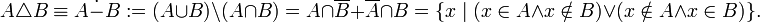
· Декартово или прямое произведение:
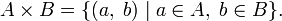
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Унарные операции
· Абсолютное дополнение:
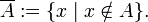
Операция дополнения подразумевает некоторый универсум (универсальное множество 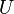 , которое содержит
, которое содержит  ):
):
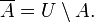
Относительным же дополнением называется А\В (см.выше):
· Мощность множества:
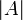
Результатом является кардинальное число (для конечных множеств — натуральное).
· Множество всех подмножеств (булеан):
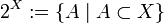
Обозначение происходит из того, что 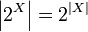 в случае конечных множеств.
в случае конечных множеств.
7. Булева алгебра всех подмножеств некоторого множества. Аксиомы булевой алгебры. Примеры алгебраического доказательства некоторых соотношений между операциями теории множеств из аксиом.
Аксиома коммутативности: x + y = y + x.
Аксиома ассоциативности: (x + y) + z = x + (y + z).
Уравнение Хантингтона: n(n(x) + y) + n(n(x) + n(y)) = x.
ассоциативность
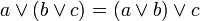
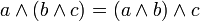
коммутативность
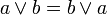
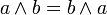
законы поглощения
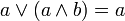
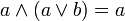
дистрибутивность
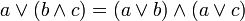
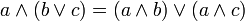
дополнительность
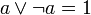
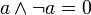
8. Теоретико-множественные средства моделирования. Понятие произведения множеств A x B. Теорема о числе элементов в A x B для конечных множеств A и B с доказательством методом полной математической индукции.
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.
Пусть 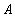 и
и 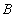 - множества. Выражение вида
- множества. Выражение вида 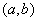 , где
, где 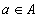 и
и 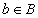 , называется упорядоченной парой. Равенство вида
, называется упорядоченной парой. Равенство вида 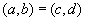 означает, что
означает, что 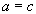 и
и 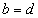 . В общем случае, можно рассматриватьупорядоченную n-ку
. В общем случае, можно рассматриватьупорядоченную n-ку 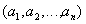 из элементов
из элементов 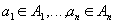 . Упорядоченные n-ки иначе называютнаборы или кортежи.
. Упорядоченные n-ки иначе называютнаборы или кортежи.
Декартовым (прямым) произведением множеств 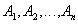 называется множество упорядоченных n-ок (наборов, кортежей) вида
называется множество упорядоченных n-ок (наборов, кортежей) вида
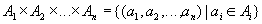
Степенью декартового произведения 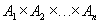 называется число множеств n, входящих в это декартово произведение.
называется число множеств n, входящих в это декартово произведение.
Замечание. Если все множества 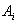 одинаковы, то используют обозначение
одинаковы, то используют обозначение
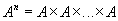 .
.
9. Понятие множества всех подмножеств P(M) множества M. Число элементов в P(M) для конечного множества M (с доказательством).
10. Понятие отношения и его теоретико-множественная модель. Определение свойств бинарных отношений: симметричность, рефлексивность, транзитивность. Примеры отношений. Определение отношения порядка. Примеры отношений порядка: больше или равно на числах, быть подмножеством на множествах, лексикографический порядок на словах.
Рефлексивное отношение
В математике бинарное отношение 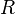 на множестве
на множестве 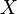 называется рефлексивным, если всякий элемент этого множества находится в отношении
называется рефлексивным, если всякий элемент этого множества находится в отношении 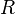 с самим собой.
с самим собой.
Формально, отношение 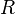 рефлексивно, если
рефлексивно, если 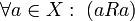 .
.
Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент имеет петлю — дугу (х, х).
Если это условие не выполнено ни для какого элемента множества 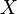 , то отношение
, то отношение 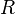 называется антирефлексивным.
называется антирефлексивным.
Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).
Формально антирефлексивность отношения 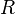 определяется как:
определяется как: 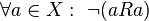 .
.
Если условие рефлексивности выполнено не для всех элементов множества 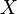 , говорят, что отношение
, говорят, что отношение 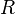 нерефлексивно.
нерефлексивно.
Примеры рефлексивных отношений
· отношения эквивалентности:
· отношение равенства 
· отношение сравнимости по модулю
· отношение параллельности прямых и плоскостей
· отношение подобия геометрических фигур;
· отношения нестрогого порядка:
· отношение нестрогого неравенства 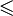
· отношение нестрогого подмножества 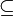
· отношение делимости 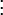
В математике бинарное отношение 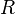 на множестве X называется симметричным, если для каждой пары элементов множества
на множестве X называется симметричным, если для каждой пары элементов множества 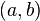 выполнение отношения
выполнение отношения 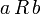 влечёт выполнение отношения
влечёт выполнение отношения 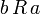 .
.
Формально, отношение 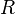 симметрично, если
симметрично, если 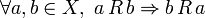 .
.
Антисимметричность отношения не является антонимом симметричного отношения. Оба свойства для некоторых отношений выполняются одновременно, а для некоторых не выполняется ни одно.
Примеры
Любое отношение эквивалентности, по определению, является симметричным (а также рефлексивным и транзитивным). Также симметрично отношение связи вершин графа (неориентированного).
Не являются симметричными (за исключением случая тождественной ложности отношения) отношения порядка (как полного, так и частичного), а также отношение следования вершин ориентированного графа. Однако, отношение сравнимости для частичного порядка является, по построению, симметричным (хотя, в отличие от самого́ порядка, не транзитивным).
Матрица симметричного отношения симметрична относительно главной диагонали (совпадает с транспонированной). Если в графе симметричного отношения существует связь между двумя вершинами, то существует и обратная связь.
Транзитивность
В математике бинарное отношение 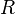 на множестве
на множестве 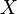 называется транзитивным, если для любых трёх элементов множества
называется транзитивным, если для любых трёх элементов множества  выполнение отношений
выполнение отношений 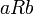 и
и 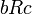 влечёт выполнение отношения
влечёт выполнение отношения 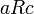 .
.
Формально, отношение 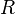 транзитивно, если
транзитивно, если 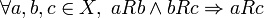 .
.
Примеры
· Равенство: 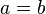 и
и 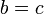 , значит
, значит  (на самом деле, отношение равенства вместе с отношением эквивалентности и параллельности прямых обладает более сильным свойством также ещё и «равенства третьему» по причине своей симметричности)
(на самом деле, отношение равенства вместе с отношением эквивалентности и параллельности прямых обладает более сильным свойством также ещё и «равенства третьему» по причине своей симметричности)
· Отношение порядка: 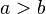 и
и 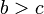 , значит
, значит 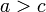 или нестрогого порядка:
или нестрогого порядка:  и
и 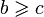 , значит
, значит 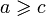
· Параллельность прямых: 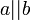 и
и 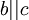 , значит
, значит 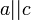 (см. примечание к «равенству чисел»)
(см. примечание к «равенству чисел»)
· Импликация: 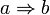 и
и 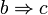 , значит
, значит 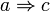
· Эквивалентность: 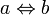 и
и 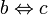 , значит
, значит 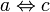 (см. примечание к «равенству чисел»)
(см. примечание к «равенству чисел»)
· Включение подмножества: если b является подмножеством a, и в свою очередь c является подмножеством b, тогда c является подмножеством a
· Делимость: если a делится на b, и b делится на c, тогда a делится на c.
· Отношение следования вершин ориентированного графа: если вершина 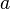 достижима из вершины
достижима из вершины  , а вершина
, а вершина  , в свою очередь, — из
, в свою очередь, — из  , то
, то 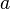 достижима из
достижима из  .
.
Примеры отсутствия транзитивности (встречаются, когда логические высказывания связаны не арифметическими отношениями или их эквивалентами в языке, а другими смысловыми отношениями):
· Игра «Камень, ножницы, бумага»: Камень сильнее Ножниц; Ножницы сильнее Бумаги; однако Камень не сильнее Бумаги ( 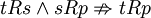 ). Здесь "сильнее" не имеет буквального значения, поскольку "сила" Бумаги в том, что она просто обертывает Камень.
). Здесь "сильнее" не имеет буквального значения, поскольку "сила" Бумаги в том, что она просто обертывает Камень.
· В круговом турнире часто бывает ситуация, когда команда A победила команду B, команда B — команду C, а C — A. Следовательно, в таком турнире отношение «победа» является нетранзитивным и не имеет эквивалента арифметической операции или арифметического отношения.
· Отношение связи вершин граф-схемы алгоритма: например, если в граф-схеме алгоритма имеет место альтернативное ветвление, начинающееся условной вершиной 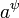 , и две вершины
, и две вершины 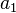 и
и 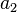 , входящие в состав различных альтернативных ветвей ветвления, то вершина
, входящие в состав различных альтернативных ветвей ветвления, то вершина 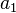 связана с
связана с 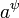 ,
, 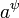 связана с
связана с 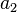 , однако вершины
, однако вершины 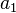 и
и 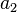 не связаны (они либо параллельны, либо альтернативны).
не связаны (они либо параллельны, либо альтернативны).
· Отношение параллельности вершин параллельной граф-схемы алгоритма: например, если в составе параллельного фрагмента алгоритма в одной из ветвей находится вершина 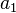 , а другая представлена альтернативным ветвлением с двумя ветвями, одна из которых содержит вершину
, а другая представлена альтернативным ветвлением с двумя ветвями, одна из которых содержит вершину 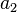 , а другая —
, а другая — 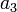 , то вершины
, то вершины 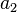 и
и 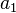 находятся в отношении параллельности, также как и вершины
находятся в отношении параллельности, также как и вершины 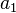 и
и 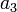 , однако вершины
, однако вершины 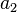 и
и 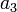 не параллельны (они находятся в отношении альтернативы).
не параллельны (они находятся в отношении альтернативы).
· Отношение альтернативы вершин граф-схемы алгоритма: например, если в составе альтернативного фрагмента алгоритма одна из ветвей представлена вершиной 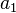 , а другая включает последовательно выполняемые вершины
, а другая включает последовательно выполняемые вершины 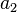 и
и 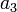 , то вершины
, то вершины 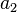 и
и 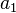 находятся в отношении альтернативы, что справедливо и для вершин
находятся в отношении альтернативы, что справедливо и для вершин 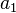 и
и 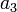 , однако вершины
, однако вершины 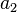 и
и 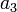 не состоят в отношении альт
не состоят в отношении альт
11. Отношение эквивалентности. Определение фактор множества по отношению эквивалентности. Примеры.
Отношение эквивалентности
У этого термина существуют и другие значения, см. Эквивалентность.
Отношение эквивалентности ( 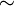 ) на множестве
) на множестве 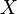 — это бинарное отношение, для которого выполнены следующие условия:
— это бинарное отношение, для которого выполнены следующие условия:
1. Рефлексивность: 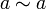 для любого
для любого 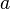 в
в 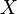 ,
,
2. Симметричность: если  , то
, то 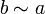 ,
,
3. Транзитивность: если  и
и 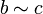 , то
, то 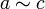 .
.
Запись вида «  » читается как «
» читается как « 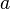 эквивалентно
эквивалентно  ».
».
Связанные определения
· Классом эквивалентности 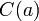 элемента
элемента 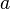 называется подмножество элементов, эквивалентных
называется подмножество элементов, эквивалентных 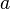 . Из вышеприведённого определения немедленно следует, что, если
. Из вышеприведённого определения немедленно следует, что, если 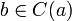 , то
, то 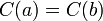 .
.
Множество всех классов эквивалентности обозначается 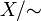 .
.
· Для класса эквивалентности элемента 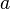 используются следующие обозначения:
используются следующие обозначения: 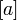 ,
, 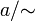 ,
, 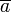 .
.
· Множество классов эквивалентности по отношению 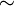 является разбиением множества.
является разбиением множества.
