Математиканы оқытудағы ғылыми таным әдістері. Бақылау және тәжірибе

Лекция

Математиканы оқытудағы проблемалық және эвристикалық әдістер.

Жоспары:

1. Проблемалық оқыту

2. Эвристикалық әдіс

3. Бағдарламалық оқыту

4. Практикалық және лабораториялық жұмыстар.

1. Проблемалық оқыту. Проблемалық оқыту шығармашылық (творчестволық), тапқыр (эвристикалық) ойлауға сүйенеді. Мұндай ойлау әсіресе стандартты емес есептерді шешуде қажет болады. Сонымен бірге проблемалық әдіс математикалық теорияны оқып, үйренуде аса тиімді. Сондықтан да проблемалық әдіс болашақта орта мектепте математиканы оқытудың негізгі әдістерінің бірі болуға тиіс.

Проблемалық оқыту теориясы көптеген педагогтар еңбектерінде (М.И.Махмутов, А.М.Матюшхин, В.Оконь т.б.) терең зерттеле бастады. Бұл теорияның ең басты ұғымдары “проблема” (оқулық) және “проблемалық жағдай” (ситуация) ұғымдары болып табылады. Проблемалық жағдай оқушыны жаңа білім алуға итермелейтін ойлау әрекетіне бастайды, оған жағдай туғызады.

Оқулықтағы математикалық есептер мынадай екі жағдайда проблемалық жағда йға душар етеді: 1) егер оның шарты мен талабының арасына ойлау субъектісі болып саналатын оқушы адам тұрса; 2) ол адам бұл есепті қалай шешуді білмесе.

Кез келген есеп білмегендер үшін ғана проблема болады, ал оның шешуін білетіндер үшін ол ешқандай проблема болмайды.

Оқушыларда белгілі бір проблемалық жағдай қоюдың (туғызудың) негізгі үш тәсілін көрсетуге болады.

1. Мұғалімнің өзі тікелей қоятын проблема. 2. Проблеманы қою және оны тұжырымдау. 3. Проблеманы сипаттайтын шарттарды қарастыру. 4. Қойылған проблеманы шешу: а) проблеманы талдап, тексеру және оны шешудің көңілге қонымды бағыттарын іздестіру; ә) проблеманы шешуге қажетті мағлұматтарды іріктеу және оларды бір жүйеге келтіру; б) қабылданған шешу жоспарын нақтылау (детализация). 5. Алынған жауаптың дұрыстығын негіздеу. 6. Проблеманы шешу жолын және оның нәтижесін зерттеу және жаңа білімді айқындау. 7. Жаңа білімді арнайы іріктеп алынған есептерді шешуге практикалық қолдану. 8. Қойылған проблеманы мүмкіндігінше кеңейту және жалпылық жолдарын іздестіру. 9. Проблеманың алынған шешуін қарастыру; бұдан басқа да тиімді және сындарлы жолдарын іздестіру. 10. Жасалынған жұмысқа қорытынды жасау.

Бұл жоспарды жүзеге асыруда оқушылар барынша көп қатыстырылып, мұғалімнің өзі мүмкіндігінше аз араласуға тырысуы қажет.

Проблемалық сабақты ұйымдастыруда, оқу проблемасының нақты сипатына сәйкес бұл сүлбелік жоспар кейде толық, кейде ішінара орындалуы мүмкін, кейбір пункттерді біріктіріп жіберуге тура келеді т.б.

Сабақ үстінде оқушылар алдына қойылатын проблемалар сан алуан болып келеді. Жаңа тақырыпқа кіріспе, есепті жаңа тиімділік әдіспен шешу, белгілі материалды жаңа оқу материалымен байланыстыру т.б.

Мәселен, “геометриялық денелердің” (призма мен пирамида), көлемдері мен беттерінің ауданы өзгере ме?

Математикалық шығармашылыққа бейім шәкірттерге арнайы лайықтап алынған проблемалық сипаттағы есептер қоюда мынадай шарттарды ескеру қажет.

1. Шәкірттер проблемалық мазмұнды тапсырманы үй жағдайында белгілі бір азды-көпті мерзім ішінде (1-2 апта) орындаулары қажет.

2. Проблемалық сипаттағы тапсырмаларды орындаудың жолдары шешу деңгейі, проблеманы игерудің терендігін, жалпылау дәрежелері және дамыту мүмкіндіктері тұрғысынан түрліше болып келуі тиіс.

3. Проблемалық сипаттағы тапсырмалар мазмұны жөнінен танымал болмайтын болып келіп, оны шешу үшін оқушылар дайын әдеби құралдарды аз пайдаланып, өз беттерінше, өз күштерімен әрекеттенетіндей етіліп құрастырылуы қажет.

4. Оқушылардың жеке ерекшеліктері мен қабілеттерін қанағаттандыру үшін тапсырмаларды мектеп математика курсының әр түрлі тарауларынан іріктеп алған жөн.

5. Проблемалық сипаттағы тапсырмалар сынып ұжымына беріледі.

6. Шәкірттердің проблемалық тапсырмалар жөніндегі зерттеулері арнайы реферат түрінде жазылып, сыныпта немесе математика үйірмесінде талқыланғаны жөн. Нақты мысалдар келтірейік.

Оқушы квадрат тендеу тақырыбын өтіп болған соң биквадрат теңдеуді өту кезінде төмендегі проблемалық ахуалдарды шығарып алуы мүмкін.

М: 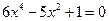тендеуін қандай теңдеу деп атаймыз?

О: 4-дәрежелі теңдеу деп аталады.

М: Дұрыс, олай деп айтуға да болады, бірақ математикада мұндай түрдегі теңдеулер биквадрат теңдеулер деп аталады, олар жалпы түрде былайша жазылады: 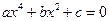. Жарайды, мұндай түрдегі теңдеулер қандай әдіспен шешіледі?

О: Біз мұндай теңдеулерді шешпегенбіз. Міне осы жерде өтілетін тақырыптың материалымен оқушылар арасында проблемалық ситуация пайда болады.

М: 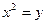деп белгілесек, 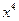-ті қандай белгілеуге болады?

О: Көмекші белгісіз енгізу тәсілін қолданып 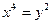тең болатындығына оқушылар көз жеткізеді.

М: Бұл теңдеуді жаңа белгілеулер енгізу арқылы қандай түрде жазуға болады?

О: .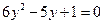

М: Бұл шыққан теңдеу қандай теңдеу деп аталатын?

О: Толық квадрат теңдеу деп аталады.

М: Бұл теңдеуді қайтіп шешеміз?

О: Толық квадрат теңдеудің жалпы формуласын табу формуласына сүйеніп табамыз:

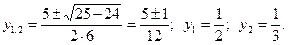
М: Біз қазір теңдеуді шешіп, қайсы белгісізді таптық?

О: Белгісіз у-ті таптық.

М: Нені табуымыз керек еді?

О: х-ті табуымыз керек еді?

М: х-ті калай тамабыз?

Міне осы жерде белгісіз х-ті табу үшін көпшілік оқушылар арасында тағы да, проблемалық ситуация пайда болады. Оқушылар белгісіз х-ті өздері табуы мүмкін, нашар оқушыға мұғалімнің өзі жәрдемдеседі:

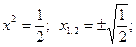
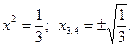
Демек, теңдеу 4-ші дәрежелі болатындықтан біз 4 шешімді таптық. Бұл есепті шешіп болғаннан кейін 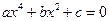биквадрат теңдеуінің жалпы шешімін оқушылар мұғалім көмегімен өздері таба алады:

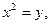
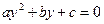
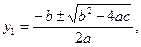
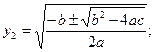
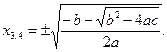
Біз жоғарыда қазіргі кезде орта мектеп тәжірибесінде кең қолданылып жүрген негізгі оқу әдістеріне тоқталдық. Қандай материалды өту кезінде қандай әдісті қолдану мәселесін мұғалім әр сабаққа дайындалу барысында өзі шешеді. Бұл тұрғыдан ескеретін бір жайт қарастырылған әдістердің қай-қайсысы болмасын барлық жағдайға лайық, бірден-бір әмбебап әдіс бола алмайды.

2. Эвристикалық әдіс.Оқытудағы эвристикалық әдіс деп әдістемеде негізінен диалогиялық (сұрақ-жауап) формадағы эвристикалық әңгімені түсінеді. Мұнда мұғалім оқушыларға білімді, ұғымды бірден дайын түрінде бермей, өз орнымен қойылған сұрақтар арқылы оларда бұрын қалыптасқан білімдері мен бақылаулары және өмір тәжірибесіне сүйеніп жаңа ұғымдарға, ережелерге, дәлелдеулерге және есептің шешуіне өздерін келтіру керек (бағыштау керек). Эвристикалық әңгіме оқытуда орын алып келген жалаң, жаттау мен догматизмге қарсы бағытталған оқушылардың ізденімпаздығын, олардың өз бетінше ойлау қабілетін арттыруды көздейтін прогрессивтік әдіс болып табылады. Эвристикалық әңгіме қойылатын сұрақтар ішінде оқушылар бірден дайын жауап таба алмайтындай проблемалық сауалдар кездеседі. Бұрын үйретілген мәселелерді еске түсіріп, жаңғыртуға арналған сұрақтар мұнда шешуші рөл атқармайды, олар тек әлі белгісіз тың сұрақтарға жауап беруге, шешуге көмекші болады. Тек өткенді қайталау, жаңғыртуға арналған әңгіме эвристикалық әңгімеге жатады, оны қатехиздік әңгіме дейді.

Қазіргі дидактиканың барлық талабын қанағаттандыра отырып, эвристикалық әңгіме оқушыларға сабақ барысында танып білгізудің ең маңызды және тиімді әдістерінің қатарына жатады. Ол қазіргі жағдайда V-IX сыныптарда математикадан жаңа материал өтуде және жаппай есеп шығартуда негізгі әдіс болуы керек. Ол әрине, мұнда басқа оқыту әдістерімен ұштастыра пайдаланылуы тиіс. Бұл тұрғыда алдыңғы қатарлы тиімді әдістер болып табылатын проблемалық-бағдарламалық жаңа әдістер алдыңғы кезекке шығады. Эвристикалық әңгіме синтетикалық әдістерден гөрі аналитикалық әдістермен жақсы үйлеседі.

Эвристикалық әңгіме-сұрақтар жүйесі бірсыпыра шарттарды қанағаттандыруы қажет: сұрақтар логикалық жағынан жүйелі қысқа, дәл болуы; екі-ұшты, дүдәмәл болмауы, жауабы оп-оңай болмауы және оқушылардың көпшілігінің жан-жақты ойлауына кең жол алуы т.б. Ал бұған берілетін оқушының жауабы дәл және толық, барлық сыныпқа түсінікті болуы қажет. Жауапқа көп оқушы қатысқаны дұрыс болады.

Енді жоғарыдағы айтылған пікірлердің дәлелі ретінде төмендегі теңдеу мен мәселе есепті эвристикалық тәсілмен шешу әдісін көрсетеміз.

1. Мына теңдеуді 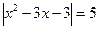эвристикалық әдіспен шешу керек.

Бұл теңдеуді эвристикалық әдіспен шешу кезіндегі оқушы мен мұғалім арасындағы сұхбатты келтіреміз.

М: 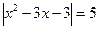теңдеуі қалай шешіледі?

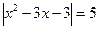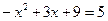О: Бұл теңдеуді шешу үшін оны және теңдеулер түрінде жазып аламыз.

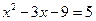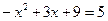М: және теңдеулерін қандай ережеге сүйеніп жаздыңдар?

О: Егер бізге 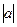саны берілген болса, онда модульдың анықтамасы бойынша:

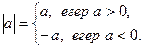
М: Жарайды, онда шыққан теңдеулер қалай шығарылады?

О: , ,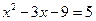

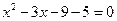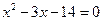
М: 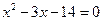теңдеуін қандай формуланы пайдаланып шешеміз?

О: 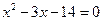теңдеуі 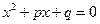түріне келді, бұл келтірілген квадрат теңдеу.

М: Кім айтады, 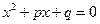теңдеуінің жалпы шешімі қандай формуламен анықталатын еді?

О: 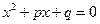теңдеуінің шешімі

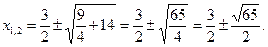
М: 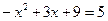тендеуі қалай шешіледі?

О: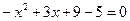

М: Енді не істейміз?

О: Ұқсас мүшелерін біріктіреміз: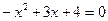

М: Белгісіз х-тің алдында тұрған минус таңбасын, оң таңбаға айналдыру үшін не істейміз?

О: Теңдіктің екі жағында бірдей (-1)-ге көбейтеміз:

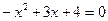(-1), .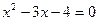

Бұл теңдеу де жоғарыдағы тәсілмен шешіледі:

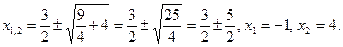
Жауабы: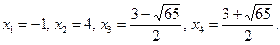

2-мысал. Енді темендегі мәселе есепті эвристикалық әдіспен шығарайық.

Есеп. Ара қашықтығы 60 км болатын А пунктінен В пунктіне бір мезгілде екі велосипедші жолға шықты. Олар бір мезгілде В пунктіне келулері тиіс еді. Бірінші велосипедші болса әр сағатына 2 км кем жүргендіктен бір сағат кеш келді. Әрбір велосипедші қандай жылдамдықпен жүрген?

М: Есептің шарты қандай? Онда нелер берілген? Есептің шартында қандай шамалар қатыскан?

О: А және В пункттерінің ара қашықтығы 60 км екені берілген. Велосипедшінің жылдамдықтарының арасында және осы ара қашықтықты жүріп өтуге кеткен уақыттардың арасындағы айырма берілген. Бұл есептің шартында тездік, арақашықтық және уақыт шамалары берілген.

М: Есепте нені табу керек?

О: Есепте әрбір велосипедшінің жылдамдығын табуды сұрайды.

М: Бұл жылдамдықтарды табу үшін қандай формулаларды пайдаланамыз?

О: Бізге физика курсынан белгілі 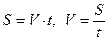формулаларын пайдаланамыз.

М: Есептің шартына қарай нені х арқылы белгілейміз.

О: А пунктінен В пунктіне қарай шыққан бірінші велосипедшінің жылдамдығын х км/сағ деп белгілейміз.

М: Егер біз бірінші велосипедшінің жылдамдығын х десек, екінші велосипедшінің жылдамдығын осы белгісіз шама арқылы өрнектей аламыз ба?

О: Иә, 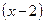км/сағ екінші велосипедшінің жүрген жылдамдығы болады.

М: А пунктінен В пунктіне дейінгі ара қашықтықты бірінші велосипедші қанша уақытта жүріп өтеді?

О: 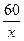сағатта.

М: А пунктінен В пунктіне дейінгі ара қашықтықты екінші велосипедші қанша уақытта жүріп өтеді?

О: 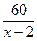сағатта.

М: Бұл велосипедшілердің 60 км ара қашықтықты жүріп өтуге кеткен уақыттары үшін қандай теңдеу құруға болады?

О: 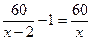теңдеуі арқылы.

М: Бұл теңдеуді қалай шешеміз?

О: Теңдеуді шешудің жалпы ережесі бойынша:

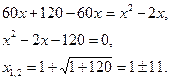
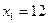км/сағ, 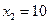км/сағ.

Демек, бірінші велосипедшінің жылдамдығы 12 км/сағ, екінші велосипедшінің жылдамдығы 10 км/сағ-қа тең болған.

Эвристикалық әдісті көп қолданып жүрген мұғалімдер тәжірибесі, оның оқушылардың оқу жұмысына деген көзқарасын өзгертетінін көрсетеді.

Эвристикаға “дәндеп” алған шәкіртке “дап-дайын” жоспармен жұмыс істеу қызық болмай қалады, жалықтырады. Сабақ кезінде немесе үй тапсырмасын орындау мезетінде болсын, мәселені шешу кілтін, есептерді шешудің жаңа жолдарын оқушылар өздері “ашуға” құмарлық пайда болады. Олар эвристикалық әдіс-айлалар қолданылатын жұмыстарға ынталы болады. Ал бұл сайып келгенде, шәкірттердің математикалық талғамын жақсартып, математиканың негіздерін саналы түрде игеруіне игі әсер етеді.

Эвристикалық әдісті қолданудағы бір кемшілік – ол қойылған оқулық проблеманы үйретуде мұғалімнің өзі айту (информациялық) әдісіне қарағанда уақытты көп алады. Сондықтан да оқытушының бұл әдісті сабақ сайын қолдануына мүмкіндігі бола бермейді. Оның үстіне қандай да бір тиімді әдіс болмасын, оны үнемі қолдана беру дұрыс емес, басқа әдістерді алмастырып отыру қажет.

3. Бағдарламалық оқыту.Математиканы оқыту әдістері кез келген басқа білім салалары сияқты үнемі даму, жетілу үстіндегі ғылым. Бұл әсіресе оқыту әдістемесіндегі орын алып отырған өзгерістерден анық байқалады. Кейінгі кезде математика педагогикасында жоғарыда айтылған дәстүрлі оқу, оқыту әдістерімен қатар және соларға ұштастырыла қолданылатын жаңа әдістер бой көрсетіп, кейбіреулері математиканы оқыту практикасында лайықты орын ала бастады.

Математиканы оқытудың қазіргі кездегі ең басты кемшіліктері мынадай:

1) Оқытудың барлық кезеңдерінде шәкірттердің білім алу белсенділігін арттыру. Мұнда мұғалімнің жәрдемімен шәкірттердің өздігінше білім алуына баса көңіл бөлінеді. 2) Оқу үрдісіне оқушылардың математикалық ойлауын интесивтендіру, яғни оларды математика саласы бойынша теориялық білім алу және рационал ойлаудың негізгі интенсивті әдістерін игеруге баулу.

Оқыту – мұғалім тарапынан оқыту, үйрету, ал шәкірт тарапынан оқу, үйренуді қамтитын екі жақты үрдіс. Сондықтан да оқыту жемісті болу үшін бұлар арасында әрқашан тура және кері байланыс орын алуы керек. Оқытушы оқу үрдісінің жүруін басқарып отыру үшін шәкірттен мұғалімге ол жөнінде ақпарат дер кезінде жетіп отыруы шарт. Тек осындай ақпаратты ескере отырып, мұғалім сабақ үстінде әр оқушының оқуына білікті түрде араласа алады. Бұл бағдарламалық оқыту идеясын туғызады. Бұл әдіс бойынша оқушы бағдарламаланған оқулықтағы немесе оқыту мәшинесіне енгізілген арнайы құрастырылған оқыту бағдараламасына сәйкес жұмыс істейді. Бағдарламада шәкірт өз жұмысының дұрыс-бұрыстығын бақылап отыруы үшін қойылған сұрақтардың жауаптары да келтіріледі. Бағдарламалық әдісті басқа әдістермен біріктіре отырып қолданудың бір түрі бағдарламалық картаны пайдадалану болып табылады. Бұл картада оқулықта келтірілген математиканың белгілі бір тарауын өз бетінше оқып игеруді жүзеге асыруды көздеген нұсқаулардың реттелген жүйесі келтіріледі. Бағдарламалық карта арқылы мектеп математика курсындағы белгілі бір тақырыпта көлемі шағын өз бетінше оқу барысында оқушы өз әрекетінің дұрыстығын дер кезінде бақылап отыруға мүмкіндік алады.

Қазір математикалық пәндер бойынша жоғары және орта мектептерге арналған бағдарламаланған оқулықтар мен материалдар дайындалып, олармен тиісті эксперименттер жүргізілуде.

Оқытатын бағдарлама сайып келгенде оқыту алгоритмі болады, ендеше бағдарламалық оқыту – оқу үрдісін алгоритмдеу проблемасымен тығыз байланысты болады.

Бағдарламалық оқытуды дамытып, мектеп практикасына енгізу оқытудың техникалық құралдары рөлін күшейте түседі. Мектептерде бағдарламаланған оқулықтарды кең қолдану мәшинелік оқытуды қолға алуға мүмкіндік береді (микропроцессорлар, ЭЕМ т.б.).

Сұрақтар:

1. Проблемалық оқыту

2. Эвристикалық әдіс

3. Бағдарламалық оқыту

4. Практикалық және лабораториялық жұмыстар.

Әдебиеттер:

1. Ә.Бидосов. Орта мектепте математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 224 б.

2.Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә С. Математиканы оқыту теориясы мен әдістемесі. – Алматы: Білім,1998. – 208 б.

3. Бейсеков Ж., Рахымбек Д., Шарипов Т.А. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. –Шымкент.2003-179 б.

Лекция

Математиканы оқытудағы ғылыми таным әдістері. Бақылау және тәжірибе

Жоспары:

1.Таным әдістері - оқыту әдістері

2. Бақылау

3. Экссперимент

2. Бақылау.Қандай ғылым болса да қарастырылып отырған объектілердің мәнін ашып, олардың қандай заңдылықтарға бағынатынын зерттейді. Объектілерді танып білу, оларды бақылау және оны сипаттау жұмыстарынан басталады.

Бақылау зерттелінетін объектілерді мақсатты және жүйелі түрде тікелей қабылдау арқылы зерттейтін әдіс. Психологтар объектілерді қабылдаудың мазмұны және бағыттылығы бізді қоршаған ақиқат дүние туралы адамның қандай білімдері, тәжірибесі бар екендігіне байланысты болатындығын анықтаған.

Бақылау – ақпарат алудың ең маңызды әдістерінің бірі, ал бақылау жүргізе білу зерттеушінің бағалы қасиеті. Сондықтан оқушылардың бақылау жасай алуын қалыптастырудың қажеттігі ешқандай күмән туғызбайды. Бақылау жасауды дұрыс ұйымдастыру оқушылардың математикалық деректерді табысты игеруіне жағдай жасайды, заңдылықтарды көре білуге және қорытынды тұжырымдап айтуына жәрдемдеседі. Л.Эйлер сандардың бізге белгілі қасиеттерінің көпшілігі, олардың дұрыстығын қатаң түрде дәлелдеуге мүмкіндігіміз жоқ, тек бақылау нәтижесінде ғана танып білуге болатын сандардың бізге етене таныс қасиеттері бар деген болатын.

Бақылауды мынадай жоспар бойынша жүргізуге болады:

1. Бақылаудың мақсатын анықтау.

2. Бақыланатын объектілердің маңызды (елеулі) қасиеттері мен ерекшеліктерін ашу.

3. Бақылау кезіндегі алынатын ақпараттарды есепке алып отыру тәсілдерін анықтау (сипаттау, сызбалар жасау, сандық мәндерді кестеге түсіру және т.б.).

4. Зерттелінетін объектілердің ерекшеліктері мен белгілері арасындағы өзара байланысты тағайындау.

5. Бақылау нәтижелеріне талдау жасау, қорытындылар тұжырымдау.

Математикада бақылауды пайдалануға мысалдар келтірейік.

1-мысал. 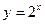көрсеткіштік функциясының қасиеттерін оқып үйренуде мынадай кесте құрастырылады.

х	-2	-1,75	-1,5	...			...
у	0,25	0,30	0,95	...			...

Кестеге қарап отырып оқушылар 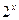өрнегінің мәні айнымалы 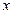-тің кез келген мәнінде оң болатындығын және 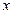-тің мәні артқан сайын функцияның мәні артатындығын көреді. Оқушылар 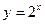функциясы рационал сандар жиынында оң және өспелі болатындығы туралы болжам жасайды да, ол қасиетті аналитикалық түрде дәлелдейді.

2-мысал. Алғашқы n натурал санның квадраттарының қосындысын табу керек.

Ш е ш у і. Алғашқы n натурал санның

1+2+3+4+...+ n

қосындысын мынадай формуламен табуға болады: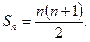

Алғашқы n натурал санның квадраттарының

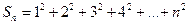
қосындысын табу үшін 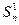және 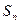қосындыларының кестесін құрастырайық:

								...
								...
								...

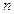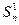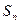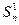және 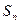мәндерінің өзгеруіне тікелей бақылау жасау нәтижесінде олардың арасындағы заңдылық бірден көрінбейді. Сонда кестедегі мәндердің 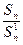қатынасын зерттеу керек деген болжам жасап көреді.

n=1,2,3,4,5,6,7 үшін 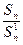қатынасының мәндері мынадай болады:

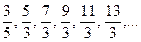
Сонымен 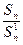қатынасын былайша жазуға болады:

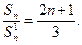
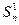мәні белгілі болғандықтан

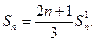
болады немесе

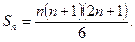
Сонымен алғашқы n натурал санының квадраттарының қосындысын жалпы мына түрде жазуға болады:

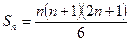(1)

Бұл формуланы бірнеше жеке жағдайларды қарастыру нәтижесінде алып отырмыз, сондықтан n-нің барлық мәндері үшін дұрыс екендігін дәлелдеуіміз немесе теріске шығаруымыз керек. Ол үшін математикалық индукция әдісі қолданылады. (1) формула n=1 үшін дұрыс, ал n=k үшін бұл формула дұрыс деп жориық, мұндағы k-кез келген натурал сан.

Сонда

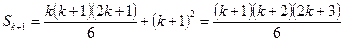
(1) формуласы n=k+1 үшін дұрыс екендігі шығады. Сонымен (1) формула n-нің барлық мәндері үшін дұрыс екен.

2. Эксперимент. Эксперимент(тәжірибе) – танып білудің ең тиімді әдістерінің бірі болып табылады.

Эксперимент(лат. experimentum – тексеріп, жасап (істеп көру, тәжірибе)) – зерттеушінің тікелей белсенді аралсуы арқылы зерттелетін объектінің қасиеттерін анықтау мақсатында әдейі арнап қажетті жағдайлар туғыза отырып танып білу әдісі.

Тану қызметінде орындалатын жұмыстың мазмұнына қарай эксперимент тексеруші жәнедемонстрациялаушы (иллюстрациялау) болып бөлінеді. Эксперимент объектінің тікелей өзін немесе оның моделін қарастыру арқылы жүзеге асырылады.

Ғылыми тануда ойлау арқылы жүргізілетін эксперимент ерекше орын алады. Бұл формальды-логикалық іс-әрекеттерді жүзеге асырып қана қоймай, объектінің бейнелері (образдары) мен модельдерін зерттеу нәтижесіндегі жаңа білімдерге жету қызметі болып табылады. Ойша эксперимент негізінде мынадай амалдар жүзеге асырылады.

1. белгілі бір ереже бойынша зерттелінетін объектінің ойша моделі құрылады, яғни идеалданған объект жасалынады;

2. модельге әсер ететін идеалданған жабдықтар мен құралдар құрылып, идеаландырылған шарттар да жасалынады;

3. шарттарды саналы түрде жоспарлы өзгерте отырып, салыстырмалы және еркін комбинациялау;

4. ойша эксперименттің барлық кезеңдерінде, ғылымда калыптасқан объективті заңдылықтарды саналы да дәл пайдалану, деректерді қолдану кезінде абсолюттік еркіндікке, негізсіз фантазияға жол бермеу.

Нақты (реальды) эксперименттің элементтері мыналар:

1. мәселені қою және болжам жасау;

2. объектілерді зерттеудің эксперименттік алғы шарттарын жасау;

3. салдарды белгілеу және оның себептерін тағайындау;

4. жаңа құбылыстарды және олардың ұқсастығын сипаттау.

Бақылау мен тәжірибе арқылы алгебралық заңдылықтарды да тағайындауға болады.

Есеп.Мұраттың қолындағы екі қапшықтың бірінде 5 кг картоп, екіншісінде 3 кг қияр бар. Келесі дүкенде помидор сатылып жатқандықтан ол қапшықтың біреуін босатуға мәжбүр болды. Қапшықты неше тәсілмен босатуға болады?

Бір қапшықты екі тәсілмен босатуға болады. Бірінші, картоптың үстіне қиярды (5кг+3кг); екінші, қиярдың үстіне картопты (3кг+5кг) салу керек. Екі жағдай да қапшықтағы картоп пен қияр 8 кг болып шығады. Демек, 5кг+3кг=3кг+5кг=8кг. Осындай бірнеше мысалдар (тәжірибе) келтіру арқылы қосылғыштардың орнын ауыстыруынан қосынды өзгермейтінін тағайындауға болады. Бұл ережені қорыта отырып, жалпы жағдайда (индукция арқылы) a+b=b+a екеніне көз жеткізуге болады.

Бақылау мен тәжірибе математикалық заңдылықтардың тек ең қарапайым түрлерін ғана көрсете алады, сондықтан оны математикалық фактілердің қатаң негіздемесі ретінде қабылдауға болмайды.

Сұрақтар:

Математиканы оқытудың ғылыми таным әдістері.

Математиканы оқытудағы бақылау.

Математиканы оқытудағы тәжірибе.

Әдебиеттер:

1. Ә.Бидосов. Орта мектепте математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 224 б.

2.Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә С. Математиканы оқыту теориясы мен әдістемесі. – Алматы: Білім,1998. – 208 б.

3. Бейсеков Ж., Рахымбек Д., Шарипов Т.А. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. –Шымкент.2003-179 б.