Изучение колебательного движения

ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

Учебно-методическое указание для студентов 1 курса физического факультета

(1.1)

(1.1)

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА МЕХАНИКИ МНОГОФАЗНЫХ СИСТЕМ

ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

Учебно-методическое указание для студентов 1 курса физического факультета

Тюмень, 1995.

(1.1)

1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Колебания широко распространены в природе и технике. Простейшими являются гармонические колебания, т.е. такие колебания, при которых некоторая величина, характеризующая это движение (например, смещение маятника относительно положения равновесия) изменяется со временем по синусоидальному закону. Кинематические соотношения, описывающие гармонические колебания, легко получить, анализируя следующую модель (рис 1,1). Пусть радиус-вектор R равномерно вращается с постоянной угловой скоростью ω₀ против часовой стрелки. В момент начала наблюдения радиус-вектор образовал угол α с осью ОХ. Координаты конца радиус-вектора (точка А) соответственно равны:

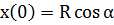
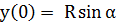
В любой дальнейший момент времени координаты x и y будут определяться соотношениями:

(1.1)

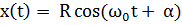
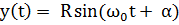
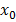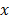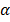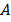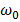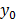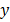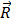Рис. 1.1

т.е. координаты x и y точки A меняются по гармоническому закону. Соотношения вида (1.1) Называются уравнениями гармонических колебаний.

Величина, стоящая перед синусом или косинусом, R называется амплитудой, (ωt+α) – фаза колебания, α - начальная фаза, ω - циклическая частота, T=2π/ω₀ – период колебаний.

Пусть материальная точка совершает колебательное движение вдоль оси X. Тогда зависимость координаты x от времени будет определяться выражением (1.1), где R целесообразно заменить на x₀ – максимальное смещение относительно положения равновесия. Другие кинематические величины (скорость и ускорение) определяются как обычно в механике путем дифференцирования координаты по времени:

(1.2)

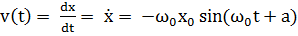
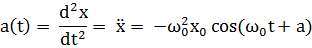
Графики x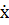(t), (t), 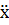(t) в зависимости от времени представлены на рис 1.2.

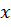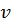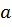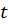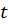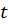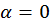Рис. 1.2

Очевидно, что скорость и ускорение колеблющейся точки также меняются по гармоническому закону. Из анализа формул (1.2) и соответствующих им графиков рис.1.2 следует, что скорость смещена по фазе на π/2 относительно координаты, а ускорение смещено по фазе на π/2 относительно скорости и на π относительно координаты точки.

С точки зрения динамики, колебательные движения возникают в системах, имеющих положение устойчивого равновесия. При небольших отклонениях от этого положения в системе возникают силы, стремящиеся вернуть ее в положение равновесия. Примером такой системы может служить грузик на пружине.

Рассмотрим колебательную систему, состоящую из грузика массы m, подвешенного на невесомой пружине с коэффициентом упругости k. Можно показать, что сила тяжести для колебательного движения грузика существенной роли не играет. Уравнение второго закона Ньютона для грузика имеет вид:

(1.3)

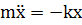
где x – смещение грузика относительно положения равновесия, -kx – сила упругости пружины. Применяя обозначение 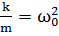, приведем это уравнение к виду:

(1.4)

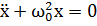
Здесь, как обычно при рассмотрении колебательного движения, точками над X обозначено дифференцирование по времени (т.е. 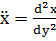). Нетрудно убедиться непосредственной подстановкой, что общее решение дифференциального уравнения (1.4) имеет вид:

(1.5)

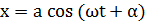
где а и α – некоторые постоянные, зависящие от начальных условий. Общее решение дифференциального уравнения (1.4) может быть представлено также в виде:

(1.6)

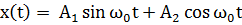
где A₁ и A₂ постоянные, также определяемые из начальных условий. Нетрудно показать, что эти два представленных решения дифференциального уравнения (1.4) эквивалентны.

В качестве другого примера системы, которая может совершать гармонические колебания, можно взять сплошной однородный диск, подвешенный на невесомой упругой проволоке (рис. 1.3). Смещение диска относительно положения равновесия описывается угловой координатой φ. Для описания динамики движения диска вокруг вертикальной оси естественно взять закон динамики вращательного движения:

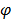Рис. 1.3

(1.7)

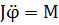
где J - момент инерции диска относительно вертикальной оси, проходящей через центр масс, М - момент силы, действующей на диск со стороны упругого подвеса. Согласно закону Гука M=-φD. Тогда уравнение динамики вращательного движения можно привести

(1.8)

к виду:

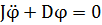
или

(1.9)

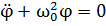
где 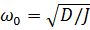- циклическая частота колебаний. Решением этого дифференциального уравнения является функция

(1.10)

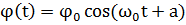
Таким образом, если диск выведен из положения равновесия и представлен самому себе, он будет совершать крутильные колебания по гармоническому закону с периодом

(1.11)

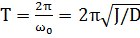
где D - постоянная, зависящая от упругих свойств, длины и поперечного сечения подвеса.

Анализируя эти два примера, можно установить следующие фундаментальные закономерности. Если закон динамики какой-либо системы преобразовывается в дифференциальное уравнение вида (1.4) или (1.9), то движение в системе совершается в виде гармонических колебаний. Сама система в этом случае называется гармоническим осциллятором, а дифференциальное уравнение — уравнением гармонического осциллятора. Его решением является уравнение гармонических колебаний.

Также одной из важнейших физических величин является энергия. Если материальная точка m совершает гармоническое колебательное движение по закону (1.5), то ее кинетическая энергия определяется формулой

(1.12)

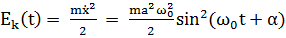
Потенциальная энергия определяется формулой

(1.13)

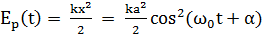
учитывая, что 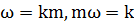, замечаем, что амплитуды E₁ и Е₂ -одинаковы:

(1.14)

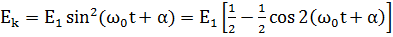
(1.15)

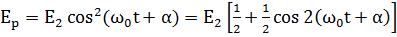
Рис. 1.4

На рис. 1.4 показана зависимость смещения x от t и соответствующие этому смещению

кинетическая и потенциальная энергии. Нетрудно убедиться, что полная энергия при этом остается постоянной.

2. ФИЗИЧЕСКИЙ И МАТЕМАТИЧЕСКИЙ МАЯТНИКИ

Физическим маятником называется твердое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси. Точка пересечения оси "О" с вертикальной плоскостью, проходящей через центр масс "А" тела, называется точкой подвеса маятника. Положение тела в каждый момент t можно охарактеризовать углом отклонения его из положения равновесия φ. Вращение тела происходит под действием силы тяжести, момент силы М для нее равен: 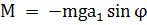, где a₁ - расстояние от оси вращения до Центра масс тела. Уравнение динамики вращательного движения для физического маятника записывается в виде:

(2.1)

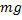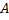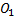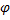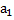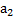Рис. 2.1

где J₁ - момент инерции тела относительно оси вращения, проходящего через точку подвеса маятника.

При малых колебаниях маятника 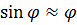, и уравнение (2.1) преобразуется к виду:

(2.2)

(2.2)

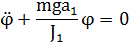
Полученное уравнение является дифференциальным уравнением второго порядка с постоянным коэффициентом перед φ. Обозначив его за 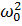приходим к широко известному уравнению гармонических колебаний.

(2.3)

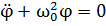
(2.4)

Подстановкой легко убедиться, что решением этого уравнения является функция

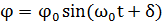
Данное соотношение аналитически описывает гармонические колебания, которые совершает физический маятник без учета сил сопротивления среды. Величина φ₀ определяет максимальное отклонение колеблющегося тела от положения равновесия и называется амплитудой колебания. Величина ω называется циклической частотой. Величину 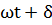называют фазой колебания, а ее значение при t=0, т.е. величину 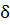- начальной фазой. Начальная фаза определяется положением тела, в котором оно находилось в момент начала отсчета времени. Если при t=O, φ=0; то 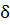=0 и 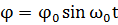. Если же при t=O, φ=φ₀; то 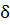=π/2 и .

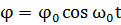Периодом гармонического колебательного движения называется наименьшее время Т, по истечении которого все величины, характеризующие это движение принимают первоначальное значение. Учитывая, что период синусоидальной функции равен 2л, из (2.4) следует, что за время Т фаза колебаний должна измениться на 2π. Т.е.

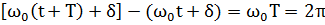
(2.5)

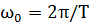
Поскольку за 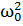мы обозначили величину 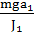, то период колебаний физического маятника

(2.6)

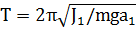
Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника, с амплитудой порядка нескольких угловых градусов изохронны.

МАТЕМАТИЧЕСКИЙ МАЯТНИК

(2.7)

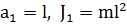Математический маятник является частным случаем физического маятника. Так называется маятник, вся масса которого практически сосредоточена в одной Точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника , где l - длина маятника и формула (2.6) переходит в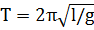

Сравнивая формулы (2.6) и (2.7) заключаем, что физический маятник колеблется так же, как математический с длиной

(2.8)

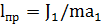
которая называется приведенной длиной физического маятника

(2.9)

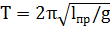
ОБОРОТНЫЙ ФИЗИЧЕСКИЙ МАЯТНИК

Приведенная длина физического маятника легко находится для так называемого оборотного маятника. Отложим от точки подвеса "О" вдоль прямой OA отрезок ОАО₁, длина которого равна приведенной длине физического маятника. Точка "O₁" называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.

Покажем, что действительно, если Найдены точки "О" и "O₁" лежащие на одной прямой с точкой центра масс "А" и находящиеся по разные стороны от точки "А", то расстояние OO₁ равно 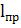, приведенной длине физического маятника, если периоды колебания его относительно осей вращения, проходящих через точки O и O₁, окажутся одинаковыми.

При колебании маятника относительно оси "О" согласно (2.6)

(2.10)

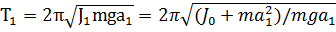
а относительно оси "O₁"

(2.11)

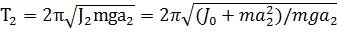
где J₀ - момент инерции тела относительно оси, проходящей через центр масс.

Возводим уравнение (2Л0) и (2.11) в квадрат и приводим к общему знаменателю, полагая T₁=T₂

(2.12)

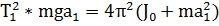
(2.13)

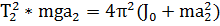
Вычитая из первого уравнения второе, получаем

(2.14)

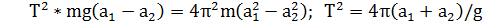
Сопоставляем (2.14) и (2,9) видим, что 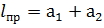, что и требовалось доказать.

3. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

В любой реальной колебательной системе всегда имеются силы трения, действие которых приводит к уменьшению энергии системы. Рассмотрим движение такой колебательной системы, которая была выведена внешними силами из состояния равновесия и предоставлена самой себе. Такие колебания называются свободными (или собственными). Ограничимся рассмотрением малых колебаний тела. Будем считать, что сила трения пропорциональна величине скорости 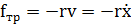, где r - коэффициент зрения. С учетом силы трения уравнение второго закона Ньютона имеет вид:

(3.1)

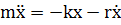
(3.2)

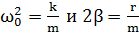Используя обозначения , перепишем его следующим образом: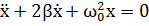

Если сила трения существенно меньше силы упругости, то колебания в такой системе можно описать функцией

(3.3)

Затухающие колебания совершаются с частотой 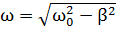, отличающейся от частоты ω₀, которую называют собственной частотой колебательной системы. График функции (3.3) дан на рис.3.1.

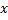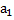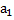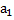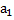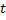Рис. 3.1

Движение такой колебательной системы можно условно рассматривать как гармоническое колебание с частотой ω и амплитудой a, зависящей от времени по закону:

(3.4)

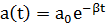
Скорость затухания "колебаний определяется величиной 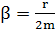, которую называют коэффициентом затухания. Величина 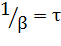дает время, за которое амплитуда колебаний уменьшается в e раз.

Количественно скорость затухания описывается отношением максимальных Отклонений в одну и ту же сторону:

(3.5)

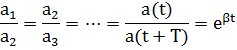
Это отношение называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:

(3.6)

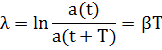
Степень затухания колебаний можно описать также числом колебаний N_e, совершаемых системой за время, когда амплитуда уменьшается в е раз. Его можно найти как отношение τ/T. Для характеристики колебательной системы часто используется величина

(3.7)

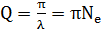
называемая добротностью колебательной системы.

4. НАКЛОННЫЙ МАЯТНИК

В предыдущем разделе рассмотрены затухающие колебания при наличии сил вязкого трения в системе. Существует и другой вид сил трения - это силы между поверхностями двух соприкасающихся твердых тел при отсутствии между ними жидкой или газообразной прослойки. Такие силы называют силами сухого трения. В зависимости от характера движения соприкасающихся тел друг относительно друга различают трение скольжения и трение качения.

Сухое трение возникает не только при скольжении одного тела по поверхности другого, но при всякой попытке вызвать такое скольжение.

В этом случае трение называют трением покоя или сцепления. При наличии сухого трения тело может находиться в состоянии покоя, даже если на него действует сила f , не превышающая максимального значения силы трения покоя f_тр. Наличие силы трения покоя - характерная особенность сухого трения, которое не исчезает при обращении в нуль относительных скоростей соприкасающихся поверхностей, в противном случае трение является жидким.

Как экспериментально установил Кулон (1736-1806), величина силы трения скольжения не зависит от величины площади соприкосновения твердых тел и пропорциональна силе нормального давления N, с которой одно тело действует на другое:

(4.1)

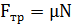
где постоянная 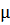называется коэффициентом трения скольжения. Наличие сухого трения приводит к износу деталей машин, с ним приходится бороться.

Наиболее радикальным способом уменьшения сил трения является замена трения скольжения трением качения (шарикоподшипники). Под трением качения понимают трение, возникшее, например, между шарообразным или цилиндрическим телом, катящимся без скольжения по плоской или изогнутой поверхности. Трение качения формально подчиняется тем же законам, что и трение скольжения. Силы сухого и вязкого трения относятся к диссипативным силам, т.е. к силам, при действии которых полная механическая энергия системы убывает, переходя в другие, немеханические формы энергии, например, в теплоту.

Рассмотрим, как можно оценить количественно диссипацию (рассеяние) механической энергии колеблющегося твердого тела при наличии сухого трения, трения скольжения и качения, с помощью наклонного маятника. Наклонный маятник представляет собой цилиндр или шар, подвешенный на нити, плоскость колебания которого может меняться. Обозначим угол, между плоскостями колебаний и вертикалью за 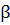. В таком случае сила нормального давления шара или цилиндра на плоскость, по которой катится или скользит, будет равна

(4.2)

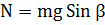
где m - масса маятника На основами (4.1) имеем

(4.3)

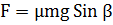
т.е. меняя угол 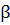можно менять и силу трения. В зависимости от характера движения грузика по опорной плоской поверхности твердой пластины - качение или скольжение - силы трения, действующие на грузик, будут существенно отличаться. При качении силы трения малы и маятник будет совершать затухающие колебания. При скольжении грузика по опорной плоскости силы трения существенно возрастают, и движение из Колебательного может превратиться в апериодический процесс. Рассмотрим движение маятника при скольжении цилиндрического грузика по опорной плоскости.

Закон сохранения энергии с учетом диссипативных сил трения при колебании маятника запишется в виде:

(4.4)

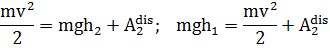
где 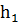- начальная высота грузика (рис. 4.1), 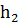- максимальная высота, на которую поднимется грузик через Т/2. Значение 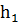и 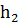можно выразить через длину маятника l и угол отклонения 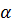от положения равновесия.

(4.5)

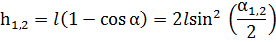
Из соотношения (4.4) работа диссипативных сил равна

(4.6)

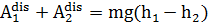
При малых углах отклонения маятника можно считать, что

(4.7)

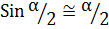
С другой стороны работу сил трения можно найти как произведение силы трения на длину пути, пройденного телом:

(4.8)

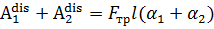
С учетом формул 4.3, 4.6, 4.7, 4.8 получаем выражение для экспериментального значения коэффициента трения скольжения

(4.9)

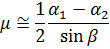
Используя те же самые экспериментальные данные можно оценить степень диссипации механической энергии маятника за счет сил трения скольжения. Коэффициент диссипации К можно представить таким образом:

(4.10)

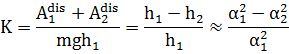
Увеличивая угол наклона оси маятника 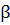, можно менять коэффициент диссипации K почти от 0 до 1. При некотором значении угла наклона 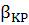смещенный относительно положения равновесия грузик уже не движется в сторону положения равновесия. Это означает, что возвращающая сила 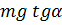стала равной силе трения покоя.

Рассмотрим характер движения маятника при качении шарика или цилиндра по опорной плоской поверхности. В этом случае грузик на нити совершает более сложное движение, которое можно рассматривать как вращательное движение вокруг собственной оси с угловой скоростью 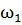и колебательное движение с угловой скоростью 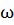относительно оси подвеса. Диссипация энергии в этом случае значительно меньше, силы трения сцепления вынуждают шарик или цилиндр катиться по плоской опорной поверхности. В процессе движения потенциальная энергия первоначального отклонения от положения равновесия тела переходит в кинетическую энергию движения грузика относительно оси подвеса и кинетическую энергию вращательного движения вокруг собственной оси.

Закон сохранения энергии для данного движения можно представить в виде

(4.11)

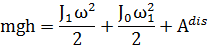
здесь mgh - потенциальная энергия отклоненного шарика. 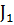-момент инерции шарика относительно оси подвеса, 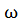- его угловая скорость вращения, 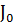и 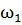- момент инерции и угловая скорость вращения шарика относительно собственной оси. Для шарика 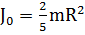для цилиндра, 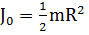, где R - радиус шарика или цилиндра. Если отсутствует проскальзывание при качении и выполняется условие 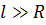, то 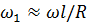, 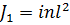Тогда закон сохранения энергии можно записать как

(4.12)

(4.13)

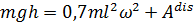для шарика

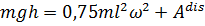для цилиндра

При вертикальном расположении плоскости качения маятника ( 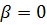) шарик или цилиндр не касаются твердой подложки. Пренебрегая силами сопротивления воздуха, колебания маятника можно считать собственными с частотой 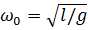Закон

(4.14)

сохранения энергии для вертикального маятника можно записать в виде

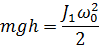
Учитывая соотношения 4.12, 4.13, 4.14 получаем:

(4.15)

(4.16)

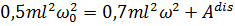для шарика

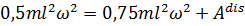для цилиндра

Степень диссипации механической энергии К для шарика можно представить как

(4.17)

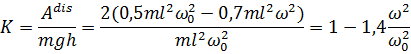
(4.18)

Аналогично для цилиндра

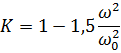
Или, выражая частоту колебаний через период по формуле 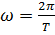, получаем

(4.19)

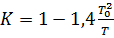для шарика

(4.20)

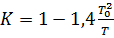для цилиндра

Степень диссипации энергии маятника будет сильно зависеть от угла наклона 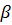, так как при изменении угла наклона существенно меняется сила нормального давления шара или цилиндра на опорную плоскость.

При малых 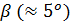вся работа сил трения качения идет на создание кинетической энергии 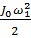, т.е. можно считать, что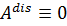

При малых :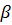

(4.21)

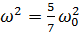или 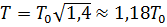для шара

(4.22)

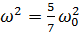и или 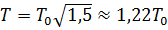для цилиндра

5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Одним из самых распространенных типов колебаний являются вынужденные колебания. Они наблюдаются как в механических колебательных системах, так и в электрических и находят широкое применение в технике. В некоторых случаях вынужденные колебания являются нежелательными и от них необходимо избавляться.

Вынужденными колебаниями называются такие колебания, которые возникают в колебательной системе под действием периодически изменяющейся силы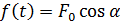

Рассмотрим движение грузика массы m на пружине с коэффициентом жесткости k. Уравнение движения можно записать в виде:

(5.1)

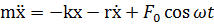
(5.2)

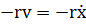где сила вязкого трения. Это уравнение можно привести к виду: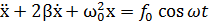

где введены следующие обозначения:

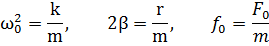
Уравнение (5.2) представляет собой неоднородное дифференциальное уравнение. Известно, что общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение:

(5.3)

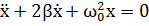
как известно, описывает затухающие колебания в системе и его решением является функция:

(5.4)

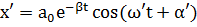
(5.5)

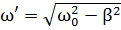где , а 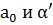– некоторые произвольные постоянные, зависящие от начальных условий. Надо найти частное (т. е. содержащее произвольных постоянных) решение неоднородного уравнения. Естественно предположить, что оно имеет вид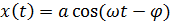

где а амплитуда вынужденных колебаний, 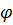сдвиг фаз между смещением грузика и вынуждающей силы. Дифференцируя функцию (5.5) один и два раза получим соответственно:

(5.6)

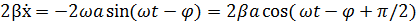
(5.7)

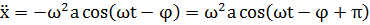
Третье слагаемое в левой части уравнения(5.2) имеет вид:

(5.8)

Таким образом, 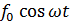является суммой трех колебаний той же частоты 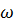, описываемых уравнениями (5.6), (5.7) и (5.8), причем колебание (5.6) смещено по фазе относительно (5.8) на 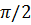, а (5.7) на .

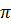Сложение трех гармонических колебаний (5.6), (5.7) и (5.8) можно выполнить методом векторных диаграмм.

Согласно этому методу колебание изображается в виде вращаю­щегося вектора, радиус которого равен амплитуд колебания , а угловая скорость — циклической частоте. Поскольку частоты всех трех колебаний одинаковы, во вращающейся системе отсчета эти колебания будут изображаться неподвижными векторами 1, 2, 3, которые соответствуют колебаниям (5.8), (5.6) и (5.7). В любой момент времен сумма лекторов 1, 2, и 3 должна быть равна вектору 4. Из векторной диаграммы находим, что это возможно при условии:

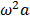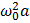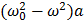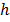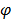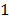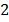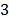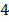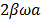Рис. 5.1

(5.9)

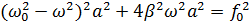
Отсюда можно найти амплитуду вынужденных колебаний

(5.10)

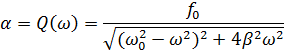
Из векторной диаграммы можно получить также соотношение

Таким образом, соотношение (5.10) и (5.11) полностью определяют частное решение (5.5) неоднородного дифференциального уравнения:

(5.11)

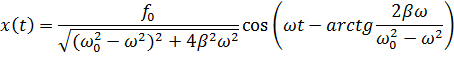
Общее решение неоднородного уравнения (5.2) имеет вид

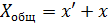
Собственные колебания в системе, описываемые слагаемым 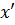, затухают со временем по экспоненциальному закону, так что слагаемое х' играет замытую роль лишь в начальной стадии процесса. На рис.52 представлен вид функции X(t).

Переходный режим

Рис. 5.2

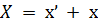
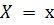
РЕЗОНАНСНЫЕ КРИВЫЕ

Зависимость амплитуды вынужденных копаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Для определения резонансной частоты необходимо найти максимум функции

(5.12)

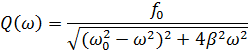
т.е. минимум функции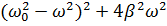

Продифференцируем по и приравняем к нулю:

(5.13)

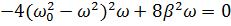
Уравнение (5.13) имеет три решения

(5.14)

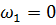
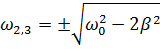
Первое решение соответствует максимуму знаменателя в формуле (5.13). Из двух других решений физический смысл имеет только положительное решение. Таким образом

(5.15)

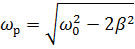
Зависимость (5.12) амплитуды вынужденных колебаний от частоты 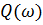изображена на рис.5.3, ее обычно называют амплитудной резонансной кривой. При малом коэффициенте

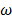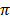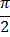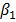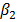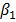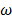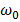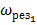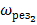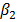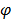Рис. 5.3

Рис. 5.4

(5.16)

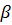затухания резонансная кривая имеет более острый максимум. При малом затухании 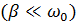амплитуда при резонансе будет равна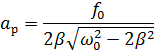

(5.17)

Разделим это выражение на смещение грузика постоянной силы

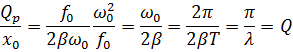
Где 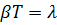— логарифмический декремент затухания. Таким образом, добротность колебательной системы Q можно определить как отношение амплитуды смещения при резонансе к смещению под действием постоянной силы.

Вынужденные колебания отстают по фазе от вынуждающей силы на 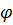, причем это смещение зависит от частоты и определяется формулой (5.11). График этого соотношения представлен на рис. 5.4 и называется фазовой резонансной кривой.

6. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

6.1. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ ОБОРОТНОГО И МАТЕМЕТИЧЕСКОГО МАЯТНИКОВ

Экспериментальное определение ускорения свободного падения осуществляется с помощью универсального маятника FRM - 04, общий вид которого показан на рис. 6.1.1. На вертикальной стойке основания 1 крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360°. С одной стороны кронштейна 2 подвешен математический маятник 3, а с другой - физический оборотный маятник 4. Физический оборотный маятник представляет собой стальной стержень 5 с двумя грузами 6, подвешенный на опорной призме. Стержень 5 имеет кольцевые проточки, нанесенные через 10 мм, которые служат для надежной фиксации грузов и опорных призм, а также для отсчета расстояниями между ними.

Фотоэлектрический датчик 7, позволяет измерить время выбранного экспериментатором числа колебаний с точностью до 0.001 сек. С этой целью датчик устанавливается на такой высоте, чтобы колеблющийся маятник при своем движении перекрывал луч света датчика. При нажатии кнопки "Пуск" начинается отсчет времени. Чтобы датчик зафиксировал время, соответствующее 10 колебаниям, необходимо нажать кнопку "Стоп" когда на цифровом индикаторе числа периодов появится цифра "9".

Использование математического и физического маятников основано на том, что период их колебаний при малой их амплитуде (6°— 8°) зависит только от длины маятника и ускорения свободного падения, поэтому можно с хорошей точностью находить значения ускорения свободного падения

(6.1.1)

Рис. 6.1.1

(6.1.2)

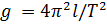— для случая математического маятника

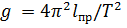— для физического маятника

где 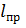— приведенная длина физического маятника.

Измерение и обработка результатов.

Для расчета ускорения свободного падения но формуле (6.1.2) необходимо найти приведенную длину физического маятника и соответствующий этому период колебаний. Для определения этих величин исследуется зависимость периода колебаний маятника в прямом (условно) и перевернутом на 180 градусов положении маятника при изменении положения подвижного груза 1 (см. рис. 6.1.2)

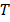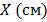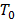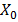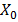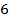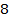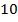Рис. 6.1.2

В начальное положении подвижный груз 1 располагается у опорной призмы 2. Маятник устанавливается в рабочее положение на установке и отклоняется на небольшой угол (5°— 8°). Отсчет числа колебаний n и времени, за которое эти колебания совершаются t начинают, пропустив 8 — 10 начальных колебаний. По измеренным величинам рассчитывается период колебаний 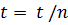. Затем маятник переворачивают на 180° и также измеряют период колебаний. После этого подвижный груз 1 устанавливается в новое положение и измерения повторяются. По полученным данным строится зависимость периода колебаний маятника в прямом и перевернутом положении от величины х. Находят точку пересечения двух линий на графике и соответствующий этой точке период 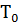. По формуле (6.1.2) рассчитывают ускорение свободного падения.

После экспериментов с оборотным маятником кронштейн 2 поворачивают и устанавливают в рабочее положение «математический маятник». Измерив длину маятника 1 и период колебаний Т, по формуле (6.1.1) рассчитывают ускорение свободного падения g.

Контрольные вопросы

1. Используя закон динамики вращательного движения получить уравнение гармонического осциллятора.

2. Получить формулу для периода колебаний математического маятника из формулы для периода колебаний физического маятника.

3. Как определяются направления векторов ( 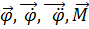, они взаимосвязаны?

4. Что такое приведенная длина физического маятника?

6.2 ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Для исследования затухающих колебаний используется установка универсальный маятник FPM-04 с несколько измененной конструкцией физического маятника. Общий вид универсального маятника показан на рис. 6.2.1

Основание 1 оснащено регулируемыми норками, которые позволяют устанавливать основание в горизонтальном положении. В основании установки закреплена вертикальная стойка 2, на которой укреплены верхний кронштейн 3 и нижний кронштейн 4 с фотоэлектрическим датчиком 5.

Рис. 6.2.1

Физический маятник выполнен в виде стального стержня 6, на котором укреплены опорная призма 7, дополнительный груз 8 и пластинка из дюралюминия 9 для увеличения сил сопротивления, т.е. для получения быстро затухающих колебаний. С помощью шкалы 10 можно определять смещения маятника последовательно через каждый период 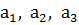и т.д. и по ним рассчитать декремент, а за ним логарифмический декремент.

Сигнал с фотоэлектрического датчика 5 поступает на миллисекундомер 11, который позволяет измерять число колебаний n (число периодов) и полное время t. По этим данным можно рассчитать период колебаний (Т = t / n).

Измерение и обработка результатов.

Перед началом работы необходимо проверить: правильно ли установлена опорная призма на верхнем кронштейне, совпадает ли положение указателя смещений с нулевой отметкой шкалы. Затем маятник отклоняют до максимального положения по шкале 10 и отпускают. Маятник будет совершать затухающие колебания, в процессе которых необходимо измерять максимальные значения последовательных отклонений в одну и ту же сторону 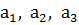и т.д. По которым рассчитывается декремент затухания:

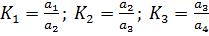и т. д.