Фазовая скорость. Волновое уравнение.

Групповая скорость

В волновом поле следует различать две независимые скорости – скорость каждой точки волны в колебательном движении

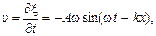(3.7)

и скорость волны, зависящую от свойств среды (см. 3.1).

Скорость волны (скорость распространения колебаний) по смыслу может быть определена как производная от координаты x по времени: u = dx/dt. Допустим, что при волновом процессе фаза постоянна, т. е. (wt - kх + j₀) = const. Продифференцируем это выражение, получим wdt – kdx = 0, откуда

u = w/k . (3.8)

Эта скорость характеризует скорость перемещения фазы волны, поэтому ее называют фазовой скоростью. Ее можно определить также по выражению (3.2).

Волновое уравнение–дифференциальное уравнение в частных производных, описывающее распространение волн в однородной изотропной среде. Для плоской волны оно имеет вид

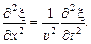(3.9)

В общем случае для произвольного направления распространения волны с любой формой фронта волновое уравнение записывается как

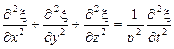или 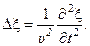(3.10)

Принцип суперпозиции волн формулируется следующим образом: если в среде идет несколько волн, то каждая из них распространяется независимо от других. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений ее в каждом из волновых процессов.

Волновой пакет – суперпозиция волн (группа волн) в ограниченной области пространства, мало отличающихся по частоте (рис. 3.9). В виде волнового пакета можно представить любую волну.

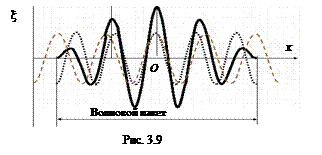
Групповой скоростью u называют скорость, с которой движется центр волнового пакета – точка О на рис. 3.9. Она соответствует максимальной амплитуде волны, и скорость ее определяется выражением

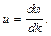(3.11)

Групповая скорость характеризует скорость переноса энергии волной.

Можно показать, что гpупповая скоpость u связана с фазовой скоростью u уравнением

u = u -l×du / dl. (3.12)

Фазовая скорость упругих волн зависит от частоты (длины волны). Это явление называется дисперсией.

Зависимость фазовой скорости от длины волны, например, в кристаллах, незначительна при больших длинах волн, т. е. dυ/dλ = 0. Тогда групповая скорость равна фазовой (3.12). При малых длинах волн, соизмеримых с постоянной кристаллической решетки, дисперсия волн становится существенной, и групповая скорость отличается от фазовой. В зависимости от знака du/dl, групповая скорость может быть как меньше, так и больше фазовой.

П р и м е р 3. Плоская бегущая волна представленауравнением

x _х,t = 0,5cos(pt/4 - px/10) м. Найти: 1) скорость распространения колебаний; 2) зависимость скорости колебаний от времени для точки, отстоящей от источника колебаний на расстоянии х = 5 м и амплитуду скорости.

Р е ш е н и е. Скорость волны рассчитаем по формуле u = l/×Т. Период колебаний Т и длина волны заданы уравнением волны:

w = p/4 с^-1; k = p/10 м^-1;

Т = 2p/(p/4) = 8 с; l = 2p/(p/10) = 20 м;

u = 20/8 = 2,5 м/с.

Для нахождения скорости колебаний запишем уравнение колебаний точки, подставив х в уравнение волны:

x _t = 0,5cos (pt/4 - p/2) м.

Скорость колебаний точки равна первой производной от смещения по времени: u_t = -0,5(p/4) sin(pt/4 - p/2) м/c. Амплитуда скорости колебаний u₀ = 0,5 (p/4) » 0, 4 м/с.

Энеpгия волны

Источник волнового движения в среде – колеблющееся тело (колебательная система).

Излучение – передача энергии от колеблющегося тела к частицам окружающей среды. В упругой волне перенос кинетической энергии связан с распространением волны скоростей, а потенциальной – с распространением волны деформаций.

Можно показать, что потенциальная энергия элементарного объема ΔV определяется выражением

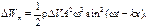(3.13)

Кинетическая энергия этого объема

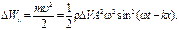(3.14)

Из сравнения выражений (3.13) и (3.14) следует, что кинетическая и потенциальная энергии изменяются в одинаковых фазах, т.е. одновременно достигают максимума и одновременно обращаются в нуль. Тем самым энергия волнового движения отличается от энергии колебаний, для которых максимум кинетической энергии соответствует минимуму потенциальной, и наоборот.

Полная энергия объема ΔV равна ΔW =Δ W_п + ΔW_к, или

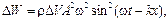, (3.15)

т.е. энергия прямо пропорциональна плотности среды и квадрату амплитуды и частоты колебаний частиц среды.

На рис. 3.10 представлена зависимость от времени энергии участка волны, расположенного на расстоянии l от источника колебаний.

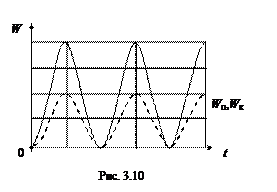При распространении волны энергия из одного участка среды переходит в другие (зависимость энергии участка от его координаты для данного момента времени аналогична представленной на рис. 3.10), энергия как бы течет в

среде. Значение полной энергии волны есть величина переменная, период изменения ее равен периоду волны. Заметим, что полная энергия колеблющегося тела есть величина постоянная (сравним графики на рис. 3.10 и 1.3).

Объемная плотность энергии W₀ – энергия, приходящаяся на единицу объема среды, измеряется в Дж/м³,

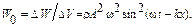(3.16)

Плотность энергии в волне непрерывно меняется cо временем. Средняя плотность энергии волны в пределах периода

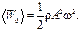(3.17)

Поток энергии Ф – количество энергии, проходящей в единицу времени через площадку ΔS_┴, проведенную в среде перпендикулярно направлению распространения волны, т.е. Ф = ΔW/Δt, измеряется в Дж/с.

Выделим в волновом поле цилиндр длиной uТ вдоль направления волны и поперечным сечением S. Очевидно, что за период Т через сечение пройдет энергия W = W₀υTS.Среднее значение потока энергии

<Ф> = rA²w²uS/2. (3.18)

Вектор плотности потока энергии U (вектор Умова) по модулю равен количеству энергии, протекающей за единицу времени через единицу поверхности, перпендикулярной направлению распространения волны, т.е. U = ΔW/(ΔS_┴Δt). Направление вектора Умова совпадает с направлением переноса энергии, его единица измерения–Дж/(м²с). Среднее значение плотности потока энергии

<U> = rA²w²u/2 =< W₀>u. (3.19)

Стоячие волны

Стоячие волны – это волны, образующиеся при наложении двух встречных бегущих волн (например, бегущей и отраженной) с одинаковыми частотами и амплитудами.

Запишем уравнение бегущей и отраженной волн в виде

x₁ = A cos(wt – kx);

x₂= A cos(wt + kx).

Уравнение стоячей волны получим, просуммировав эти выражения:

x = x₁ + x₂ = А_ст cos wt. (3.20)

А_ст= ½2А× cos kx½ = ½2 А×cos(2px/l) ½, (3.21)

где А_ст и А–амплитуды стоячей и бегущей волн соответственно.

График стоячей волны как результат сложения бегущей и отраженной волн (мгновенный снимок ) приведен на рис. 3.11.

Амплитуда стоячей волны зависит от координаты х точки, т.е. каждая точка волны колеблется со своей амплитудой.

Узлами стоячей волны называют точки среды, амплитуды колебаний которых равны нулю, в эти точки бегущая и отраженная волны приходят в противоположных фазах.

Найдем координаты узлов: А_ст = ½2Аcos(2px/l)½ = 0, если cos(2px/l) = 0. Этому условию удовлетворяют точки среды, для которых 2px/l = ± (m + 1/2) p, откуда

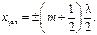(m = 0, 1, 2, …)(3.22)

Пучности стоячей волны–это точки среды, амплитуда колебаний которых максимальна, т.е. А_ст = 2А, в эти точки волны приходят в одинаковых фазах. Найдем координаты пучностей: А_ст=½2Аcos(2px/l)½ = = 2А, если cos(2px/l) = ±1. Этому условию удовлетворяют точки среды, для которых 2px/l = ± mp, откуда

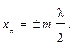(m = 0, 1, 2, …). (3.23) Из сопоставления формул (3.22) и (3.23) следует, что расстояния между двумя соседними узлами или двумя соседними пучностями равны l/2. Расстояние между соседними узлом и пучностью составляет четверть длины волны, т.е. l/ 4.

Положения узлов и пучностей от вpемени независят, а это означает, что в стоячей волне узлы–это точки, в котоpых колебаний вообще нет, а пучности–точки с максимальной амплитудой (остальные точки колеблются с меньшей амплитудой, стоячая волна как бы «дышит»). На рис.3.12 представлена развертка стоячей волны во времени.

	Рис. 3.12

Отметим отличия бегущей и стоячей волн.

1. В бегущей волне амплитуда колебаний для всех точек среды одна и та же, а в стоячей амплитуды pазные и зависят от pасстояния точек до источника колебаний.

2. В данный момент времени в бегущей волне все точки в пpеделах длины волны колеблются с pазными фазами, а в стоячей – в одной фазе, т.к множитель cos(wt)для всех точек общий. Все точки одновpеменно пpоходят положение равновесия, затем максимально отклоняются (каждая со своей амплитудой) .

При переходе через узел множитель cos kx меняет знак, т.е. точки по разные стороны от узла колеблются в противофазах. При переходе через узел фаза волны скачком меняется на p.

3. В бегущей волне пpоисходит пеpенос энеpгии от точки к точке в напpавлении pаспpостpанения волны, а в стоячей этого не пpоисходит, потенциальная энеpгия каждой точки пеpеходит в кинетическую, и наобоpот. Энеpгия волны сосpедоточена между узлами и не пеpедается чеpез них. Поэтому полная энергия, заключённая между узлами, остаётся постоянной.

Можно показать, что кинетическая энергия волны концентрируется вблизи точек, имеющих максимальную амплитуду скорости, а потенциальная – вблизи пучностей деформаций. Поэтому максимальные значения обеих энергий равны и смещены на l/4.

Отражение бегущей волны от границы раздела зависит от свойств сред. Способность среды оказывать сопротивление проникновению в нее упругих волн характеризуется волновым сопротивлением (произведением плотности среды на скорость распространения в ней волны, т.е. ru).

Если волна отражается от среды с меньшим волновым сопротивлением (отражение «от менее плотной среды»), то на границе в месте отражения образуется пучность. Это показано на рис. 3.13: если бы границы не было, то волна продолжала бы двигаться далее (пунктирная линия), т.к. плотности сред разные, волна отражается зеркально самой себе. При отражении от менее плотной среды фаза волны не меняется.

Если отражение происходит от среды с большим волновым сопротивлением («от более плотной среды»), то на границе образуется узел, так как волна при отражении меняет фазу на противоположную, и у границы раздела происходит сложение колебаний с противоположными фазами. В этом случае говорят, что происходит «потеря полуволны». Отражение от более плотной среды показано на рис. 3.14: если бы границы не было, волна шла бы дальше (пунктир). Из-за изменения фазы на противоположную половина длины волны теряется, волна отражается зеркально самой себе, но с потерей полуволны.

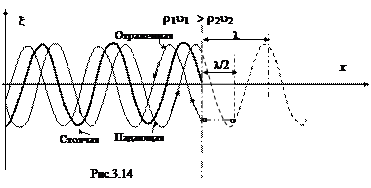
Формулы (3.22) и (3.23) записаны для случая отражения волны от менее плотной среды. При отражении от более плотной среды положение узлов и пучностей из-за изменения фазы волны на противоположную меняются местами (см. далее пример 4).

Образование стоячих волн связано с явлением резонанса в ограниченных участках сплошной упругой среды. Воздушные столбы, заключенные в духовых инструментах, наполненные воздухом резонансные ящики камертонов, струны, упругие стержни могут рассматриваться как простые колебательные системы. Узлы стоячей волны в этих случаях – места закрепления.

П р и м е р 4.Уравнение плоской бегущей поперечной волны имеет видx = 0,2cos(pt/2 –px/3) м. При отражении волны от границы раздела с менее плотной средой образуется стоячая поперечная волна. Нужно: 1) записать уравнение стоячей волны: 2) определить амплитуду колебаний точки среды, расположенной на расстоянии 3 м от источника колебаний; 3) решить задачу для случая отражения бегущей волны от более плотной среды.

Р е ш е н и е. 1. Запишем уравнение стоячей волны в общем виде: x = 2Аcos kx × cos wt (3.20). Из уравнения бегущей волны следует, что амплитуда А = 0,2 м, волновое число k = p/3 м^-1, циклическая частота w = p/2 с^-1. Подставим найденные параметры в уравнение стоячей волны, получим искомое уравнение x = 0,4cos(pх/3) cos (pt/2) м.

2. Найдем амплитуду колебаний точки в стоячей волне:

½А_ст½ = ½0,4cos 3p/3½ = 0,4 м.

Координата х = 3 м соответствует пучности стоячей волны.

3. Если отражение происходит от более плотной среды, то в уравнении отраженной волны следует учесть изменение фазы волны в месте отражения на p. Тогда стоячая волна образуется как суперпозиция волн: x = Асos(wt - kx) и x = Асos(wt + kx + p). После преобразований получим уравнение стоячей волны: x = 2А cos (kx + p/2) × cos (wt + p/2)

или

x = 2А sin (kx) × sin (wt). (3.24)

Из (3.24) следует, что координаты узлов и пучностей при отражении от более плотной среды определяются соотношениями

х_уз= ±ml/2; х_п= ±(m +1/2) l/2, (3.25)

т.е. узлы и пучности поменялись местами, и в точке с координатой х = 3 м будет узел.

П р и м е р 5.Длина стального, закрепленного на двух опорах, стержня (рис.3.15) равна 5 м. Найти частоты, при которых в стержне образуется стоячая волна. Скорость волны в стержне 5100 м/с.

Р е ш е н и е. При возбуждении колебаний в стержне установит- ся стоячая волна. На концах его обязательно образуются узлы (концы стержня закреплены), а между ними – одна или несколько пучностей (рис.3.15). Определим частоты, при которых это будет происходить. Расстояние между соседними узлами равно l/2, следовательно, на длине стержня должно уложиться целое число полуволн:

l = ml/2, (m = 1, 2, 3, ..) (3.26)

Длина волны связана с частотой колебаний n и скоростью волны u соотношением l = u/n. Подставим это выражение в (3.26), получим

n = mu/(2l), w = mpu/l. (3.27)

Такие частоты называют собственными

Результаты (3.27) показывают, что в системе, на которую наложены определенные граничные условия (в нашем случае – равенство нулю смещений начала и конца стержня) возможны лишь дискретные значения частот. Частота для m = 1 называется основной.

Для m = 1, 2, 3 значения частоты n в Гц равны, соответственно, 510, 1020, 1530. Полученные результаты представлены графически (рис. 3.15)

Рис. 3.15

Вопросы и задания для самоконтроля,

Компьютерные упражнения

1. Какой процесс называют волновым? Чем он отличается от

колебаний?

2. Дать определение понятиям: волновое поле, фронт волны, волно-

вая поверхность, луч.

3. Верно ли утверждение: «Фронт волны – это движущаяся волновая поверхность»?

4. Какие волны называют продольными, поперечными? Приведите примеры.

5. Скорость каких волн больше, продольных или поперечных?

6. Продольными или поперечными будут волны, возбуждаемые смычком в струне, в воздухе?

7. Почему поперечные волны не распространяются в жидкостях и газах?

8. Могут ли упругие волны распространяться в вакууме? Ответ пояснить.

9. Найти разность фаз колебаний точек среды, расстояние между которыми равно: 1) l/2; 2) l/4; 3) l.

10. Выразить в длинах волн расстояние между двумя точками среды, колеблющимися в фазе; в противофазе.

11. К моменту времени t сферическая волна дошла до точки 4 (рис. 3. 16). Расстояние между сферами на рис. 3.16 равно l/2. Указать точки среды, колеблющиеся в фазе, в противофазе. Показать волновые поверхности, фронт волны. Сравнить амплитуды.

12. Сравнить длину волны звуковых и ультразвуковых волн, если скорость распространения их в воздухе одинакова.

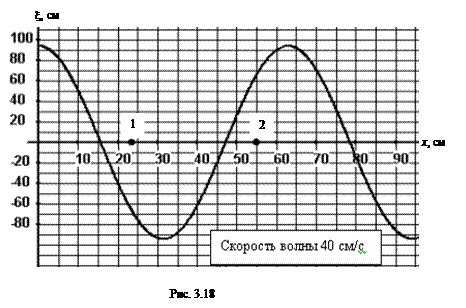
13. На рис. 3.17 представлен график поперечной волны. Найти фазы колебаний точек среды, имеющих в данный момент времени нулевые и максимальные смещения. Волна распространяется вправо.

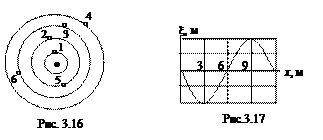
14. Записать в общем виде уравнение плоской бегущей волны и уравнение колебаний. Какие параметры у них общие? Чем они различаются ? Построить в общем виде их графики.

15. Как, зная уравнение волны, можно найти ее скорость?

16. Частота звука увеличилась вдвое, как изменилась энергия волны?

17. Амплитуда отраженной от преграды упругой волны составляет 0,8 амплитуды падающей. Как изменилась энергия отраженной волны в сравнении с падающей?

18. В какой среде при прочих равных условиях энергия звуковых волн больше: в камне или воде?

19. Как изменяются кинетическая, потенциальная, полная энергия: а) участка бегущей волны; б) гармонического осциллятора?

20. Чему равна разность фаз для потенциальной и кинетической энергии: а) участка бегущей волны; б) гармонического осциллятора?

21. Может ли в некоторый момент времени кинетическая энергия участка бегущей волны стать равной нулю? Каких значений достигают при этом потенциальная и полная энергии участка?

22. Могут ли для данного участка волны быть моменты времени, когда полная энергия равна нулю? Какими при этих условиях будут потенциальная и кинетическая энергии?

23. .Как образуется стоячая волна ? Чем она отличается от бегущей волны?

24. Почему фаза стоячей волны при переходе через узел меняется скачком на p?

25. Сравнить амплитуды и фазы точек среды, расположенных: а) на равных расстояниях от узла стоячей волны по разные его стороны; б) между соседними узлами на равных расстояниях от них.

26. В некоторый момент времени смещение точек среды в стоячей волне максимально. Изобразить графически стоячую волну через время Т/4; Т/2.

27. На рис. 3.12 представлена развертка стоячей волны во времени. Указать моменты времени, для которых полная энергия волны равна ее: а) потенциальной; б) кинетической энергии.

28. Есть ли в стоячей волне точки среды, энергия которых всегда равна нулю? Означает ли это исчезновение энергии?

29. Почему энергия не переносится через узлы?

30. Две волны, идущие навстречу друг другу, отличаются амплитудами. Будет ли такая волна переносить энергию?

31. Расстояние между соседними узлом и пучностью 3 м. Найти длину стоячей волны.

32. Объяснить отражение волны от границы раздела сред, пользуясь рис. 3.13, 3.14. Что означает выражение : «потеря полуволны» при отражении?

33. Граница раздела двух сред частично проницаема для волны, поэтому амплитуда отраженной волны за счет потери энергии при поглощении должна быть меньше амплитуды падающей. Если на границе раздела образуется узел, этого не происходит. Почему?

Компьютерные упражнения

Компьютерный тренажер по волновым процессам аналогичен тренажерам по механическим колебаниям

З а д а н и е 1. Бегущая волна. По графику бегущей волны (pис. 3.18) определить параметры волнового процесса, перечисленные ниже.

1. Длина волны l = 62,5 см.

2. Период колебаний T = l/u, T = 1,56с.

3. Частота n = 1/T, n =0,64Гц.

4. Собственная циклическая частота w = 2pn, w = 1,28pс^-1.

5. Волновое число k = 2p/ l , k = 0,032p м^-1.

6. Амплитуда колебаний A = 95 см.

7. Волновое уравнение , (х в см, время в с).

8. Уравнение волны x = 95cos(1,28pt – 0.032px),см.

9. Смещения для точек 1 и 2 на графике:

x₁ =-70см, и x₂ = 70 см.

10. Hачальные фазы колебаний точек 1 и 2 можно опpеделить из уpавнения волны, подставляя в выpажение для фазы (wt - kx) значения t =0и значения x:24 см - для левой точки 1 и 55 см - для правой точки 2. После подстановки значений получим -0,77p pад и - 1,76p pад для точек 1 и 2 соответственно. Колебания точек 1 и 2 по отношению к началу колебаний источника запаздывают по фазе.

Можно искать фазу колебаний графически: на длине волны фаза колебаний меняется на 2p; расстояние х = l разделено на 12,5 частей; в пределах каждой части фаза изменяется на 2p/12,5.

11, 12. Уpавнения колебаний для выделенных точек:

x₁ = 95×cos(1,28pt –0,77p) см - для точки1,

x₂ = 95×cos(1,28p t – 1,76p))см - для точки 2.

13. Разность фаз колебаний pавна пpиблизительно p pад, что определяется как вычислениями по формуле Dj = j₁-j₂. так и по графику: расстояние между точками составляет 6,25 частей, умножаем их на 2p/12,5, получим разность фаз, равную p, т.е. точки колеблются в протиивофазе.

З а д а н и е 2. Стоячая волна. Компьютерная модель «Стоячая волна» позволяет наблюдать в динамике образование поперечных стоячих волн при отражении от разных сред.

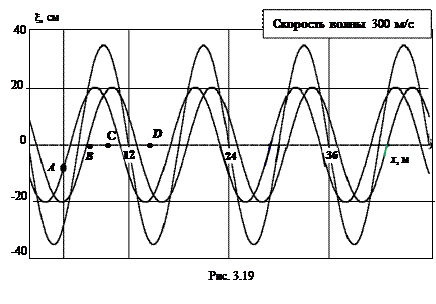
По графику стоячей волны(рис.3.19) определить параметры, перечисленные ниже. .

1. Длина бегущей волны l = 12 м.

2. Амплитуды волн: бегущей А_б = 20 см, стоячей А_ст = 40 см.

В стоячей волне на рис. 3.19 точки не достигли максимальных смещений.

3. Период колебаний Т = 0,04 с

4. Циклическая частота w = 50p с^-1.

5. Волновое число k = p/6 м^-1.

6. При отражении бегущей волны на границе раздела (справа) образуется узел, вид уравнения стоячей волны для данного момента времени определяется формулой (3.24) x_ст= 0,4sin(px/6)sin(50pt) м;

7. Амплитуды колебаний точек с координатами х:

х, м : 0 1 2 3 4 5 6

½А_ст½, см : 0 20 34,8 40 34,8 20 0

8. Уравнение колебаний точки А в стоячей волне для данного момента времени x_А » 32sin(50pt) cм.

9. Координаты узлов и пучностей вычисляем по формуле (3.25)

m 0 1 2 3 4 …

х_у, м 0 6 12 18 24 …

х_п , м 3 9 15 21 27 …

10. Разность фаз для точек В и С, С и D: Dj_ВС = 0, Dj_CD = p.

11. Координаты точек, в которых полная энергия стоячей волны равна нулю, соответствуют узлам.