Примеры задач. Измерь площадь большого треугольника, используя в качестве единицы измерения площадь маленького треугольника

Измерь площадь большого треугольника, используя в качестве единицы измерения площадь маленького треугольника. Запиши получившееся число.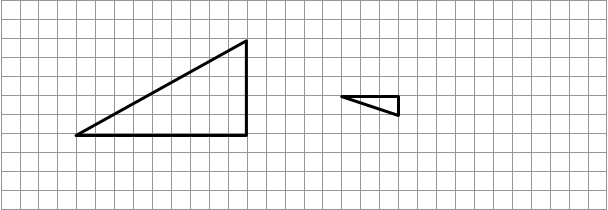

Ответ: 15

Необходимо реконструировать функциональное поле основного способа действия и убедиться в невозможности решить задачу как путем прямого укладывания мерки на объект, так и путем перекраивания формы фигуры или мерки при сохранении площади. Конструктивным выходом за границы обычного способа действия является достраивание измеряемой фигуры и единицы измерения до прямоугольников (т.е. удвоение площадей), основанное на понимании, что одновременное увеличение величины и мерки в одно и то же число раз сохраняет результат измерения.

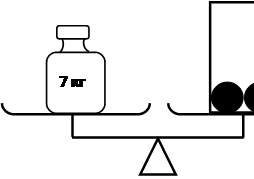
Имеются одинаковые чугунные ядра и ящик для их хранения. По результатам двух взвешиваний, которые показаны на рисунках 1 и 2, определи, сколько весит ящик с 6 ядрами.     Ответ__________________

Ответ: 17кг

В этой задаче в отличие от аналогичной задачи 2 уровня ни один рисунок по отдельности не позволяет найти необходимые данные для решения задачи (ни массу ядра, ни массу ящика). Необходим мысленный эксперимент с конструктивным преобразованием ситуации. Например, мысленно объединив грузы, находящиеся на левых чашках весов, в один груз, а на правых – в другой, получаем новую ситуацию равновесия, которая позволяет найти массу четырех ядер, а следовательно и массу любого числа ядер. После этого уже просто найти и массу пустого ящика, а, значит, и ящика с 6 ядрами.

Раздел 3. Зависимости

В рамках данного раздела индикаторами 3 уровня служат задачи, в которых решение не сводится к однозначной последовательности арифметических действий, а требует рассмотрения и опробования вариантов свете заданных условий и требований.