Запишите параметрические и канонические уравнения прямой в пространстве

1) Параметрическое уравнение прямой в пространстве:

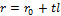
или

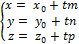
2) Каноническое уравнение прямой в пространстве:

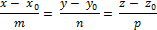
Запишите общее уравнение прямой в пространстве.

Прямая в пространстве получается за счёт пересечения двух плоскостей, поэтому её уравнения записывается в виде системы:

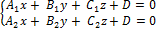
Опишите процесс перехода от общих уравнений прямых в пространстве к каноническим и параметрическим.

Для этого нужно найти любое решение системы, определив, таким образом, точку, принадлежащую прямой. Затем нужно найти векторное произведение нормальных векторов плоскостей, образующих прямую. После этого остаётся только записать каноническое уравнение прямой. Из канонического в параметрическое уравнение перейти очень легко.

Запишите в векторной форме формулу вычисления расстояния от точки до прямой в пространстве.

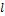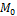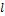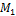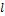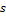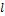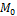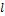Пусть – прямая в пространстве; – точка в пространстве, не лежащая на ; – точка на прямой ; – направляющий вектор прямой . Тогда расстояние от до будет вычисляться по следующей формуле:

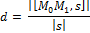
Запишите в векторной форме формулу для вычисления расстояния между двумя прямыми в пространстве.

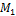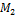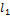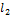Пусть и – произвольные точки на первой и второй прямой соответственно; и – направляющие векторы первой и второй прямой соответственно. Тогда формула нахождения расстояния между двумя скрещивающимися прямыми:

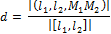
169. Как охарактеризовать взаимное расположение двух прямых в пространстве?

Пусть 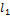и 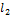– направляющие векторы первой и второй прямой соответственно.

1) Если скалярное произведение 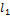и 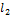равно нулю, то прямые коллинеарны.

2) Если скалярное произведение 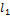и 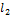отлично от нуля и расстояние между прямыми равно нулю, то прямые пересекаются.

3) Во всех остальных случаях прямые перекрещиваются.

Дайте определение эллипса.

Эллипс – множество всех точек плоскости, для которых сумма расстояний от двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Запишите каноническое уравнение эллипса. Объясните выбор декартовой системы координат. Изобразите эллипс на рисунке.

Каноническое уравнения эллипса:

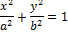
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться своим каноническим уравнением.

Дайте определение эксцентриситета эллипса и его директрис.

Эксцентриситет эллипса – это величина, меньшая единицы, вычисляемая по формуле:

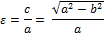
Директриса эллипса – прямая, существующая для каждого из фокусов, причём такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса.