Тема № 2. Ветер и его действие на здания и сооружения
Ветровое давление на сооружение – давление или разряжение, создающиеся на поверхности сооружения обтекающим его ветром.Как ветровой поток действует и на строительный объект, так и этот объект оказывает влияние на воздушный поток, деформируя его и изменяя характер течения.
В средней части России нагрузка от ветра (скоростной напор ветра) на высоте до 10 м принимается равным 270 Па, а на высоте 100 м она уже равна 570 Па. В некоторых районах береговой полосы Арктики и Приморья нормативное значение ветрового напора на высоте до 10 м равно 1 кПа.
С подветренной стороны здания возникает разряженное пространство, которое создает отрицательное давление – отсос, что увеличивает общее воздействие ветра. Сильные порывы ветра создают, кроме того, и ударное, динамическое воздействие на здание, еще более усложняя условия для расчета и проектирования конструкции.
Аэродинамический расчет и анализ высотных зданий и малоэтажных сооружений являются различными. Это связано с тем, что у высотных зданий наблюдается существенная разница давлений между основанием и крышей.
Знание геометрии потока вокруг здания необходимо при проектировании территории около здания, так как здесь могут возникать сильные потоки воздуха и вихри.
Аэродинамический анализ объектов позволяет разместить все здания наиболее выгодным образом по отношении друг к другу, выбрать форму сооружения, обеспечивая требуемый микроклимат в помещениях здания и в районе строительства в целом.
Основным инструментом исследования ветровых нагрузок является физический эксперимент в аэродинамических трубах. Но на предварительных этапах проектирования проводятся и численные расчеты (СНиП 2.01.07-85).
Ветровая нагрузка определяется как сумма средней и пульсационной составляющих.
Нормативное значение средней составляющей ветровой нагрузки wm (Па) над поверхностью земли определяется по формуле
wm=wokc,
где wo – нормативное значение ветрового давления, Па;
k – коэффициент, учитывающий изменение ветрового давления по высоте;
c – аэродинамический коэффициент.
Нормативное значение ветрового давления можно найти по формуле
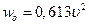 ,
,
где υ – скорость ветра, м/с.
Коэффициент k определяется по таблице 2.1 в зависимости от высоты здания и типа местности:
А – открытые побережья морей, озер и водохранилищ, пустыни, степи, лесостепи, тундры;
B – городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м;
С – городские районы с застройкой зданиями высотой более 25 м.
Аэродинамический коэффициент с различен для различной формы здания и крыши, а также для направления ветра по отношению к этому сооружению. На рисунке 2.1 представлена схема для определения значения коэффициента для здания прямоугольной формы с плоской крышей, где стрелками показано направление ветра, а буква «α» определяет значение угла между направлением ветра и данной стеной здания. По таблице 2.2 находятся значения аэродинамического коэффициента. Знак «плюс» у коэффициентов соответствует направлению давления ветра на соответствующую поверхность, знак «минус» – от поверхности.
Таблица 2.1 – Значения коэффициента, учитывающего изменение ветрового давления по высоте
| Высота h, м | Коэффициент k для типов местности | ||
| А | В | С | |
| 0,75 1,00 1,25 1,50 1,70 1,85 2,00 2,25 2,45 2,65 2,75 2,75 2,75 | 0,50 0,65 0,85 1,10 1,30 1,45 1,60 1,90 2,10 2,30 2,50 2,75 2,75 | 0,40 0,40 0,55 0,80 1,00 1,15 1,25 1,55 1,80 2,00 2,20 2,35 2,75 |
Нормативное значение пульсационной составляющей ветровой нагрузки на высоте h определяется следующим образом
wp = wmZv,
где Z – коэффициент пульсаций давления ветра на уровне h, определяемый по таблице 2.3;
v – коэффициент пространственной корреляции пульсаций давления ветра.
Коэффициент v пространственной корреляции пульсаций давления определяется в зависимости от поверхности сооружения. Если расчетная поверхность близка к прямоугольнику, ориентированному так, что его стороны параллельны основным осям (рисунок 2.2), то коэффициент определяется по таблице 2.4 в зависимости от параметров X и Y, принимаемых по таблице 2.5.
|

|
Таблица 2.3 – Значения коэффициента пульсаций давления ветра
| Высота h, м | Коэффициент пульсаций давления ветра для типов местности | ||
| А | В | С | |
| 0,85 0,76 0,69 0,62 0,58 0,56 0,54 0,51 0,49 0,47 0,46 0,46 0,46 | 1,22 1,06 0,92 0,80 0,74 0,70 0,67 0,62 0,58 0,56 0,54 0,52 0,50 | 1,78 1,78 1,50 1,26 1,14 1,06 1,00 0,90 0,84 0,80 0,76 0,73 0,68 |
|
|
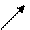
|
|
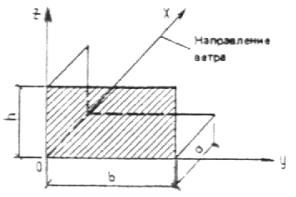
Рисунок 2.2 – Схема изображения стен здания по координатным осям
Таблица 2.4 – Значения коэффициент v пространственной корреляции пульсаций давления ветра
| Х, м | Y, м |
| 5 10 20 40 80 160 350 | |
| 0,1 | 0,95 0,92 0,88 0,83 0,76 0,67 0,56 0,89 0,87 0,84 0,80 0,73 0,65 0,54 0,85 0,84 0,81 0,77 0,71 0,64 0,53 0,80 0,78 0,76 0,73 0,68 0,61 0,51 0,72 0,72 0,70 0,67 0,63 0,57 0,48 0,63 0,63 0,61 0,59 0,56 0,51 0,44 0,53 0,53 0,52 0,50 0,47 0,44 0,38 |
Таблица 2.5 – Размеры здания
| Основная координатная плоскость, параллельно которой расположена расчетная поверхность | X | Y |
| zoy | b | h |
| zox | 0,4a | h |
| xoy | b | a |
Скорость ветра и ветровое давление зависят от высоты над землей. Для определения изменения скорости υ ветра по высоте h используется формула
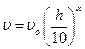 ,
,
где υо – скорость ветра на высоте 10 м, м/с;
α – показатель степени, зависящий от шероховатости подстилающей поверхности, воздухообмена между слоями и скорости ветра:
0,16 – для местности типа А;
0,28 – для местности типа В;
0,40 – для местности типа С.
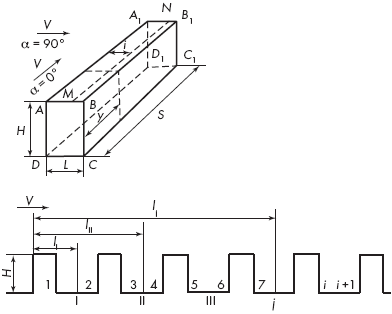
Значения ветрового давления зависят от расположения соседних зданий и сооружений. На рисунке 2.3 представлены шесть жилых зданий, расположенных параллельно. Здания даны торцом, высота каждого – Н. Промежутки между зданиями обозначены через I, II и так далее, расстояния между ними обозначены как l1, l11,…, li, соответственно, V – направление ветра.
При направлении воздушного потока вдоль зданий (α=0°) аэродинамические коэффициенты для поверхностей всех зданий практически не отличаются от коэффициентов, полученных для отдельных сооружений. При направлении воздушного потока перпендикулярно продольной оси зданий (α=90°) наветренная сторона первого здания испытывает давление, близкое давлению на стену отдельно стоящего здания. Пространство между первым и вторым зданием испытывает сильное подсасывающее действие ветра за счет первичного возмущения, возникающего при обтекании зданий воздушным потоком. Для остальных зданий влияние этого возмущения постепенно ослабевает. Для определения аэродинамического коэффициента в этом случае введен геометрический критерий


Рисунок 2.3 – Схема расположения шести зданий и направление ветра
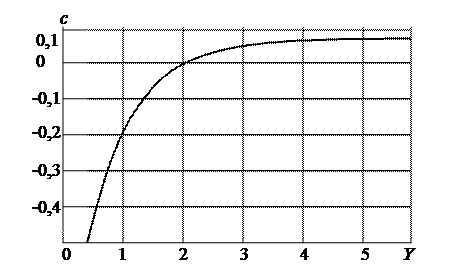 |
Рисунок 2.4 – График зависимости аэродинамического коэффициента от геометрического критерия
Задание 2.1. Определить изменение скорости течения воздуха при переходе из трубки тока с сечением S1=2500 м2 в трубку с сечением S2=1500 м2, если в первом сечении его скорость была равна υ1=4 м/с. Считать воздух не сжимаемым.
Решение. Согласно теореме о неразрывности потока можно записать
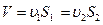 ,
,
где V – объем воздуха в трубке.
Скорость во втором сечение будет меняться и составит 6,6 м/с.
Ответ: υ2=6,6 м/с.
Таблица 2.6 – Задание 2.1 по вариантам
| № варианта | Площадь поперечного сечения первой части трубки, м2 | Площадь поперечного сечения второй части трубки, м2 | Скорость в первой части трубки, м/с |
Задание 2.2. Трубка тока имеет переменное сечение с площадями поперечного сечения 50 и 25 м2. Объем перемещаемого воздуха равен 100 м3 в одну секунду. Определить разность уровней воздуха в вертикальных ответвлениях одинакового размера, но находящихся в разных сечениях. Считать воздух не сжимаемым.
Решение. Уравнение Бернулли в этом случае имеет вид
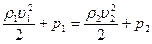 ,
,
где индексы 1 и 2 – части трубки тока с сечением 50 и 25 м2 соответственно;
р1 и р2 – давления в соответствующих частях трубки;
ρ1=ρ2 – плотности воздуха.
Согласно теореме о неразрывности потока можно записать
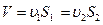 .
.
Перепад давления при переходе воздуха из одной части трубки в другую создает разность Δh уровней в вертикальных ответвлениях
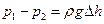 .
.
В результате совместного решения данных уравнений, получим разность уровней воздуха в вертикальных ответвлениях 0,6 м.
Ответ: Δh=0,6 м.
Таблица 2.7 – Задание 2.2 по вариантам
| № варианта | Площадь поперечного сечения первой части трубки, м2 | Площадь поперечного сечения второй части трубки, м2 | Объем перемещаемого воздуха, м3 |
Задание 2.3. Найти нормативное значение средней составляющей ветровой нагрузки на стену здания на высоте h=200 м при скорости ветра на высоте 10 м равной υо=6 м/с. Тип местности С. Ветер направлен на длинную сторону здания. Здание прямоугольной формы с плоской крышей.
Решение. Нормативное значение средней составляющей ветровой нагрузки определяется по формуле
wm=wokc,
а нормативное значение ветрового давления
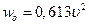 .
.
Скорость ветра на заданной высоте
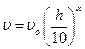 .
.
По таблицам 2.1 и 2,2 с учетом типа местности определяются значения коэффициентов: α=0,4; k=1,8; c=0,7. После вычислений получается величина, равная 306,2 Па.
Ответ: wm=306,2 Па.
Таблица 2.8 – Задание 2.3 по вариантам
| № варианта | Высота для вычисления ветровой нагрузки, м | Скорость ветра на высоте 10 м, м/с | Тип местности |
| А | |||
| В | |||
| А | |||
| В | |||
| С | |||
| А | |||
| В | |||
| С | |||
| А | |||
| В |
Задание 2.4. Найти пульсационную составляющую ветровой нагрузки на стену здания. Здание прямоугольной формы с плоской крышей. На рисунке 2.5 представлены направление ветра υв, схематическое изображение здания в координатных осях хуz, а также заштрихована расчетная поверхность (b=80 м). Значение нормативной средней составляющей ветровой нагрузки, расчетной высоты, тип местности берутся из задания 2.3.
Решение. Пульсационная составляющая ветровой нагрузки на высоте h определяется по формуле
wp = wmZv,
где Z=0,84 (по таблице 2.3);
wm=306,2 Па (по заданию 2.3).
Коэффициент v пространственной корреляции пульсаций давления ветра определяется следующим образом. Согласно рисунку 2.5 и таблице 2.5 расчетная поверхность лежит в плоскости zoy, тогда X=b=80 м, Y=h=200 м. По таблице 2.4 – ν=0,5.
Пульсационная составляющая получается равной 128,5 Па.
Ответ: wp=128,5 Па.
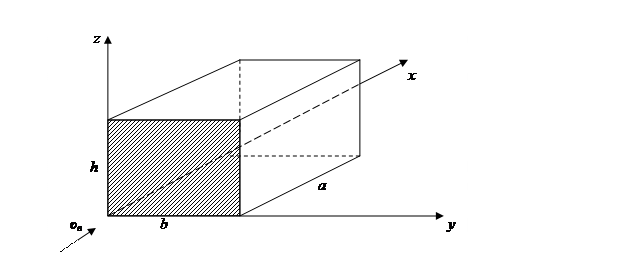
Рисунок 2.5 – Схема здания с координатными осями
Таблица 2.9 – Задание 2.4 по вариантам
| № варианта | а, м | b, м | Расчетная поверхность |
| zoy | |||
| zox | |||
| xoy | |||
| zoy | |||
| zox | |||
| xoy | |||
| zoy | |||
| zox | |||
| xoy | |||
| zox |
Задание 2.5. Найти нормативное значение средней составляющей ветровой нагрузки на стену здания, которое является четвертым по счету от здания, принимающего основное ветровое давление (рисунок 2.3). Тип местности, направление ветра, форма здания, нормативное значение ветрового давления, коэффициент, учитывающий изменение ветрового давления по высоте, высоту для определения давления ветра берутся из задания 2.3. Расстояние от первого дома до расчетного равно l=90 м, S=40 м (рисунок 2.3).
Решение. Нормативное значение средней составляющей ветровой нагрузки определяется по формуле
wm=wokc,
где wo=243 Па и k=1,8.
Аэродинамический коэффициент c находится через геометрический критерий
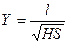 .
.
В этой формуле: Н=200 м, l=90 м, S=40 м. Далее по графику зависимости аэродинамического коэффициента от геометрического критерия (рисунок 2.4) находится аэродинамический коэффициент: Y=1 и с=-0,2 (знак «минус» соответствует направлению давления ветра от соответствующей поверхности).
После расчетов нормативное значение средней составляющей ветровой нагрузки получилось равным -87,5 Па.
Ответ: wm=-87,5 Па.
Таблица 2.10 – Задание 2.5 по вариантам
| № варианта | l, м | S, м |
