Классификация состояний цепи Маркова с дискретным временем

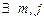Определение. Состояние цепи Маркова называется несущественным, если , такие что

, ,

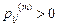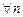
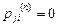то есть существует такое состояние 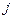, в которое можно попасть с положительной вероятностью, но из которого нельзя вернуться в 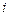. Здесь 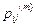- вероятность перехода цепи Маркова из состояния 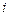в состояние 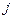за 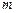шагов.

Если из множества 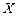выделить все несущественные состояния, то оставшееся множество существенных состояний обладает тем свойством, что, попав в него, цепь Маркова никогда из него не выйдет.

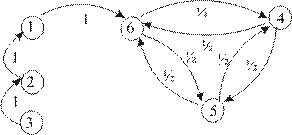
Рис. 1.

Как видно из рисунка, {1,2,3} – несущественные состояния, {4,5,6} – существенные.

Рассмотрим множество существенных состояний.

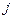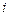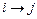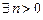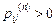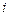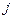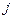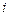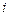Определение.Состояние называется достижимым из состояния (обозначается ), если , что . Состояния и называются сообщающимися (обозначается ), если достижимо из , и достижимо из .

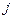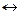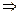
По определению отношение « » является симметричным ( 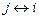), и нетрудно убедиться, что оно транзитивно ( ).

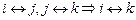Множество существенных состояний можно разбить на конечное или счетное число непересекающихся множеств 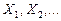состоящих из сообщающихся состояний и характеризующихся тем, что переходы между различными множествами невозможны.

Определение. Множества 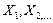называются замкнутыми классами, или неразложимыми классами, существенных сообщающихся состояний. Цепь Маркова, состояния которой образуют один неразложимый класс, называется неразложимой.

Пример.Рассмотрим цепь Маркова с множеством состояний 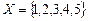и матрицей вероятностей переходов

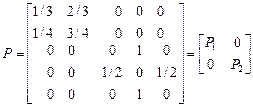
Граф вероятностей переходов имеет вид

Очевидно, что у рассматриваемой цепи все состояния существенные и есть два неразложимых класса 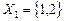, , 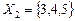и исследование ее свойств сводится к исследованию свойств каждой из двух цепей с матрицами вероятностей переходов соответственно 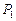и .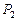

Проведенная классификация позволяет привести матрицу вероятностей переходов к каноническому виду. Для этого выделяют неразложимые классы, а также отдельно несущественные состояния. Тогда матрица P примет вид

,

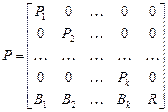где 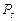– матрица вероятностей переходов 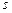-го неразложимого класса, 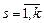; 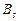– матрица вероятностей переходов из несущественных состояний в состояние 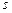-го замкнутого класса; 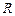– матрица вероятностей переходов по несущественным состояниям.