Проверка допустимости линейных невязок

№ ходов	S i + j, м	f x = x i - x j, м	f y = y i - y j, м	f абс, м	f отн
1 + 2
2 + 3

Вопросы для самопроверки

1. По какой формуле вычисляется дирекционный угол узловой линии при передаче его от твердой стороны по ходу с левыми углами? с правыми углами?

2. По какой формуле вычисляется окончательное значение дирекционного угла узловой линии?

3. Как вычисляется угловая невязка в ходе, если известны значения дирекционного угла узловой линии - окончательное и вычисленное по ходу, если углы в ходе левые? правые?

4. Как контролируется доброкачественность угловых измерений в сети?

5. По какой формуле вычисляется вес дирекционного угла узловой линии, полученный по ходу?

6. В чем состоит контроль правильности вычисления угловых невязок в ходах, сходящихся к узловой точке?

7. Как распределяются угловые невязки на углы в каждом ходе?

8. По какой формуле вычисляется вес координаты узловой точки, если координата получена по ходу от твердой точки?

9. По каким формулам вычисляются окончательные значения координат узловой точки?

10. Как вычисляются невязки в приращениях координат в каждом ходе, если известны значения координат узловой точки, вычисленные по ходу, и окончательные?

11. Как контролируется доброкачественность измерений в системе ходов?

12. В чем состоит контроль правильности вычисления невязок в приращениях координат по каждому ходу?

13. Как распределяются невязки в приращениях координат внутри каждого хода?

ОПРЕДЕЛЕНИЮПРЯМОУГОЛЬНЫХ

КООРДИНАТ ОТДЕЛЬНЫХ ПУНКТОВ

СОСТАВ РАБОТЫ

В состав работы входит решение следующих задач:

- снесение прямоугольных координат с вершины знака на землю;

- определение координат отдельного пункта прямой засечкой (формулы Гаусса);

- определение координат отдельного пункта прямой, засечкой (формулы Юнга);

- определение координат отдельного пункта обратной засечкой (формулы Кнейсселя);

- определение координат отдельного пункта линейной засечкой.

Пояснения к лабораторной работе построены по следующему принципу:

- кратко изложена идея задачи, определены исходные данные и измеренные величины;

- приведены в аналитическом виде формулы решаемой задачи;

- раскрыт ход решения задачи по отдельным этапам;

- решение задачи иллюстрировано числовым примером;

- выполнена оценка точности определения дополнительного пункта.

ОБЩИЕ СВЕДЕНИЯ О СНЕСЕНИИ

ПРЯМОУГОЛЬНЫХ КООРДИНАТ С ВЕРШИНЫ

ЗНАКА НА ЗЕМЛЮ

При производстве топографо-геодезических работ в городских условиях невозможно бывает установить теодолит на пункте геодезической сети (пунктом является церковь, антенна и т. п.). Тогда и возникает задача по снесению координат пункта триангуляции на землю для обеспечения производства геодезических работ на данной территории.

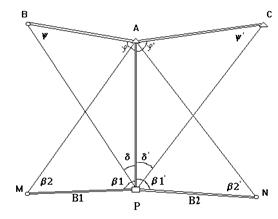
Схема решения задачи представлена на рис. 5.1.

Рис 5.1

Исходные данные: пункт А с координатами х_А, у_А; пункты геодезической сети В (х_В, у_В) и С (х_С, у_С).

Полевые измерения: линейные измерения выбранных базисов B1 и B2; измерения горизонтальных углов b1, b2; b1¢, b2¢; d, d¢.

Требуется найти: координаты точки Р - Хр, Уp.

Решение задачи разделяется на следующие этапы:

1) Определение недоступного расстояния - D_AP. Из треугольников АМР и АNР по теореме синусов получим:

D₁ =B₁ sinb₂ / sin(b₁+b₂), D₂ = B₂ sinb₂¢ / sin(b₁¢+b₂¢).

Разность (D₁ - D₂ ) не должна превышать величины 2D / T,

где 1 / T - относительная погрешность линейных измерений. D = (D₁ + D₂) / 2 окончательное значение.

2) Определение дирекционных углов a_ABи a_АC, а также расстояний S_AB и S_AC. Эти элементы находятся из решения обратных задач между пунктами А и B, А и С.

tg a_AB= (Y_B- Y_A) / (X_B- X_A), tg a_AC= (Y_C- Y_A) / (X_C- X_A),

по значениям тригонометрических функций находят значения румбов; знаки DY и DX определяют четверть, в которой находится направление, после чего вычисляются дирекционные углы a_ABи a_АC. Расстояния находят по формулам:

S_AB= (Y_B- Y_A) / sin a_AB; S_AC= (Y_C- Y_A) / sin a_AC

Для контроля, вычисления производят через (X_B- X_A) и (X_C- X_A).

3) Вычисление дирекционного угла направления АР - a_AP

Решение числового примера

Таблица5.1

Исходные данные

Обозначения	A XA, YA	B XB, YB	C XC, YC	B1 B2	b2 b¢2	b1 b¢1	d d¢
Численные значения	6327.46	8961.24	5604.18	266.12	38°26¢00¢¢	70°08¢54¢¢	138°33¢49¢¢
12351.48	10777.06	7125.76	198.38	42°26¢36¢¢	87°28¢00¢¢	71°55¢02¢¢

Таблица 5.2

Вычисление расстояния D_AP

Обозначения	B1 B2	sin b2 sin b¢2	sin(b1+b2) sin(b¢1+b¢2)	B1 sinb2 B2 sinb¢2	D1 D2	D1 - D2 2D / T	D ср
Численные значения	266.12	0.62160	0.94788	165.420	174.52	0.00	174.52
198.38	0.67482	0.76705	133.871	174.52

Таблица 5.3

Решение обратных задач

Обозначения	YB YA	XB XA	YC YA	XC XA	tg aAB aAB	tgaAC aAC	sin aAB sin aAC cos aAB cos aAC	SAB     SAC
численные значения	10777.06	8961.24	7125.66	5605.08	- 0.5977	7.23421	-0.51309	3068.48
12351.48	6327.46	12351.48	6327.46	329°07¢55¢¢	262°07¢51¢¢	-0.99058	5275.51
						0.85833
						-0.13693

Таблица 5.4

Вычисление дирекционных углов a_AP= a_D

Обозначения	D	sin d sin d¢	S AB S AC	sin y sin y¢	y y¢	j j¢	aAB aAC	aD a¢D	aD- a¢D smb
численные значения	174.52	0.66179	3068.48	0.03950	...	39°10¢41¢¢	329°07¢55¢¢	8°18¢36¢¢	Da=1¢¢
	0.95061	5275.51	0.03292	...	106°11¢46¢¢	262°07¢51¢¢	8°18¢37¢¢	30¢¢

Вычисление складывается из следующих этапов:

а) вычисление вспомогательных углов y и y¢ по теореме синусов из треугольников АВР и АСР:

sin y = D×sind / S_AB, sin y¢ = D×sind¢ / S_AC;

б) вычисление углов j и j¢ по формулам:

j = 180° - (d + y), j¢ = 180° - (d¢ + y¢);

в) вычисление двух значений дирекционного угла:

a_D= a_AB± j, a_D¢ = a_AС± j¢

Контролем служит выражение (a_D- a¢_D) £ sm_b,

где m_b- СКП измерения горизонтальных углов. Знак «+» или « - » в формулах вычисления дирекционного угла берется в зависимости от взаимного расположения пунктов А, Р, В и С.

4) Вычисление координат точки Р

Координаты вычисляются путем решения прямой геодезической задачи между пунктами А и Р по формулам:

X_P= X_A+ DX, Y_P= Y_A+ DY;

X¢_P= X_A+ DX¢, Y¢_P= Y_A+ DY¢.

Приращения координат вычисляются по двум значениям дирекционного угла a_D , что обеспечивает соответствующий контроль:

DX = D cos a_D, DY = D sin a_D;

DX¢ = D cos a¢_D, DY¢ = D sin a¢_D.

Расхождение координат не должно превышать величины sm_b×D / r, где r = 206265¢¢, m_b- средняя квадратическая погрешность измерения углов.

Таблица 5.5