По методу Бубнова – Галеркина

Метод Бубнова - Галеркина основан на основе принципа Лагранжа: сумма работ всех внутренних и внешних сил упругой системы на любых малых возможных перемещениях равняется нулю .

За основу берём уравнение равновесия пластины, в безразмерном виде имеющее форму (3). Данное уравнение представляет собой проекцию на ось 6 всех внешних и внутренних сил, действующих на бесконечно малый элемент пластины. Функция прогиба представляет собой 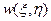представляет собой перемещение в направлении этой же оси. Если подставить выражение для w (5) и (3), получим:

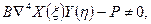(31)

так как выражение (5) не является решением уравнения (3).

Составляем вариационное уравнение метода Бубнова - Галеркина, выражающее равенство нулю суммы работ всех внешних и внутренних сил пластины на возможных перемещениях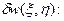

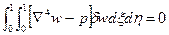(32)

Подставим (5) в (32) и получаем

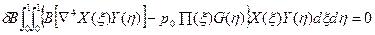(33)

Из (33) находим выражение для амплитуды прогиба

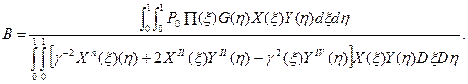(34)

Для нахождения параметра. В вычисляем определённые двойные интегралы, входящие в формулу (34). Проще всего сделать это следующим образом. Входящие в (34) двойные интегралы представляем в виде произведения одинарных интегралов, например:

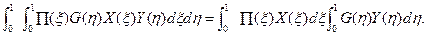(35)

Всего оказывается необходимым вычислить следующие 8 интегралов:

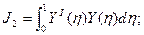
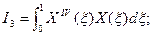
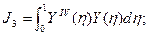
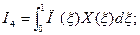
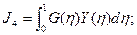
В качестве примера рассмотрим пластину (μ=0.3, γ=1), изображенную на рис.7. Построим для нее статическим методом В.З. Власова аппроксимирующие функци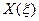и и 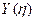имеют вид

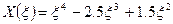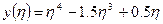, (36)

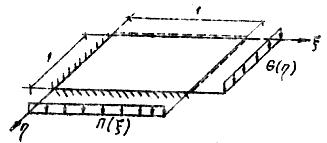
Рис.7

Нагрузка равномерно распределена по пластине, поэтому . Подставляя функции в формулы (35), вычисляем значения определенных интегралов: , , , .

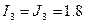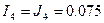Отметим, что раньше равенства (k=1.2.3.4) получены потому, что пластина симметричная относительно диагонали, проходящей через точки ξ=1, h=0-ξ=0, h=1. В общем же случае произвольной пластины .

Подставляем вычисленные значения интервалов в формулу (34) и получаем выражение для В

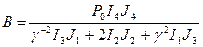. (37)

Для нашего примера получено В = 0.134 Р₀, теперь выражение для 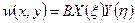полностью определено.