При выполнении заданий 21–26 используйте Бланк ответов №2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво
Вариант по математике № 1
Инструкция по выполнению работы
Общее время экзамена – 235 минут.
Характеристика работы. Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть 1), 4 задания повышенного уровня (часть 2) и 2 задания высокого уровня сложности (часть 2). Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика».
Модуль «Алгебра» содержит 11 заданий: в части 1 – восемь заданий;
в части 2 – три задания. Модуль «Геометрия» содержит восемь заданий:
в части 1 – пять заданий; в части 2 – три задания. Модуль «Реальная математика» содержит семь заданий: все задания этого модуля – в части 1.
Советы и указания по выполнению работы. Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте
в черновике. Записи в черновике не учитываются при оценивании работы. Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Ответы к заданиям 2, 3, 8, 14 записываются в виде одной цифры, которая соответствует номеру правильного ответа. Эту цифру запишите в поле ответа в тексте работы.
Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.
Все ответы первой части перенесите в Бланк ответов №1.
Решения заданий части 2 и ответы к ним запишите в Бланке ответов №2. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.
При выполнении работы Вы можете воспользоваться справочными материалами.
Оценивание работы. Баллы, полученные за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, из них не менее 3 баллов в модуле «Алгебра», не менее 2 баллов в модуле «Геометрия» и не менее 2 баллов
в модуле «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2, 3 и 4 балла.
Желаем успеха!
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения 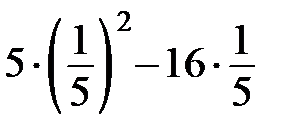 .
.
Ответ: ___________________________.
2. На координатной прямой отмечены числа 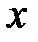 ,
, 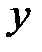 и
и 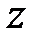 .
.
Какая из разностей 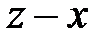 ,
, 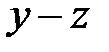 ,
, 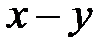 отрицательна?
отрицательна?
| 1) | 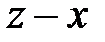 |
| 2) | 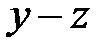 |
| 3) | 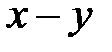 |
| 4) | ни одна из них |
| Ответ: |
3. Значение какого из данных выражений является наибольшим?
| 1) | 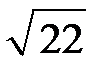 | 2) | 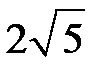 | 3) | 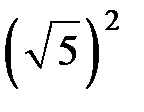 | 4) | 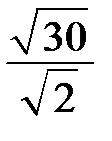 |
| Ответ: |
4. Найдите корень уравнения 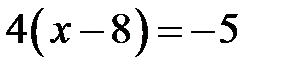 .
.
Ответ: ___________________________.
5. Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
| А) | Б) | В) | ||
ФОРМУЛЫ
| 1) | 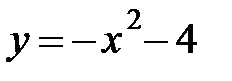 | 2) | 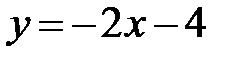 | 3) | 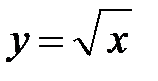 |
В таблице под каждой буквой укажите соответствующий номер.
| Ответ: | А | Б | В |
6. Выписаны первые несколько членов арифметической прогрессии: 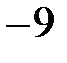 ;
; 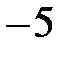 ;
; 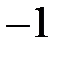 ; … Какое число стоит в этой арифметической прогрессии на 91-м месте?
; … Какое число стоит в этой арифметической прогрессии на 91-м месте?
Ответ: ___________________________.
7. Найдите значение выражения 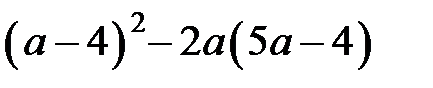 при
при 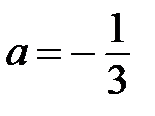 .
.
Ответ: ___________________________.
8. Решите неравенство 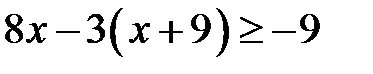 .
.
| 1) | 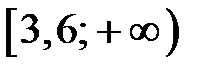 |
| 2) | 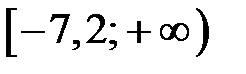 |
| 3) | 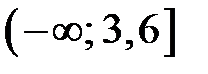 |
| 4) | 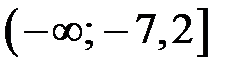 |
| Ответ: |
Модуль «Геометрия»
9. Один из острых углов прямоугольного треугольника равен 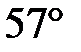 . Найдите его другой острый угол. Ответ дайте в градусах.
. Найдите его другой острый угол. Ответ дайте в градусах.
Ответ: ___________________________.
10. Четырёхугольник 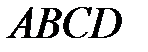 вписан в окружность. Угол
вписан в окружность. Угол 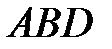 равен
равен 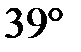 , угол
, угол 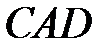 равен
равен 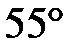 . Найдите угол
. Найдите угол 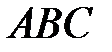 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Ответ: ___________________________.
11. Найдите площадь параллелограмма, изображённого на рисунке.
Ответ: _____________________.
12. На клетчатой бумаге с размером клетки 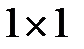 отмечены три точки: отмечены три точки: 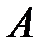 , , 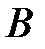 и и  . Найдите расстояние от точки . Найдите расстояние от точки 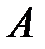 до середины отрезка до середины отрезка 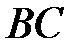 . . |
Ответ: ___________________________.
13. Какое из следующих утверждений верно?
| 1) | Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. |
| 2) | В параллелограмме есть два равных угла. |
| 3) | Площадь прямоугольного треугольника равна произведению длин его катетов. |
В ответ запишите номер выбранного утверждения.
Ответ: ___________________________.
Модуль «Реальная математика»
14. В таблице даны результаты забега девочек 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,8 с.
| Номер дорожки | I | II | III | IV |
| Время (в с) | 10,7 | 10,9 | 9,8 | 11,4 |
Укажите номера дорожек, по которым бежали девочки, получившие зачет.
| 1) | только II |
| 2) | II, IV |
| 3) | только III |
| 4) | I, III |
| Ответ: |
15. При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 15 часов работы фонарика. Ответ дайте в вольтах.
Ответ: ___________________________.
16. Плата за телефон составляет 210 рублей в месяц. В следующем году она увеличится на 15%. Сколько рублей придётся платить ежемесячно за телефон в следующем году?
Ответ: ___________________________.
17. Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большей опоры 2,85 м. Найдите высоту средней опоры. Ответ дайте в метрах.
Ответ: ___________________________.
18. На диаграмме показан возрастной состав населения Греции. Определите по диаграмме, население какого возраста преобладает.
| 1) | 0–14 лет |
| 2) | 15–50 лет |
| 3) | 51–64 лет |
| 4) | 65 лет и более |
В ответе запишите номер выбранного варианта ответа.
Ответ: ___________________________.
19. У бабушки 20 чашек: 15 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Ответ: ___________________________.
20. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 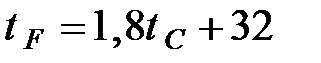 , где
, где 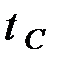 – температура в градусах Цельсия,
– температура в градусах Цельсия, 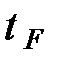 – температура в градусах Фаренгейта. Какая температура по шкале Фаренгейта соответствует
– температура в градусах Фаренгейта. Какая температура по шкале Фаренгейта соответствует 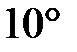 по шкале Цельсия?
по шкале Цельсия?
Ответ: ___________________________.
Все ответы первой части перенесите в Бланк ответов №1.
Часть 2
При выполнении заданий 21–26 используйте Бланк ответов №2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Модуль «Алгебра»
21. Сократите дробь 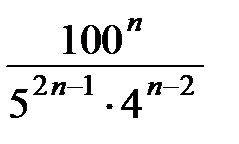 .
.
22. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 9 км/ч, а вторую половину пути проехал со скоростью 60 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
23. Постройте график функции 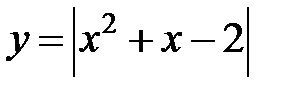 . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Модуль «Геометрия»
24. Точка 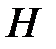 является основанием высоты
является основанием высоты 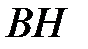 , проведённой из вершины прямого угла
, проведённой из вершины прямого угла 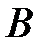 прямоугольного треугольника
прямоугольного треугольника 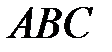 . Окружность с диаметром
. Окружность с диаметром 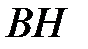 пересекает стороны
пересекает стороны 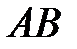 и
и 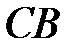 в точках
в точках 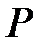 и
и 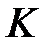 соответственно. Найдите
соответственно. Найдите 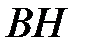 , если
, если 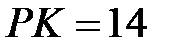 .
.
25. Биссектрисы углов 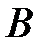 и
и  параллелограмма
параллелограмма 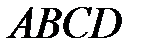 пересекаются в точке
пересекаются в точке 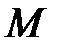 стороны
стороны 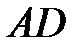 . Докажите, что
. Докажите, что 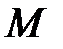 – середина
– середина 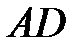 .
.
26. На стороне 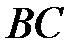 остроугольного треугольника
остроугольного треугольника 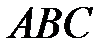 (
( 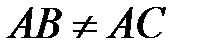 ) как на диаметре построена полуокружность, пересекающая высоту
) как на диаметре построена полуокружность, пересекающая высоту 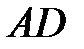 в точке
в точке 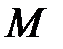 ,
, 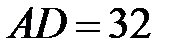 ,
, 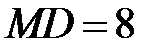 ,
, 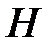 – точка пересечения высот треугольника
– точка пересечения высот треугольника 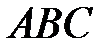 . Найдите
. Найдите 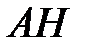 .
.
