Изображение шара и его сечений

1. Изображение шара. Пусть F₀ – шар. Выберем направление проектирования и рассмотрим касательные к шару, принадлежащие выбранному направлению. Эти касательные образуют цилиндрическую поверхность и проходят через точки большой окружности шара, плоскость которой перпендикулярна направлению проектирования.

Выберем плоскость изображения. В общем случае цилиндрическая поверхность пересечет эту плоскость по эллипсу, а проекция F₁ шара F₀ будет частью плоскости, ограниченной этим эллипсом. Такое изображение шара не является наглядным (рис. 59). Если плоскость изображения выбрать перпендикулярной направлению проектирования, то изображением шара будет круг F. Круг, конечно, дает о шаре более наглядное представление, но в круг можно спроектировать и равный ему круг, и цилиндр (если проектирование вести параллельно его образующим).

Прежде чем продолжить разговор о том, как сделать изображение шара наглядным, вспомним известные со школы понятия, связанные с шаром. Сечение шара плоскостью, проходящей через центр шара, называется большим кругом, а его окружность – экватором. Точки пересечения прямой, перпендикулярной плоскости экватора, с поверхностью шара называются полюсами, соответствующими этому экватору, а соединяющий их диаметр – полярной осью.

Если на проекционном чертеже шара изобразить какой-либо экватор и соответствующие ему полюсы, то у изображения появится объемность. Оно станет наглядным.

Какой экватор изображать? Во-первых, желательно, чтобы отрезок, соединяющий изображения полюсов, был на чертеже вертикальным. Это желание будет выполнено, если плоскость изображения p будет вертикальной, а плоскость a, проходящая через полюсы N₀, S₀ шара, – ей перпендикулярной и тоже вертикальной. (Напомним, что мы договорились использовать ортогональное проектирование.) Более того, можно считать, что плоскость изображения p проходит через центр шара, и, значит, пересекает его по окружности большого круга. Эту окружность обычно называют очерковой окружностью шара.

Обозначим точки пересечения прямой 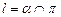с поверхностью шара буквами P₀ и Q₀. Если плоскость экватора также выбрать перпендикулярной плоскости p, то экватор и диаметр, соединяющий полюсы, изобразятся перпендикулярными диаметрами окружности (рис. 60) и изображение шара не станет нагляднее. Поэтому плоскость экватора не должна быть перпендикулярной плоскости изображения. На рис. 61 дано сечение шара плоскостью a. На этом рисунке P₀Q₀ – прямая пересечения плоскостей a и p; C₀D₀ – пересечение a и экваториального круга, N₀S₀ – диаметр, соединяющий полюсы. При проектировании на плоскость p полюсы N₀ и S₀ спроектируется в точки N и S соответственно, диаметр C₀D₀ экватора – в малую ось 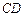эллипса, изображающего этот экватор.

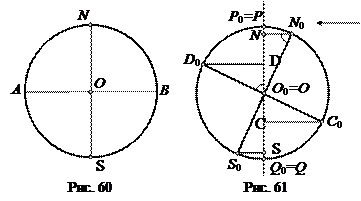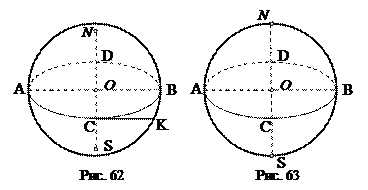
Большая ось 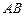эллипса (рис. 62) будет проекцией диаметра 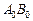экватора, перпендикулярного диаметру 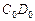и, следовательно, параллельного плоскости .

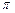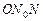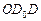Чтобы указать положение полюсов, вернемся к рис. 61. Прямоугольные треугольники и на этом рисунке равны по гипотенузе и острому углу (углы с соответственно перпендикулярными сторонами). Поэтому 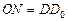. Но в свою очередь 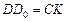, где 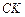– отрезок касательной к эллипсу, изображающему экватор (рис. 62).

Итак, наглядное изображение шара можно построить следующим образом:

1) Строим эллипс, который принимаем за изображение экватора, и его оси.

2) Проводим окружность с центром в центре эллипса, радиус которой равен большой полуоси эллипса.

3) Строим отрезок касательной к эллипсу, параллельные его большой оси, а затем изображения полюсов.

На рис. 63 показана достаточно типичная ошибка, когда полюсы изображаются на очерковой окружности, а экватор при этом изображен эллипсом.

2. Изображение параллелей и меридианов. Рассмотрим изображение полюсов и меридианов сферы, являющейся поверхностью шара. Напомним, что параллелями сферы называются ее сечения плоскостями, параллельными плоскости экватора. Сечения сферы плоскостями, проходящими через полярную ось, называются меридианами.

Через каждую точку сферы, отличную от полюса, проходит точно один меридиан и одна параллель. Каждый меридиан проходит через оба полюса.

Параллели и меридианы являются окружностями, поэтому также изображаются эллипсами.

Начнем с изображения параллелей. Параллель будет определена, если задать точку, в которой ее плоскость пересекает полярную ось. Поскольку плоскость параллели параллельна плоскости экватора, изображением параллели будет эллипс, подобный эллипсу, изображающему экватор.

Для построения этого эллипса рассмотрим сечение сферы (шара) плоскостью, проходящей через полярную ось 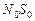перпендикулярно плоскости изображения (правая часть рис. 64). Построенное вспомогательное сечение позволяет легко найти малую ось эллипса, изображающего экватор, и изображения соответствующих ему полюсов.

Пусть параллель задана точкой 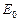, тогда плоскость параллели пересекает шар по отрезку 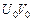, перпендикулярному оси 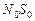. Этот отрезок равен большой оси 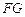эллипса, являющегося изображением параллели. Малая ось 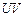находится с помощью проектирования точек 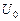, 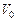на прямую 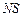. Наконец, с помощью прямой 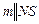находятся точки 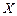, 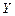касания изображения параллели с очерковой окружностью. Точки 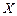, 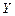разделяют видимую и невидимую части изображения параллели.

При построении эллипса, являющегося изображением параллели, совсем не обязательно строить эллипс, являющийся изображением экватора, которому он подобен. Более того, можно отдельно не выполнять и построение вспомогательного сечения (рис. 65).

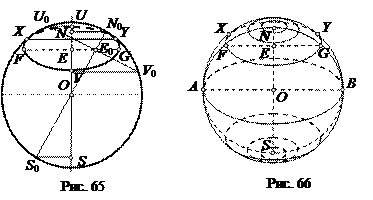
Как можно увидеть из рис. 66, в каждом из полушарий можно построить по эллипсу-параллели, которые касаются очерковой окружности только в одной точке. В верхнем полушарии изображения параллелей, лежащих севернее такой параллели будут полностью видимыми, а в нижнем полушарии изображения параллелей, лежащих южнее такой параллели – полностью невидимыми.

Задача. Построить изображение цилиндра, вписанного в шар, если высота цилиндра равна радиусу шара.

Решение. Построим изображение очерковой окружности шара и на ее вертикальном диаметре отметим изображения полюсов (рис. 67).

На этом же диаметре строим изображения центров 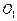, 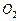оснований цилиндра. Из условия задачи 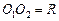, где 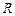– радиус шара, равный радиусу очерковой окружности. Поэтому 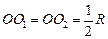. Тем самым задано положение параллелей. В соответствии с рассмотренными правилами строим эллипс-изображение верхнего основания. Эллипс, изображающий нижнее основание, можно получить с помощью параллельного переноса на вектор .

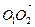В заключение рассмотрим, как строится изображение меридианов, если задано изображение сферы, ее экватора и соответствующих ему полюсов.

Пусть задано изображение 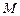точки 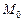, через которую проходит изображаемый экватор (рис. 68). В оригинале диаметр 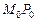перпендикулярен полярной оси 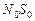, поэтому отрезки 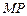, 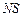являются сопряженными диаметрами эллипса, изображающего рассматриваемый меридиан. Значит, эллипс – изображение меридиана – по этим сопряженным диаметрам можно построить.

При построениях меридиана «от руки» обычно дополнительно ищут точки 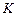, 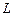касания эллипса с очерковой окружностью (рис.68). Диаметр 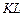очерковой окружности для эллипса будет большой осью, причем 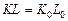, а значит, диаметр сферы 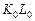параллелен плоскости проекции.

Точк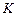и и 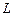можно найти из следующих соображений. Построим диаметр 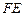эллипса-экватора, сопряженный диаметру 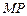. В оригинале 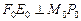, , 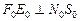поэтому диаметр 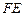перпендикулярен плоскости рассматриваемого меридиана. Отсюда следует, что 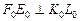, но тогда и 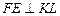(проектирование ортогональное). Точк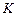и и 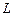разделяют видимую и невидимую части изображения меридиана.

Изображение теней

Иногда для придания чертежу большей наглядности используют тени. Кроме того, построение теней – интересная геометрическая задача, способствующая развитию пространственного мышления, сущность которой состоит в следующем.

Пусть из светящейся точки 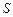прямолинейно во всех направлениях распространяются лучи света. Если луч встречает на своем пути непрозрачное тело 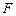, то он задерживается на нем и не доходит до некоторого экрана 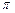. На последнем при этом образуется темная область 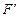, которую называют падающей тенью от тела 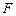(рис. 69).

Само тело 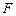при этом также оказывается разделенным на две части: освещенную и темную (неосвещенную). Темную часть тела называют его собственной тенью.

Границу падающей тени образуют точки пересечения с экраном лучей, касающихся поверхности тела 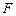и образующих световой конус с вершиной точке 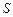. Линия, вдоль которой эти лучи касаются поверхности тела, называется линией раздела света и тени.

В случае, представленном на рис. 69, освещение называется факельным, такое же название имеет и соответствующая тень. Подобного рода освещение возникает при использовании источников искусственного освещения: электрической лампочки в комнате, фонаря на улице, пламени свечи и т.п.

Можно считать, что естественные источники (солнце, луна) находятся в бесконечности и лучи от них являются параллельными. Поэтому освещение, производимое пучком параллельных лучей, называют солнечным. Солнечное освещение показано на рис. 70.

Для того чтобы перейти к задачам на построение теней, условимся о том, как будем задавать лучи света на проекционном чертеже. При солнечном освещении такой световой луч можно задать прямой 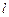и ее проекцией 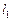на основную плоскость 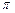(рис. 71). Пусть требуется построить падающую тень от точки 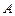на основную плоскость (экран). Чтобы сама точка 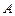была определена, необходимо указать ее проекцию 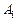на основную плоскость. Построение тени сводится к отысканию точки пересечения 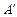прямой, проходящей через точку 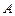параллельно 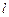, и прямой, проходящей через точку 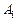параллельно 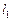. Заметим, что при этом отрезок 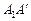является падающей тенью отрезка .

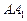При факельном освещении на проекционном чертеже надо задать точку, являющуюся световым источником. Она определяется точкой 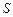и ее проекцией 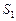на основную плоскость 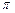(рис. 72). Здесь падающая тень 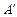точки 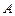– точка пересечения прямых 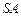и .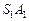

Ясно, что в качестве экрана можно выбирать не только основную плоскость. Наиболее интересные случаи построения теней имеют место именно тогда, когда приходится строить падающие тени на другие плоскости. (Например, падающую тень одного многогранника на поверхность другого.)

Задача 1. На рис. 73 изображены треугольная пирамида, ее высота и параллелепипед. Построить собственные и падающие тени этих непрозрачных фигур при заданном освещении.

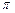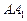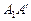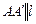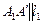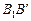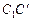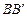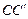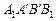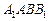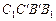Решение. Имеем дело с солнечным освещением. Прежде всего, найдем падающую тень параллелепипеда на основной плоскости . Падающей тенью ребра является отрезок , где , . Аналогично находятся падающие тени , ребер , соответственно. Отсюда следует, что – падающая тень грани , а – падающая тень грани 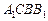(частично закрыта изображением параллелепипеда). Попутно отметим, что 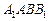– собственная тень параллелепипеда.

Чтобы найти падающие тени пирамиды на гранях параллелепипеда, найдем сначала ее падающую тень на основной плоскости 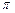. Это треугольник 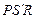( 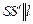, 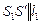), треугольник 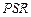будет собственной тенью пирамиды. Проектирующая плоскость 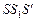прямой 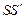пересекает грань 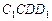параллелепипеда по отрезку 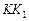. Проведя через точку 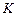прямую, параллельную 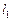, находим падающую тень 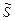вершины 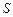на верхнем основании параллелепипеда. Прямые 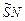, , 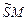проходящие через точку 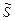параллельно прямым 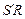, 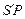соответственно, определяют падающую тень 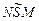пирамиды на верхнем основании параллелепипеда.

Остается найти падающую тень на боковой грани 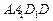параллелепипеда. Для этого заметим, что 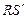– след плоскости 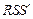на основной плоскости. Грань 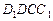пересекает след в точке 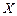, а точка 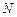принадлежит плоскостям 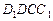и 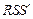. Отсюда заключаем, что плоскость 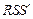пересекает боковое ребро 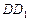параллелепипеда в точке 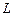, и строим падающую тень 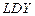пирамиды на грани .

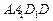В практике возможны случаи построения теней фигур, освещенных несколькими источниками света. Рассмотрим, например, освещение двумя источниками. В этом случае образуются две собственных и две падающих тени, которые могут налагаться друг на друга. Общая часть двух падающих теней, т.е. тень, затененная от двух источников, называется полной тенью фигуры. Непересекающиеся части теней называются полутенями. Полутени по насыщенности менее интенсивны, чем полная тень, поскольку лучи каждого из источников света освещают соответствующую часть тени, образованной другим источником.

Задача 2. Построить собственную и падающую тень непрозрачного куба, освещенного двумя факельными источниками.

Решение. Пусть на проекционном чертеже куба первый световой источник задан точкой 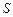и ее проекцией 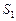на основную плоскость 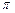, второй источник – точкам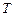и и 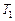(рис. 75).

Найдем падающую тень ребра 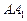куба на основную плоскость 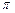от первого источника. Для этого достаточно найти падающую тень вершины 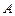, это точка 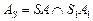. Аналогично ищутся падающие тени 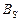, 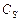вершин 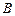, 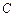соответственно. Значит, падающей тенью грани 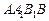служит четырехугольник 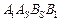, а падающей тенью грани 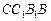– четырехугольник 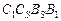, который частично закрыт изображением куба. Падающая тень куба от первого источника света найдена. Собственной тенью куба от этого источника является на изображении грань .

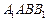Падающая тень от второго светового источника – многоугольник 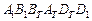– находится аналогично. Собственной тенью куба от этого источника будут гран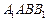и и .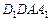

Полная тень, т.е. общая часть падающих теней от разных источников света, на чертеже выделена более темной заливкой.