Введение. Цель работы: определение коэффициента жесткости пружины динамическим и статическим методом

Лабораторная работа № 21

ИССЛЕДОВАНИЕ ПРУЖИННОГО МАЯТНИКА

Цель работы: определение коэффициента жесткости пружины динамическим и статическим методом. Исследование зависимости коэффициента силы трения от радиуса шарика.

Приборы и принадлежности: ПК с установленной моделирующей и управляющей программой.

Литература:

1. Теория колебаний пружинного маятника изложена в описании, выложенном на рабочем столе ПК.

2. Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика. – М.: Наука, 1982, гл. VII, § 49, 50, 53, 58.

3. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. т. 2 – М.: Наука, 1991, гл. VIII, § 1 – 3.

Введение

Колебанияминазываются процессы, обладающие той или иной степенью повторяемости. Простейшим видом колебаний являются гармонические колебания, т. е. колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса

.

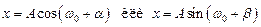Амплитудойколебания называется абсолютная величина наибольшего отклонения системы от положения равновесия. Амплитудаона зависит от энергии, сообщенной колебательной системе в начальный момент времени.

Периодом колебанийназывается величина, численно равная минимальному промежутку времени, через который состояния колебательной системы повторяются, обозначается буквой Т.

Величина, равная числу колебаний, совершенных в единицу времени, называется частотой колебаний n.

Частота и период связаны между собой соотношением:

.

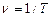Собственная циклическая или круговая частота и период колебаний связаны соотношением

.

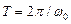Рассмотрим пружинный маятник – систему, состоящую из шарика массы m, подвешенного на пружине, масса которой пренебрежимо мала по сравнению с m. В положении равновесия сила тяжести 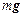и сила упругости пружины 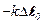, приложенные к грузу, компенсируют друг друга.

,

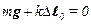где k – коэффициент жесткости пружины, 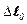– удлинение пружины в равновесии. Будем характеризовать смещение шарика из положения равновесия координатой x, причем ось x направим по вертикали вниз, а начало отсчета совместим с положением равновесия груза.

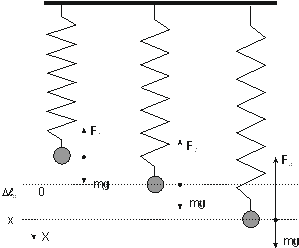Рис 21.1. Для удобства центр тяжести шарика смещен по горизонтали.

Если сместить шарик в положение, характеризуемое координатой x, то удлинение пружины станет равно 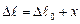, равновесие нарушится, и уравнение второго закона Ньютона для шарика имеет вид:

.

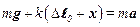Вычитая из (21.3) уравнение (21.2) получим:

.

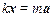Используя определение ускорения и проецируя на ось Х, приходим к уравнению

,

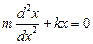решением этого дифференциального уравнения является функция вида

.

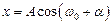где a – начальная фаза, w₀ - собственная частота колебаний.

Из формулы (21.5) следует, что груз, подвешенный на пружине, в отсутствии сил сопротивления совершает гармонические колебания.