Нелинейное программирование

Общая задача нелинейного программированияимеет вид:

,

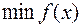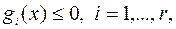(6.6.1)

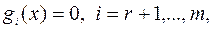
где все функции предполагаются дифференцируемыми.

1. Необходимые условия минимума.Для произвольной допустимой точки 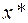введем множества индексов

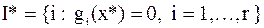, (активные ограничения неравенства)

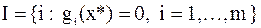, (все активные ограничения). (6.6.2)

Теорема 21(Каруш-Джон). Пусть 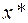– точка локального минимума в (6.6.1), а функции 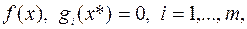непрерывно дифференцируемы в окрестности 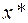. Тогда найдутся числа 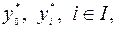не все равные 0, такие, что 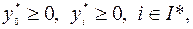и

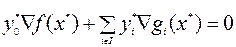. (6.6.3)

Введемфункцию Лагранжа

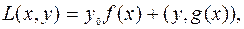
где , .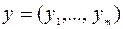

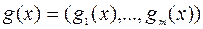Выражение (6.6.3) называется условием стационарности. Его можно записать в виде

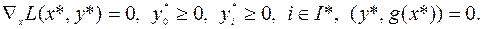(6.6.3)

Согласно теореме 1 в точке локального минимума должны выполняться условия:

1) условия стационарности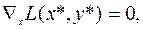

2) условия допустимости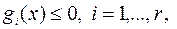

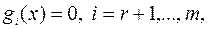
3) условия неотрицательности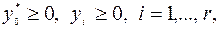

4) условие нетривиальности ,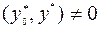

5) условие дополняющей нежесткости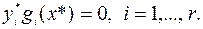

Перечисленные условия дают сумму соотношений, которые необходимо выполнить при поиске возможных точек минимума.

Сформулируем условия, при которых можно гарантировать .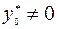

Условие регулярности. Векторы 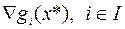, линейно независимы.

Теорема 22.Пусть 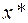– точка локального минимума в (6.6.1), функции 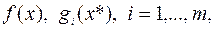непрерывно дифференцируемы в окрестности 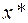, и выполнены условия регулярности. Тогда найдутся числа 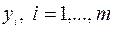, такие, что

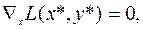
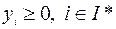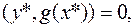, (6.6.4)

где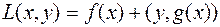

2. Достаточные условия минимума для некоторой точки позволяют утверждать, что она является точкой минимума.

Теорема 23.Пусть 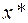– допустимая точка, функции 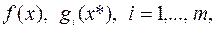дважды дифференцируемы в 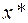. Пусть для некоторого 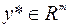выполняется (6.6.4) и для некоторого 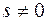, для которого

, ,

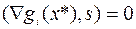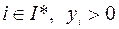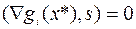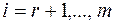, , (6.6.5)

, ,

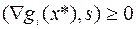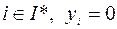выполняется неравенство

.

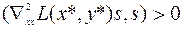Тогда 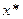– точка локального минимума в задаче (6.6.1).

Пример 1.Пусть требуется решить задачу минимизации

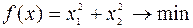, (6.6.6)

при ограничениях

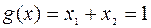. (6.6.7)

Решение. В силу присутствия одного ограничения будет выполнено условие регулярности в виде линейной независимости градиентов ограничений в произвольной точке. Поэтому для поиска подозрительных на минимум точек используем необходимые условия

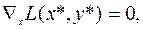
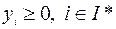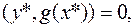, (6.6.8)

для функции Лагранжа, записанной в виде

.

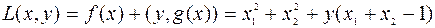В результате получим

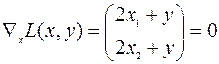
Решая систему уравнений, и исключая 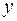, получим взаимосвязь переменных .

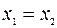На основе условия допустимости, т.е. выполнимости ограничения (6.6.7), с учетом взаимосвязи 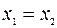, получим 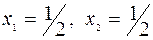, т.е. .

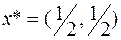Матрица вторых производных функции Лагранжа имеет вид

.

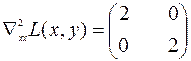В силу неравенства 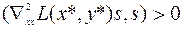для произвольного s и произвольной точки пространства переменных, согласно теореме о достаточных условиях оптимальности, точка 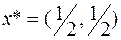является точкой минимума.

Методы нелинейного программированияполучаются из методов минимизации при ограничениях равенствах и неравенствах посредством соответствующих линейных комбинаций.

Глава 7. Основы вариационного исчисления (ВИ)

Постановка задачи, примеры и основные понятия

Вариационное исчисление - математическая дисциплина, посвященная отысканию экстремальных (наибольших или наименьших) значений функционалов. Под функционалом понимается числовая функция, определенная на некоторых классах функций. Функционал ставит в соответствие каждой функции из такого класса некоторое число. Примером функционала является интеграл 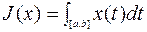, где 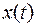- непрерывная функция, определенная на отрезке 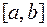. Вариационное исчисление является развитием той части математического анализа, которая посвящена отысканию экстремумов функций.

Пример 1 (задача о брахистохроне). Между точкам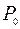и и , расположенными на различной высоте, нужно провести соединяющую их кривую таким образом, чтобы время падения тела, движущегося без трения вдоль кривой из в под действием силы тяжести было минимальным.

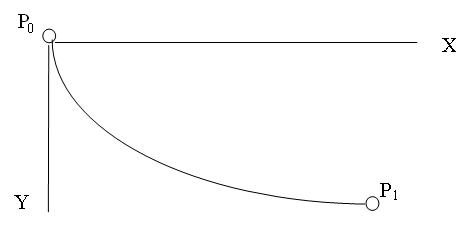
Рис. 1. Задача о брахистохроне

Поместим начало координат в точку 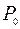и направим оси координат как показано на рис. 1. Предположим, что тело находится в момент начала падения в состоянии покоя. Из закона сохранения энергии следует, что

,

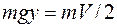откуда для скорости 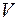имеем 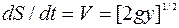, и тем самым время падения 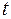(с учетом, что 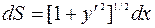) выражается интегралом

.

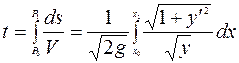Требуется найти функцию 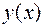, график которой точк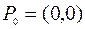и и 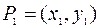, то есть 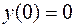и 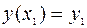, и которая минимизирует указанный интеграл.

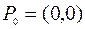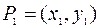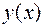Пример 2. Найти кратчайшее расстояние между двумя точками и в плоскости , , т.е. найти функцию , при которой

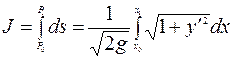
принимает наименьшее значение. При этом 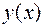должна удовлетворять условиям 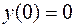и .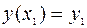

В приведенных примерах отыскиваются функции 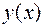, которые минимизируют функционал вида:

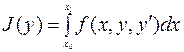(7.1.1)

при граничных условиях:

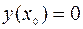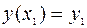, . (7.1.2)

Задача (7.1.1), (7.1.2) - так называемая простейшая задача вариационного исчисления.

Будем рассматривать функции 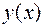из класса непрерывных и непрерывно дифференцируемых функций на 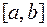, которые будем обозначать 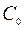и 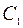соответственно. Определим нормы в 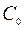и 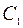. Аналогом расстояния между двумя функциями в каждом из классов является норма разности этих функций. Понятие нормы определяется следующим образом:

в 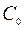: 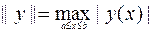; (7.1.3)

в 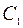: 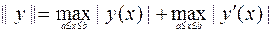. (7.1.4)

В качестве 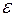–окрестности 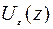функции 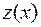понимают тождество

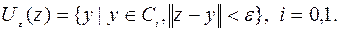(7.1.5)

Если для функции 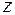из области определения 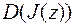существует окрестность 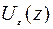такая, что

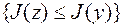или 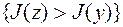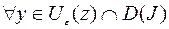, (7.1.6)

то 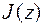называют (локальным) минимумом или максимумом. Элементы из 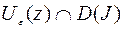называются также функциями сравнения.

Максимум ( минимум ) называется сильным, если в (7.1.6) принята норма на 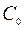. Максимум ( минимум ) называется слабым если в (7.1.6) сравнение кривых происходит в смысле нормы .

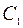Глобальным максимумом ( минимумом ) называют число 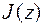для функции 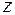, если

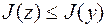
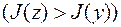
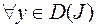. (7.1.7)

Из определения экстремума и норм следует, что сильный экстремум одновременно является слабым.

Основным элементом исследования в ВИ являются понятия первой и второй вариации функционала.

Положим 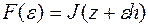и рассмотрим первую и вторую производные функции 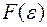по параметру 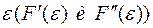при 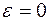. Величины 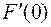и 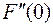называются первой и второй вариацией функционала 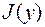и обозначают соответственно 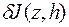и .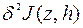

Условия 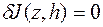и 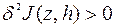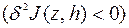могут быть использованы при формулировке необходимых условий экстремума функционала .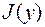