Трапециевидная

Раздел 2. Линейная алгебра

Понятие матрицы. Линейные операции над матрицами

Матрицей размера называется таблица элементов

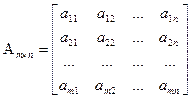. (1)

Матрица (1) имеет строк и 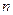столбцов.

Общий элемент матрицы обозначают , где , . Элементы составляют i-ю строку, а элементы – j-й столбец матрицы. Матрицы обозначают большими латинскими буквами . Иногда указывают также размерность матрицы, например .

Виды матриц:

1) прямоугольная матрица ( );

2) квадратная – матрица, у которой число строк равно числу столбцов ( ). При указании размерности возможны обозначения и говорят, что задана квадратная матрица порядка .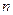

3) треугольная – квадратная матрица, у которой ниже (выше) главной диагонали нули.

-

Верхняя треугольная нижняя треугольная

трапециевидная

.

5) диагональная – квадратная матрица, у которой все элементы, кроме стоящих на главной диагонали, равны нулю:

= diag( ).

6) единичная – диагональная матрица, у которой все элементы (обозначается ), т.е.

.

7) нулевая – матрица, все элементы которой равны нулю. Обозначается О.

.

Понятие равенства определяется только для матриц одинакового размера. Две матрицы 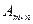и называются равными ( ), если , .

Линейные операции:

1. Умножение матрицы на число: каждый элемент умножаем на число:

.

2. Сложение (вычитание) матриц: складываем (вычитаем) элементы, стоящие на соответствующих местах. Операция определена для матриц одинаковой размерности:

, где , , , т.е.