Корреляция для нелинейной регрессии
НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Поясним понятия аддитивности и линейности, часто отождествляемые. Функция 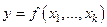 линейна по всем независимым переменным тогда и только тогда, когда
линейна по всем независимым переменным тогда и только тогда, когда 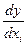 не включает
не включает 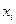 , т.е. когда
, т.е. когда 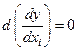 , эффект данного изменения по
, эффект данного изменения по 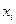 , не зависит от
, не зависит от 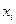 . Мы говорим, что функция
. Мы говорим, что функция 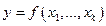 является аддитивной по
является аддитивной по 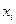 , тогда и только тогда, когда
, тогда и только тогда, когда 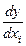 не включает
не включает 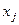
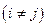 , т.е. тогда, когда
, т.е. тогда, когда 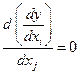 , эффект данного изменения по каждой независимой переменной не зависит от уровня другой переменной. Аддитивность является подходящим определением этой особенности ввиду того, что совместный эффект изменения по всем учтенным независимым переменным может быть получен сложением отдельно вычисленных эффектов изменений по каждой из них. Примеры оценки линейности и аддитивности ряда функций для случая двух объясняющих переменных приведены в таблице.
, эффект данного изменения по каждой независимой переменной не зависит от уровня другой переменной. Аддитивность является подходящим определением этой особенности ввиду того, что совместный эффект изменения по всем учтенным независимым переменным может быть получен сложением отдельно вычисленных эффектов изменений по каждой из них. Примеры оценки линейности и аддитивности ряда функций для случая двух объясняющих переменных приведены в таблице.
Функция 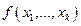 | 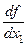 | 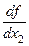 | Линейность | Аддитивность по 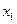 , ,  | |
По 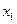 | По  | ||||
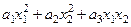 | 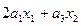 | 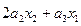 | нет | нет | нет |
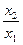 | 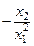 | 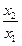 | нет | да | нет |
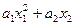 | 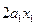 | 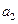 | нет | да | да |
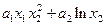 | 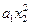 | 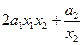 | да | нет | нет |
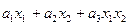 | 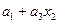 | 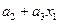 | да | да | нет |
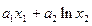 | 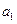 | 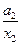 | да | нет | да |
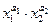 | 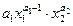 | 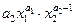 | нет | нет | нет |
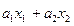 | 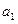 | 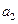 | да | да | да |
Различают два класса нелинейных регрессий:
· регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам (полиномы разных степеней, равносторонняя гипербола);
· регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная).
Второй класс моделей подразделяется на два типа: нелинейные модели, внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть приведена к линейной функции. Более подробно вопрос приведения некоторых нелинейных моделей к линейному виду был рассмотрен на практических занятиях.
В специальных исследованиях по регрессионному анализу часто к нелинейным моделям относят только внутренне нелинейные по оцениваемым параметрам, а все другие, которые внешне нелинейны, но могут быть приведены к линейному виду, относят к классу линейных
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция 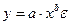 . Связано это с тем, что параметр
. Связано это с тем, что параметр 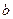 в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента
в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента 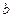 показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Так, если зависимость спроса от цен характеризуется уравнением вида
показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Так, если зависимость спроса от цен характеризуется уравнением вида 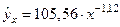 , то, следовательно, с увеличением цен на 1% спрос снижается в среднем на 1,12%. О правомерности подобного истолкования параметра
, то, следовательно, с увеличением цен на 1% спрос снижается в среднем на 1,12%. О правомерности подобного истолкования параметра 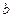 для степенной функции
для степенной функции 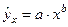 можно судить, если рассмотреть формулу расчета коэффициента эластичности
можно судить, если рассмотреть формулу расчета коэффициента эластичности
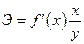 ,
,
где 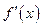 – первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
– первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Для степенной функции она составит 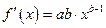 . Соответственно коэффициент эластичности окажется равным:
. Соответственно коэффициент эластичности окажется равным:
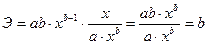
Коэффициент эластичности, естественно, можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру 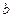 . В других функциях коэффициент эластичности зависит от значений фактора
. В других функциях коэффициент эластичности зависит от значений фактора 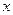 . Так, для линейной регрессии:
. Так, для линейной регрессии:
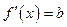 и
и 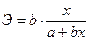 .
.
В силу того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения 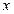 , то обычно рассчитывается средний показатель эластичности по формуле
, то обычно рассчитывается средний показатель эластичности по формуле
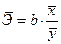 .
.
В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром 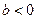 , а эластичность предложения:
, а эластичность предложения: 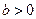 .
.
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли кто будет определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1%. Или, например, на сколько процентов изменится урожайность пшеницы, если качество почвы, измеряемое в баллах, изменится на 1%. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наименьшего значения остаточной вариации), не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита 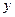 (в процентах годовых) и срока его предоставления
(в процентах годовых) и срока его предоставления 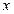 (в днях), было получено уравнение регрессии
(в днях), было получено уравнение регрессии 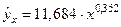 с очень высоким показателем корреляции (0,9895). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция
с очень высоким показателем корреляции (0,9895). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция 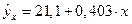 , имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением срока их предоставления на один день.
, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением срока их предоставления на один день.
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Вследствие этого оценка параметров для линеаризуемых функций МНК оказываются несколько смещенной.
КОРРЕЛЯЦИЯ ДЛЯ НЕЛИНЕЙНОЙ РЕГРЕССИИ
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции:
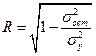
Так как 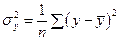 , а
, а 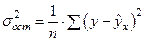 , то индекс корреляции можно выразить так:
, то индекс корреляции можно выразить так:
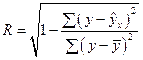
Величина данного показателя находится в пределах 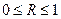 , чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Если нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции.
Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то 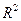 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину
имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину 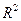 для нелинейных связей называют индексом детерминации.
для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции (см. п. 2.3).
Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по 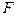 -критерию Фишера:
-критерию Фишера:
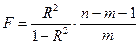
где 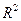 – индекс детерминации;
– индекс детерминации;
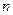 – число наблюдений;
– число наблюдений;
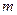 – число параметров при переменных
– число параметров при переменных 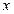 .
.
Величина 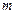 характеризует число степеней свободы для факторной суммы квадратов, а
характеризует число степеней свободы для факторной суммы квадратов, а 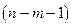 – число степеней свободы для остаточной суммы квадратов.
– число степеней свободы для остаточной суммы квадратов.
Расчет F- критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции.
Индекс детерминации 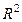 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации 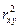 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации 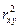 меньше индекса детерминации
меньше индекса детерминации 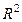 . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина
. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина 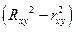 не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия
не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия 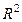 , вычисленных по одним и тем же исходным данным, через
, вычисленных по одним и тем же исходным данным, через 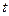 -критерий Стьюдента:
-критерий Стьюдента:
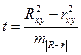
где 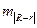 – ошибка разности между
– ошибка разности между 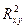
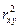 , определяемая по формуле
, определяемая по формуле
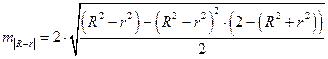
Если 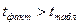 , то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина
, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина 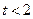 , то различия между
, то различия между 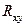 и
и 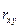 несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
