Методы формализованного описания системы
С учетом замены реальной системы математическим описанием, т.е. системой дифференциальных или разностных уравнений, возникает необходимость для описания поведения системы в любой момент времени.
3.4.1. Математическая модель по “входу-выходу”
Математическая модель считается по “входу-выходу”, если она описывает отображение входных воздействий в выходные и может быть в общем виде представлена уравнениями
Y = A(X, p),
где X, Y – векторы входных и выходных воздействий;
A – некоторый оператор модели, имеет различную природу (может быть оператор свертки, либо некоторая характеристика)
p –вектор параметров модели.
3.4.2. Математическая модель в пространстве состояний
Модели в пространстве состояний – это те, которые описывают не только отображение системой входного сигнала, но и ее внутреннюю структуру.
Для этого удобно использовать единую математическую характеристику – переменную состояния.
Начиная с 60-х годов XX столетия все более популярной становилась форма описания систем управления в пространстве состояний, когда исходные соотношения, описывающие объект управления, представлены в форме Коши, или, что то же самое, в виде системы дифференциальных или разностных уравнений первого порядка.
Состояние системы является основным исходным понятием.
В большинстве практических приложений объекты управления описываются обыкновенными дифференциальными уравнениями или разностными уравнениями разных порядков, которые легко сводятся к системе дифференциальных или разностных уравнений первого порядка
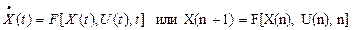 (3.1)
(3.1)
Здесь вектор X характеризует состояние системы, а вектор U описывает внешние воздействия. Через t и n обозначены переменные непрерывного и дискретного времени соответственно. Компонентами вектора состояния X могут быть физические величины.
Вектор X(0) представляет собой минимальный набор величин (x1(0), x2(0),…, xn(0))Т однозначно характеризующий рассматриваемый объект в данный момент времени t0 и позволяющий при известных входных воздействиях U(t), tÎ[t0, tk] получить такой же набор X(t)для любого момента времени в интервале tÎ[t0, tk].
При изменении времени конец вектора состояния описывает в пространстве состояний кривую, называемую траекторией вектора состояния.
Выходные координаты описываемого объекта Y(t), Y(n) могут отличаться от координат вектора состояния и связаны с последним некоторым отображением
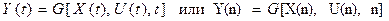 (3.2)
(3.2)
Число выходных координат объекта обычно много меньше размерности вектора состояния. Поэтому описание в пространстве состояний называют внутренним описанием в отличие от внешнего описания в переменных “вход-выход”.
3.4.3. Описание линейных систем в пространстве состояний
Уравнение (3.1) для случая линейной непрерывной системы можно свести к следующим стандартным уравнением состояния
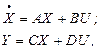 , (3.3)
, (3.3)
где X(t) – вектор состояния системы;
U(t)-вектор управления (входа);
Y(t) - вектор выхода (наблюдения) системы.
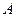 - матрица состояния;
- матрица состояния;
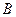 - матрица входа (управления);
- матрица входа (управления);
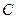 и D- матрицы выходных координат (матрицы наблюдения).
и D- матрицы выходных координат (матрицы наблюдения).
В общем случае размерности векторов и матриц при описании в пространстве состояний таковы:
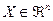 ,
, 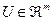 ,
, 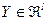 ,
, 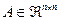 ,
, 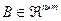 ,
, 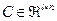
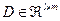 . (3.4)
. (3.4)
Уравнениям (3.3) отвечает структурная схема на рисунке 3.6
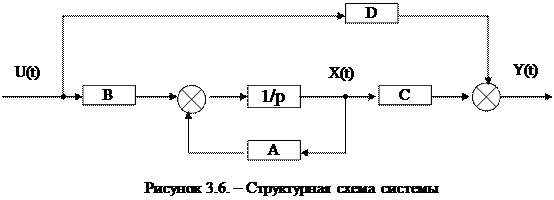
Вместо (3.3) используется также сокращенное обозначение (A, B, C, D).
Матрицы в общем случае A, B, C, D зависят от времени. В этом случае система называется нестационарной.
В стационарных системах A, B, C, D–постоянные, не зависящие от времени матрицы.
Модель (3.3) является одной из распространенных моделей САУ при описании их поведения в пространстве состояний (понятия модель в пространстве состояний и модель в переменных состояния идентичны).
Уравнения состояния дискретных систем принципиально не отличаются от приведенных выше (3.3), в них вместо производных фигурируют конечные разности. Соответствующие уравнения идентичны приведенным выше, в них лишь дифференциалы должны быть заменены на разности.
Пример 1.
Поясним введенные понятия на примере САУ второго порядка с уравнением
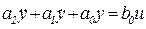 , (3.5)
, (3.5)
где 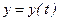 - выходная величина системы,
- выходная величина системы, 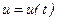 - входное воздействие.
- входное воздействие.
Представим уравнение (3.5) в нормальной форме Коши. С этой целью разрешим его относительно старшей производной выходной величины, что приводит к результату
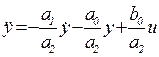 . (3.6)
. (3.6)
Введём некоторый вектор 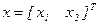 с компонентами
с компонентами 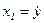 ,
, 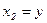 (Т - символ транспонирования). Введем также вектор
(Т - символ транспонирования). Введем также вектор 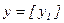 с компонентой
с компонентой 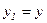 и вектор
и вектор 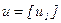 с компонентой
с компонентой 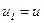 и перепишем уравнение (3.6) с учетом введенных обозначений (при этом
и перепишем уравнение (3.6) с учетом введенных обозначений (при этом 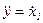 )
)
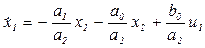 . (3.7)
. (3.7)
Кроме того, очевидно, что 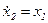 . Таким образом, можно записать систему в форме Коши
. Таким образом, можно записать систему в форме Коши
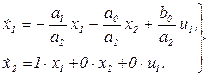 (3.8)
(3.8)
Если ввести матрицы
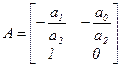 ,
, 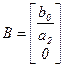 ,
, 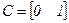 , (3.9)
, (3.9)
то вместо исходного уравнения (3.5) можно записать следующую векторно-матричную модель САУ:
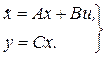 (3.10)
(3.10)
3.4.4. Реализация систем в пространстве состояний
Для одной и той же системы в пространстве состояний можно предложить разные описания (A, B, C, D) в зависимости от того, как выбраны переменные состояния.
При составлении моделей динамических систем в пространстве состояний исходными часто являются описания отдельных звеньев системы в форме дифференциальных уравнений с постоянными коэффициентами.
Рассмотрим составление уравнений состояния для таких звеньев путем приведения их к одному из распространенных видов канонической формы.
Пусть одномерная система задана дифференциальным уравнением порядка n следующего вида:
 (3.11)
(3.11)
которому отвечает передаточная функция

(3.12)
u(t), y(t) – вход и выход системы соответственно;
ai , bj– коэффициенты полиномов, в общем случае функции времени;
i = [1 – n]; j = [1 – m]; m £ n.
Правую часть выражения (3.12) умножим и поделим на pn (pn / pn) и получим:

(3.13)
где
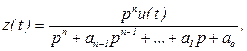 (3.14)
(3.14)
или
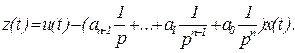 (3.15)
(3.15)
Полученные зависимости (3.13) - (3.15) являются представлением исходного уравнения (3.12) в канонической форме.
 |
Используя эти зависимости, а именно - (3.13) и (3.15) – легко может быть получена эквивалентная структурная схема, моделирующая данную систему, которая представлена на рисунке 3.7. Здесь обозначены соответствующие и переменные состояния X.
Легко проверить, что последней схеме отвечают уравнения состояния
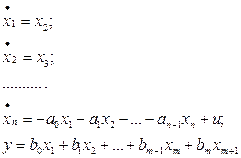 (3.16)
(3.16)
Матрицы A, B, C имеют вид
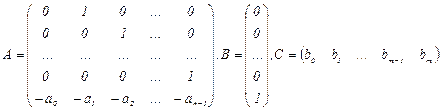 (3.17)
(3.17)
Как следует из рассмотрения (3.16), (3.17), элементы матриц уравнений состояния получаются непосредственно из коэффициентов передаточной функции (3.12).
Приведем примеры использования описанного метода представления дифференциальных уравнений.
Пример 2.
Интегро-дифференцирующее динамическое звено описывается следующим операторным уравнением (первого порядка):
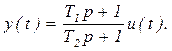 (3.18)
(3.18)
Приведем его к стандартной форме (3.12)
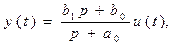 (3.19)
(3.19)
 где
где 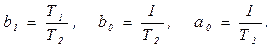
Соответствующая структурная схема, реализующая данное уравнение и получаемая из схемы для общего случая (см. рис. 3.7), имеет вид, представленный на рис. 3.8.
Пример 3.
Дано операторное уравнение второго порядка:
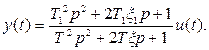 Этим уравнением моделируются динамические характеристики инерционного и форсирующего звеньев второго порядка.
Этим уравнением моделируются динамические характеристики инерционного и форсирующего звеньев второго порядка.
Преобразуя, приведем его к стандартной форме и получим
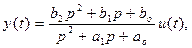
где 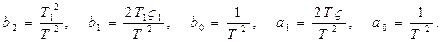
 Соответствующая структурная схема, получаемая из схемы для общего случая (см. рисунок 3.7), имеет вид, представленный на рисунке 3.9.
Соответствующая структурная схема, получаемая из схемы для общего случая (см. рисунок 3.7), имеет вид, представленный на рисунке 3.9.
