Отбор факторов при построении модели множественной регрессии

Теоретически модель множественной регрессии позволяет учесть любое число факторов. Однако на практике ограничиваются наиболее значимыми из них. Предварительный отбор факторов производится на основании опытных данных и теоретических представлений о закономерностях изменения результата Y от значений факторов с учетом следующих требований:

1. Каждый фактор должен быть теоретически обоснованным и количественно измеримым. Если в модель необходимо включить качественный фактор, то ему следует придать количественную определенность (например, экспертная оценка уровня инвестиционной привлекательности региона в баллах).

2. Факторы не должны находиться друг с другом в тесной связи. В противном случае, нельзя достоверно установить, как эти факторы влияют на результат Y по отдельности. Параметры модели, соответствующие тесно связанным факторам, будут неправильно интерпретироваться.

3. В модель целесообразно включать только факторы, оказывающие существенное воздействие на результат Y. Поэтому каждый включаемый фактор должен объяснять вариацию Y. Другими словами, добавление фактора в модель должно увеличивать множественный коэффициент детерминации R². Низкое значение R² означает, что либо в регрессионную модель не включены существенные факторы, либо рассматриваемая форма связи не отражает реального соотношения между переменными.

4. Излишнее насыщение модели факторами не всегда ведет к улучшению ее качества, даже если при этом и увеличивается множественный коэффициент детерминации R². (Вообще говоря, значение R² всегда увеличивается при добавлении новых факторов, хотя это и необязательно означает улучшение модели.) С введением в модель нового фактора должен увеличиваться и скорректированный (нормированный) коэффициент детерминации 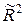, который для линейной модели определяется по формуле

,

(3.9)

где n — число наблюдений; p — число факторов в модели.

В отличие от множественного коэффициента детерминации R² скорректированный коэффициент детерминации 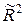уменьшается при включении в модель факторов, не оказывающих ощутимого влияния на результат Y.

На практике существует несколько методов отбора факторов. Наиболее часто применяются три из них:

1. Метод исключения предполагает построение модели, включающей всю совокупность факторов, с последующим сокращением их числа до тех пор, пока не выполнится некоторое, наперед заданное условие. Такими условиями могут быть: наличие в модели только статистически значимых факторов, отсутствие в модели коллинеарных факторов и т.п. Данный метод обычно применяется при большом числе факторов, предположительно влияющих на результат (четыре и более).

2. Метод включения заключается в последовательном включении факторов в модель до тех пор, пока модель не будет отвечать заранее установленному критерию качества, например: наибольшему множественному коэффициенту детерминации, наибольшему скорректированному коэффициенту детерминации, наименьшей средней относительной ошибке аппроксимации и т.п. Последовательность включения факторов в модель определяется с помощью коэффициентов корреляции (парных или частных) между соответствующим фактором и результатом Y: факторы, имеющие больший коэффициент корреляции, включаются в модель первыми.

3. Метод всех возможных регрессий предполагает построение всех возможных регрессионных моделей и выбор лучшей из них по заданному критерию качества, например, наибольшему скорректированному коэффициенту детерминации. Данный метод применяется при малом числе факторов (три и менее), так как при наличии p факторов должно быть построено 2^p моделей. К примеру, при p=5 строится модели!