Устойчивость линейных систем автоматического управления

Основное условие нормального функционирования системы автоматического управления состоит в требовании устойчивости ее переходных процессов. Устойчивость – это свойство системы возвращаться в исходный установившийся режим после выхода из него в результате какого-либо воздействия.

Рассмотрим, от чего зависит устойчивость линейной системы n-го порядка, уравнение движения которой имеет вид:

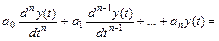
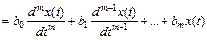, (2.1)

где 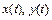– входной и выходной сигналы системы соответственно;

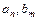– постоянные величины.

Уравнению (2.1) соответствует передаточная функция

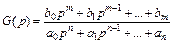. (2.2)

Уравнение, полученное путем приравнивания к нулю выражения в знаменателе передаточной функции (2.2), носит название характеристического уравнения системы:

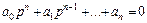. (2.3)

Именно корни 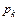характеристического уравнения определяют устойчивость линейной системы в целом. В общем случае они являются комплексными, образуя сопряженные пары

,

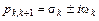где 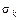– действительная часть корня;

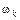– мнимая часть корня;

k – порядковый номер корня.

Переходный процесс в рассматриваемой системе может состоять из колебательных и апериодических составляющих. Каждая колебательная составляющая обязана своим появлением паре комплексных сопряженных корней, а каждая апериодическая – действительному корню.

Независимо от типа корней необходимым и достаточным условиемустойчивости линейной системы является отрицательность действительных частей 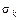всех корней характеристического уравнения системы.

Наличие пары чисто мнимых корней 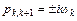соответствует граничному случаю между устойчивостью и неустойчивостью – система при этом находится на границе устойчивости. Такой режим так же не работоспособен, как и неустойчивый.

Необходимым условием устойчивости линейной системы является строгая положительность коэффициентов характеристического уравнения (при условии, что коэффициент 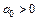, чего всегда можно добиться умножением уравнения на 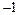). Если хотя бы один из коэффициентов характеристического уравнения будет отрицателен или равен нулю, система однозначно будет являться неустойчивой. Однако положительность всех коэффициентов характеристического уравнения еще не гарантирует устойчивости этой системы. Необходимое условие устойчивости является и достаточным условием только для систем 1-го и 2-го порядков. Уже для систем 3-го порядка оно недостаточно.

Для суждения об устойчивости системы нет необходимости каждый раз находить корни ее характеристического уравнения. Разработаны косвенные признаки, по которым можно судить о знаках действительных частей этих корней, а тем самым и об устойчивости системы, не решая самого характеристического уравнения. Эти признаки называют критериями устойчивости.

Существуют три основных критерия устойчивости: алгебраический критерий Рауса–Гурвица и частотные критерии Найквиста и Михайлова.

2.1 Критерий устойчивости Рауса–Гурвица

По критерию Рауса–Гурвица условия устойчивости линейной системы сводятся к выполнению ряда неравенств, связывающих коэффициенты характеристического уравнения (2.3) рассматриваемой системы 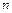-го порядка. Для этого строится матрица Гурвица, содержащая 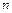строк и 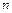столбцов:

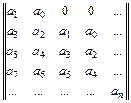. (2.4)

В первый столбец матрицы вписываются все нечетные коэффициенты характеристического уравнения, начиная с a₁, после чего столбец заполняется нулями до положенного числа n элементов. Затем каждая строка матрицы дописывается последовательно коэффициентами с убывающими номерами вплоть до 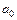, после чего оставшиеся элементы вновь заполняются нулями.

Критерий устойчивости Рауса–Гурвица формулируется следующим образом: для того чтобы рассматриваемая система n-го порядка являлась устойчивой, необходимо и достаточно, чтобы диагональные миноры матрицы Гурвица до 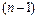-го порядка включительно были строго положительны.

Минор 1-го порядка совпадает с коэффициентом a₁: .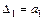

Строгая положительность минора 2-го порядка определяет условие устойчивости системы 3-го порядка:

.

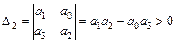Минор 3-го порядка имеет вид:

.

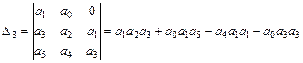Очевидно, что условия устойчивости, вытекающие из критерия Рауса–Гурвица, усложняются с ростом порядка системы. Поэтому данный критерий применяют только для систем невысокого порядка, как правило, не выше четвертого.

Пример 11. Используя критерий Рауса-Гурвица, определить устойчивость системы, характеристическое уравнение которой имеет следующий вид:

.

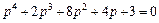Прежде всего проверим выполнение необходимого условия устойчивости. Для этого выпишем коэффициенты характеристического уравнения и проанализируем их:

; ; ; ; .

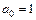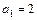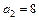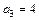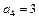Все коэффициенты строго положительны (необходимое условие устойчивости выполнено), однако для системы 4-го порядка этого не достаточно. Строим матрицу Гурвица:

.

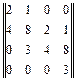Далее проверяем знаки диагональных миноров до 3-го порядка включительно:

,

,

.

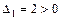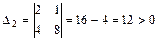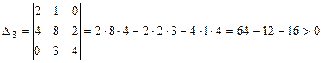Все миноры строго положительны, из чего делаем вывод, что рассматриваемая система устойчива.