Выбор коэффициента охвата k при вычислении расширенной неопределенности
4.10.1 В общем случае коэффициент охвата k выбирают в соответствии с формулой
 , (11)
, (11)
где 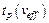 - квантиль распределения Стьюдента с эффективным числом степеней свободы
- квантиль распределения Стьюдента с эффективным числом степеней свободы 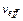 и доверительной вероятностью (уровнем доверия) p. Значения коэффициента
и доверительной вероятностью (уровнем доверия) p. Значения коэффициента 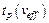 приведены в приложении Г.
приведены в приложении Г.
4.10.2 Эффективное число степеней свободы определяют по формуле
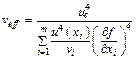 , (12)
, (12)
где 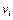 - число степеней свободы при определении оценки i-й входной величины, при этом:
- число степеней свободы при определении оценки i-й входной величины, при этом:
 - для вычисления неопределенностей по типу А;
- для вычисления неопределенностей по типу А;
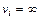 - для вычисления неопределенностей по типу В.
- для вычисления неопределенностей по типу В.
4.10.3 Во многих практических случаях при вычислении неопределенностей результатов измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины и полагают:
k = 2 при 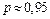 и k = 3 при
и k = 3 при 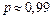 .
.
При предположении о равномерности закона распределения полагают:
k = 1,65 при 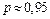 и k = 1,71 при
и k = 1,71 при 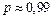 .
.
4.11 При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:
- алгоритм получения результата измерений;
- алгоритм расчета всех поправок и их неопределенностей;
- неопределенности всех используемых данных и способы их получения;
- алгоритмы вычисления суммарной и расширенной неопределенностей (включая значение коэффициента k).
5 Соответствие между формами представления результатов измерений, используемыми в НД ГСИ по метрологии, и формой, используемой в Руководстве
5.1 При проведении совместных работ с зарубежными странами в работах, проводимых под эгидой МКМВ и его Консультативных комитетов, при подготовке публикаций в зарубежной печати, при публикациях работ по определению физических констант и в других случаях, связанных с выполнением международных метрологических работ, целесообразно руководствоваться нижеприведенными схемами.
5.1.1 При вычислении неопределенности измерений следует придерживаться последовательности, показанной на рисунке 1.
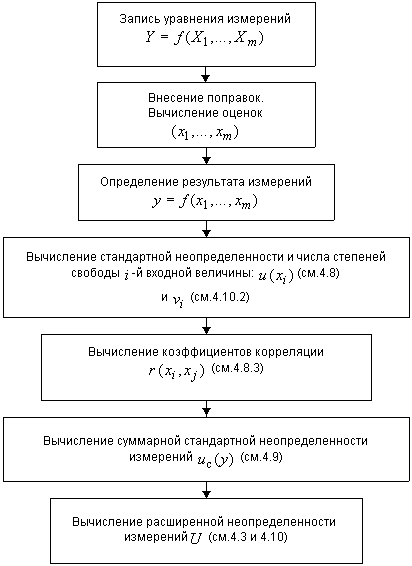
Рисунок 1
5.2 Сопоставление способов оценивания доверительных границ погрешности  и вычисления расширенной неопределенности
и вычисления расширенной неопределенности 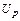 измерений приведено в таблице 1.
измерений приведено в таблице 1.
Таблица 1
| НД ГСИ по метрологии |  | 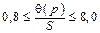 |  |
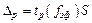 , , | 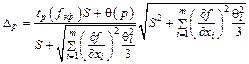 , , | 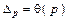 | |
где  ; ; 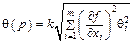 , здесь k = 1,1 при p = 0,95 и k =1,4 при p =0,99 и m >4 , здесь k = 1,1 при p = 0,95 и k =1,4 при p =0,99 и m >4 | |||
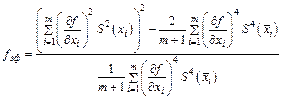 | |||
| Руководство |  , где , где 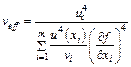 , причем , причем  - для неопределенностей, вычисленных по типу А; - для неопределенностей, вычисленных по типу А; 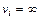 - для неопределенностей, вычисленных по типу В - для неопределенностей, вычисленных по типу В | ||
| Для большинства практических случаев в предположении: - нормального закона распределения U0,95 = ni - 1, U0,99 = 3uc; - равномерного закона распределения U0,95 = 1,65uc, U0,99 = 1,71 uc |
5.3 При сопоставлении оценок характеристик погрешности и неопределенностей результатов измерений рекомендуется использовать следующую схему (с учетом пояснений А..5 и А.6 приложения А):
| СКО, характеризующее случайную погрешность |  | Стандартная неопределенность, вычисленная по типу А |
| СКО, характеризующее неисключенную систематическую погрешность |  | Стандартная неопределенность, вычисленная по типу В |
| СКО, характеризующее суммарную погрешность |  | Суммарная стандартная неопределенность |
| Доверительные границы погрешности |  | Расширенная неопределенность |
5.4 Если отсутствует достаточная информация для вычисления неопределенности u в соответствии с Руководством (раздел 4 настоящей рекомендации), то ее оценка 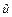 может быть получена на основании оценок характеристик погрешности по приведенным ниже схемам. Схемы 1 и 2 соответствуют двум различным способам представления результатов измерений, принятым в НД ГСИ по метрологии. Необходимо отметить, что оценки неопределенностей, полученные таким образом, в ряде случаев не совпадают со значениями неопределенностей, полученными в соответствии с Руководством (см. приложение В).
может быть получена на основании оценок характеристик погрешности по приведенным ниже схемам. Схемы 1 и 2 соответствуют двум различным способам представления результатов измерений, принятым в НД ГСИ по метрологии. Необходимо отметить, что оценки неопределенностей, полученные таким образом, в ряде случаев не совпадают со значениями неопределенностей, полученными в соответствии с Руководством (см. приложение В).
Схема 1
| y – результат измерений; S – СКО случайной погрешности; q(p) - доверительные границы неисключенной систематической погрешности результата измерений; m – число входных величин; fэф - оценка эффективного числа степеней свободы, fэф = n -1 -при прямых измерениях (где n – число измерений) |  | y = результат измерений; 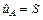 - оценка стандартной неопределенности, вычисленной по типу А; - оценка стандартной неопределенности, вычисленной по типу А;  - оценка стандартной неопределенности, вычисленной по типу В, при этом: k = 1,1 - при p = 0,95 и k = 1,4 - при p = 0,99и m > 4; - оценка стандартной неопределенности, вычисленной по типу В, при этом: k = 1,1 - при p = 0,95 и k = 1,4 - при p = 0,99и m > 4;  - оценка суммарной стандартной неопределенности; - оценка суммарной стандартной неопределенности;  - оценка эффективного числа степеней свободы; - оценка эффективного числа степеней свободы;  - оценка расширенной неопределенности - оценка расширенной неопределенности | |
Схема 2
y – результат измерений; 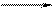 Dp - доверительные границы погрешности измерений; p – доверительная вероятность Dp - доверительные границы погрешности измерений; p – доверительная вероятность | y – результат измерений; 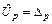 - оценка расширенной неопределенности; - оценка расширенной неопределенности;  - оценка суммарной стандартной неопределенности; - оценка суммарной стандартной неопределенности; 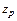 - квантиль нормального распределения - квантиль нормального распределения | |
Оценить неопределенности uA и uB по отдельности, зная толькоDp, невозможно.
ПРИЛОЖЕНИЕ А
(справочное)
Сравнительный анализ двух подходов к выражению характеристик точности измерений
A.1 Целью измерений является получение оценки истинного значения измеряемой величины. Понятие погрешности измерений как разности между результатом измерений и истинным (действительным) значением измеряемой величины используется для описания точности измерений в НД ГСИ по метрологии. Говоря об оценивании погрешности, в метрологической практике государств - участников Соглашения подразумевают оценивание ее характеристик.
| Погрешность |  | Характеристика погрешности |  |  Алгоритм оценивания Алгоритм оценивания | Оценка характеристики погрешности |
А.2 В Руководстве для выражения точности измерений вводят понятие неопределенности измерений. Неопределенность измерений понимают как неполное знание значения измеряемой величины и для количественного выражения этой неполноты вводят распределение вероятностей возможных (обоснованно приписанных) значений измеряемой величины. Таким образом, параметр этого распределения (также называемый - неопределенность) количественно характеризует точность результата измерений.
А.3 Сходными для обоих подходов являются последовательности действий при оценивании характеристик погрешности и вычислении неопределенности измерений:
- анализ уравнения измерений;
- выявление всех источников погрешности (неопределенности) измерений и их количественное оценивание;
- введение поправок на систематические погрешности (эффекты), которые можно исключить.
А.4 Методы вычисления неопределенности, так же как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайных величин. Кроме изложенных в Руководстве и НД ГСИ по метрологии методов вычисления неопределенности и оценивания характеристик погрешности на практике используют и другие методы.
Возможные различия между оценками характеристик погрешности (в соответствии с НД ГСИ по метрологии) и неопределенностями (в соответствии с Руководством) показаны в примерах, приведенных в приложениях Б и В.
Различие двух подходов проявляется также в трактовке неопределенности и характеристик погрешности, основанной на разных интерпретациях вероятности: частотной и субъективной. В частности, доверительные границы погрешности (откладываемые от результата измерений) накрывают истинное значение измеряемой величины с заданной доверительной вероятностью (частотная интерпретация вероятности). В то же время аналогичный интервал  трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине (субъективная интерпретация вероятности).
трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине (субъективная интерпретация вероятности).
А.5 В общем случае не существует однозначного соответствия между случайными погрешностями и неопределенностями, вычисленными по типу А (а также неисключенными систематическими погрешностями и неопределенностями, вычисленными по типу В). Деление на систематические и случайные погрешности обусловлено природой их возникновения и проявления в ходе измерительного эксперимента, а деление на неопределенности, вычисляемые по типу А и по типу В, - методами их расчета.
А.6 Результаты сравнительного анализа процедур оценивания характеристик погрешности и вычисления неопределенности измерений приведены в таблицах A.1 и А.2.
Таблица A.1 - Процедура оценивания характеристик погрешности результата измерений
| Погрешность | x = y - yист Û y = yист + x | |||
| Модель погрешности | x- случайная величина с плотностью распределения вероятностей p(x; E, s2, …) где E - математическое ожидание, s2 - дисперсия | |||
| Характеристики погрешности | S- СКО | q - границы неисключенной систематической погрешности | Dp - доверительные границы | |
| Исходные данные для оценивания характеристик погрешности | 1 Модель объекта исследования. 2 Экспериментальные данные xiq, где q = 1, ni; i = 1, …, m 3 Информация о законах распределения. 4 Сведения об источниках погрешностей, их природе и характеристиках составляющих [S(xi), qi], структурная модель погрешности. 5 Стандартные справочные данные и другие справочные материалы | |||
| Методы оценивания характеристик: 1 случайных погрешностей |  ; ;  ; ;  | |||
| 2 неисключенных систематических погрешностей | 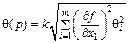 , где k = 1,1 при p = 0,95 и k = 1,4 при p = 0,99 и m > 4 , где k = 1,1 при p = 0,95 и k = 1,4 при p = 0,99 и m > 4 | |||
| 3 суммарной погрешности |  | |||
| Форма представления характеристик погрешности | q(p), S, n, fэф | Dp | ||
| Интерпретация полученных результатов | Интервал (-Dp, +Dp с вероятностью p содержит погрешность измерений, что равносильно тому, что интервал (y - Dp, y + Dp) с вероятностью p содержит истинное значение измеряемой величины. | |||
Таблица А.2 - Процедура вычисления неопределенности измерений
| Модель неопределенности (представление знания о значении измеряемой величины) | h - случайная величина с плотностью распределения вероятностей p (x,y,u2, …), где y - математическое ожидание, u2 - дисперсия | ||
| Неопределенность (количественная мера) | Стандартная u | Суммарная    | Расширенная Up = k × uc |
| Исходные данные для вычисления неопределенности | 1 Модель объекта исследования. 2 Экспериментальные данные xiq, где q = 1; …, ni; i = 1, …, m. 3 Информация о законах распределения. 4 Сведения об источниках неопределенности и информация о значениях неопределенности. 5 Стандартные справочные данные и другие справочные материалы | ||
| Методы вычисления неопределенности: | |||
| 1 по типу А |  ; ;  | ||
| 2 по типу В |  UB(xi) = UB(xi) =  | ||
| 3 расширенной неопределенности | Up = tp(veff)×uc, где  ; ; 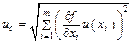 ; U0,95 = 2uc, U0,99 = 3uc - для нормального закона; U0,95 = 1,65uc, U0,99 = 1,17uc - для равномерного закона ; U0,95 = 2uc, U0,99 = 3uc - для нормального закона; U0,95 = 1,65uc, U0,99 = 1,17uc - для равномерного закона | ||
| Представление неопределенности | Uc, up, k, ui, vi | ||
| Интерпретация полученных результатов | Интервал (y – Up, y + Up) содержит большую долю (p) распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине. |
ПРИЛОЖЕНИЕ Б
(справочное)
Пример оценивания характеристик погрешности и вычисления неопределенности измерений. Измерения силы электрического тока с помощью вольтметра и токового шунта
