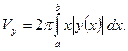Интегрирование некоторых иррациональных выражений
ИНТЕГРАЛЫ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
для самостоятельной работы студентов 1 – 2 курсов
всех специальностей заочной и дистанционной формы обучения
ШАХТЫ 2003
УДК 517 (075.8)
БК 22.16 я 73
И 73
Составители:
к.ф.-м.н., доцент кафедры «Математика»
А.Б. Михайлов
к.т.н., доцент кафедры «Математика»
Г.Р. Саакян
ст. преподаватель кафедры «Математика»
Михайлова И.Д.
Рецензенты:
к.т.н., доцент кафедры «Математика»
Г.В. Филькин
к.т.н., доцент кафедры «Математика»
Син Л.И.
И 73 Михайлов А.Б. Интегралы: Пособие/ А.Б. Михайлов, Г.Р. Саакян, И.Д. Михайлова. – Шахты: Изд-во ЮРГУЭС, 2003. – 25 с.
Пособие предназначено для студентов заочной и дистанционной форм обучения всех специальностей. Оно содержит краткий теоретический материал и большое количество разнообразных примеров по теме «Интегральное исчисление функций». Пособие призвано помочь студентам подготовиться к выполнению аудиторной контрольной работы и сдаче экзамена.
УДК 517 (075.8)
БК 22.16 я 73
© Южно-Российский государственный
университет экономики и сервиса, 2003
© А.Б. Михайлов, Г.Р. Саакян, И.Д. Михайлова
СОДЕРЖАНИЕ
1. Справочный материал ……………………………………………....4
2. Примеры выполнения практических заданий …………………….11
3. Задачи для самостоятельного решения …………………………….17
Ответы к задачам для самостоятельного решения ………………..19
Библиографический список …………………………………………20
СПРАВОЧНЫЙ МАТЕРИАЛ
1.1 Первообразная и неопределенный интеграл. Пусть Т – некоторый промежуток на числовой оси, на котором заданы функции f(x) и F(x).
Определение. Функция F(x) называется первообразной функции f(x) на промежутке Т, если 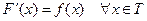 .
.
Определение. Пусть функция f задана на промежутке Т. Совокупность всех ее первообразных на этом промежутке называется неопределенным интегралом от функции f и обозначается
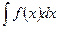 .
.
Если F(x) – какая-либо первообразная функция f на рассматриваемом промежутке, то
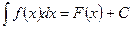 ,
,
где С – произвольная постоянная.
Основные свойства неопределенного интеграла
1) Если функция F(x) дифференцируема на промежутке Т, то
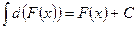 .
.
2) Пусть функция f(x) имеет первообразную на промежутке Т, тогда справедливо равенство
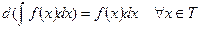 .
.
3) Если функция 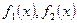 имеют первообразные на промежутке Т, то для любых
имеют первообразные на промежутке Т, то для любых 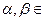 R функция
R функция 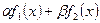 имеет первообразную на этом промежутке, причем
имеет первообразную на этом промежутке, причем
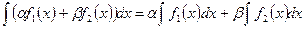 .
.
Таблица интегралов
1) 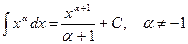 .
.
2) 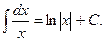
3) 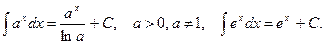
4) 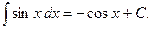
5) 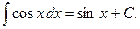
6) 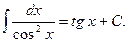
7) 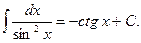
8) 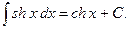
9) 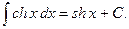
10) 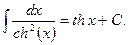
11) 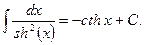
12) 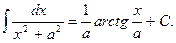
13) 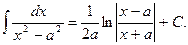
14) 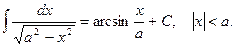
15) 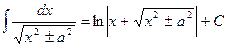
(если под корнем 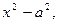 то
то 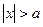 ).
).
1.4 Формула замены переменной. Пусть функции 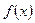 и
и 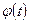 определены соответственно на промежутках Т и Т1 , причем
определены соответственно на промежутках Т и Т1 , причем 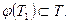 Если функция f имеет на Т первообразную F(x) и, следовательно,
Если функция f имеет на Т первообразную F(x) и, следовательно,
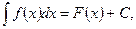
а функция 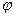 дифференцируема на Т1, то функция
дифференцируема на Т1, то функция 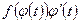 имеет на Т1 первообразную
имеет на Т1 первообразную 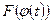 и
и
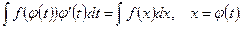 (1)
(1)
Иначе говоря, сделаем сначала подстановку 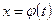 , а затем возьмем интеграл, или сначала возьмем интеграл, а потом сделаем указанную подстановку, - результат будет один и тот же.
, а затем возьмем интеграл, или сначала возьмем интеграл, а потом сделаем указанную подстановку, - результат будет один и тот же.
Отметим, что формулу (1) бывает целесообразно использовать и в обратном порядке, т.е. справа налево. Именно, иногда удобно вычисление интеграла 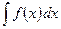 с помощью соответствующей замены переменного
с помощью соответствующей замены переменного 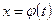 свести к вычислению интеграла
свести к вычислению интеграла
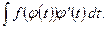
В случае, когда функция 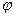 имеет обратную
имеет обратную 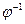 , то воспользовавшись формулой (1) справа налево, сводим вычисление
, то воспользовавшись формулой (1) справа налево, сводим вычисление 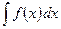 к вычислению
к вычислению 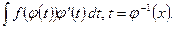 Эта формула называется обычно формулой интегрирования заменой переменного.
Эта формула называется обычно формулой интегрирования заменой переменного.
1.5 Формула интегрирования по частям. Если функции u(x), v(x) дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл 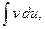 то на нем существует и интеграл
то на нем существует и интеграл 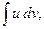 причем
причем
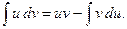
Эта формула называется формулой интегрирования по частям. Дадим некоторые рекомендации для использования этой формулы. А именно, что целесообразно обозначить под интегралом через функцию u, а что брать в качестве дифференциала dv. Пусть Р(х) – некоторый многочлен. Тогда
1) 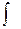
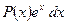
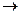
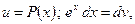
2) 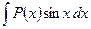
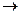
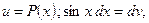
3) 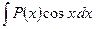
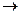
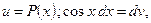
4) 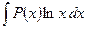
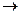
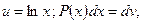
5) 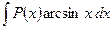
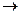
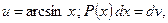
6) 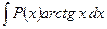
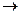
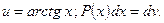
Отметим, что при необходимости формулу интегрирования по частям можно применять несколько раз подряд.
1.6 Интегрирование рациональных дробей. Рассмотрим интеграл 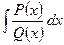 от рациональной функции. Метод нахождения таких интегралов основан на возможности разложения любой правильной рациональной дроби на сумму элементарных дробей. К элементарным относятся дроби вида
от рациональной функции. Метод нахождения таких интегралов основан на возможности разложения любой правильной рациональной дроби на сумму элементарных дробей. К элементарным относятся дроби вида
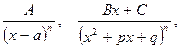
где n – некоторое натуральное число, а трехчлен 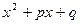 не имеет действительных корней.
не имеет действительных корней.
Остановимся подробнее на этапах этого метода.
1) Если дробь 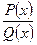 неправильная, то поделив числитель на знаменатель, выделим целую часть
неправильная, то поделив числитель на знаменатель, выделим целую часть
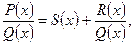
при этом степень многочлена 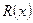 меньше степени многочлена
меньше степени многочлена 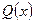 .
.
2) Разложим знаменатель 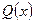 на множители
на множители 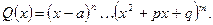
3) Представим правильную дробь 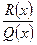 в виде суммы элементарных дробей
в виде суммы элементарных дробей
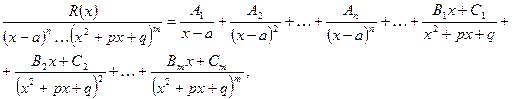
где коэффициенты 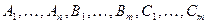 пока не определены.
пока не определены.
4) Находим в последнем разложении неизвестные коэффициенты и сводим тем самым интеграл 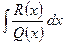 к вычислению суммы интегралов от элементарных дробей.
к вычислению суммы интегралов от элементарных дробей.
1.7 Интегралы вида 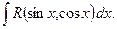
а) В общем случае интегралы вида 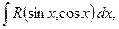 где
где 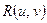 - рациональная функция двух переменных, сводятся к интегралу от рациональной функции одной переменной путем универсальной тригонометрической подставки
- рациональная функция двух переменных, сводятся к интегралу от рациональной функции одной переменной путем универсальной тригонометрической подставки 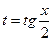 ,
, 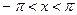 . Действительно,
. Действительно,
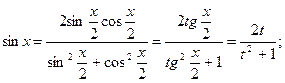
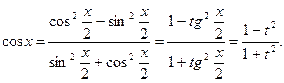
Из равенства 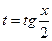 следует, что
следует, что 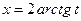 и
и 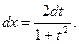
Тогда
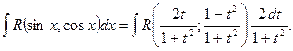
б) Если подынтегральная функция имеет вид 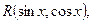 но
но 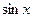 и
и 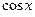 входят только в четных степенях (допускается наличие произведения
входят только в четных степенях (допускается наличие произведения 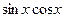 ), то удобно применять подстановку
), то удобно применять подстановку 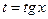 или
или 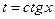 .
.
В этом случае
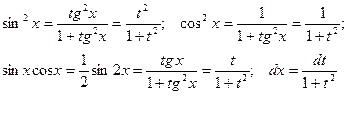 .
.
в) Интегралы 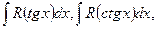 где
где 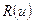 - рациональная функция, сводятся к интегралу от рациональной функции переменной
- рациональная функция, сводятся к интегралу от рациональной функции переменной 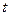 заменой
заменой 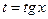 или
или 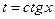 :
:
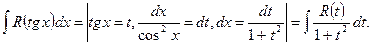
1.8 Интегралы вида 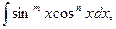 где
где 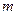 и
и 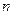 - целые числа
- целые числа
а) Пусть хотя бы одно из целых чисел 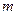 или
или 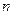 - нечетное, например,
- нечетное, например, 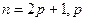 - некоторое целое число. Тогда
- некоторое целое число. Тогда
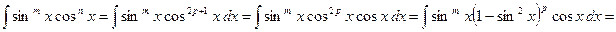
= 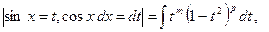
и исходный интеграл сводится к интегралу от рациональной функции.
б) Пусть 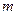 и
и 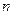 - четные неотрицательные целые числа. Тогда интеграл
- четные неотрицательные целые числа. Тогда интеграл 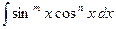 вычисляют с использованием тригонометрических формул понижения степени:
вычисляют с использованием тригонометрических формул понижения степени:
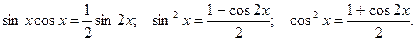
Интегралы вида
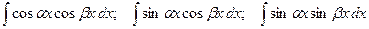
вычисляются при помощи формул:
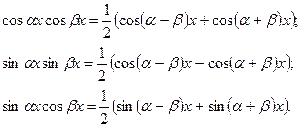
Интегрирование некоторых иррациональных выражений
а) Рассмотрим интегралы вида
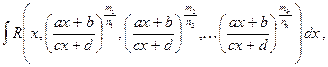 (2)
(2)
где R – рациональная функция от 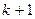 переменных,
переменных, 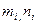 - натуральные числа,
- натуральные числа, 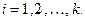
Пусть S – наименьший общий знаменатель дробей 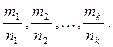 Тогда с помощью замены
Тогда с помощью замены 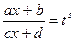 интеграл (2) сводится к интегралу от рациональной функции переменного
интеграл (2) сводится к интегралу от рациональной функции переменного 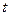 .
.
Рассмотрим, например, интеграл
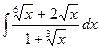 .
.
Выбирая наименьший общий знаменатель дробей 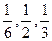 (то есть 6), сделаем замену
(то есть 6), сделаем замену 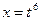 . Тогда
. Тогда 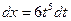 и
и
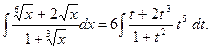
Остается вычислить последний интеграл, как это указано в 1.6.
б) При вычислении интегралов вида
1) 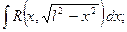 2)
2) 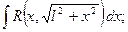 3)
3) 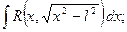
где 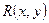 - рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
- рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
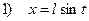 или
или 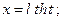 2)
2) 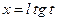 или
или 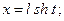 3)
3) 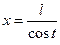 или
или 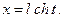
В этом случае исходные интегралы сводятся к интегралам, описанным в 1.7 и в 1.8.
в) Интегралы от дифференциального бинома, т.е. интегралы вида
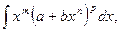
где 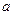 и
и 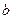 - действительные числа, а
- действительные числа, а 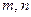 и
и 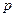 - рациональные, сводятся к интегралу от обычной рациональной функции одного переменного только в трех случаях (теорема Чебышева):
- рациональные, сводятся к интегралу от обычной рациональной функции одного переменного только в трех случаях (теорема Чебышева):
1) 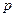 -целое число; 2)
-целое число; 2) 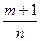 - целое число; 3)
- целое число; 3) 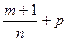 - целое число.
- целое число.
В первом случае это делается при помощи подстановки 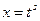 , где s – общий знаменатель дробей
, где s – общий знаменатель дробей 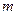 и
и 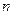 ; во втором случае можно положить
; во втором случае можно положить 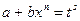 , где s – знаменатель дроби
, где s – знаменатель дроби 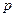 ; в третьем применяют подстановку
; в третьем применяют подстановку 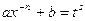 , где s – знаменатель дроби
, где s – знаменатель дроби 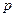 .
.
1.11 Определенный интеграл. Понятие определенного интеграла Римана и его свойства хорошо изложены в литературе (см. /1 – 4/), поэтому мы останавливаться на этом не будем. Рассмотрим лишь способы вычисления определенных интегралов и их приложения.
а) Формула Ньютона-Лейбница (основная теорема интегрального исчисления).
Пусть функция 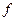 непрерывна на отрезке
непрерывна на отрезке 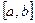 . Если функция
. Если функция 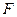 является произвольной ее первообразной на этом отрезке, то
является произвольной ее первообразной на этом отрезке, то
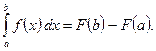
б) Формула замены переменной.
Пусть
1) функция 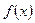 непрерывна на отрезке
непрерывна на отрезке 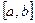 ;
;
2) функция 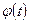 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 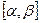 , причем
, причем 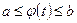 для всех
для всех 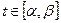 , и
, и 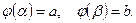
Тогда
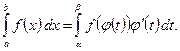
Таким образом, при замене переменного 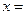
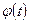 в определенном интеграле
в определенном интеграле 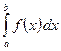 следует всюду формально заменить
следует всюду формально заменить 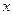 на
на 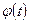 и соответственно изменить пределы интегрирования.
и соответственно изменить пределы интегрирования.
в) Формула интегрирования по частям.
Если функции 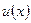 и
и 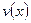 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 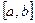 , то
, то
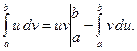
Вычисление площадей
а) Если функция 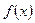 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке 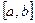 , то площадь S криволинейной трапеции, ограниченной линиями
, то площадь S криволинейной трапеции, ограниченной линиями 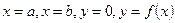 , вычисляется по формуле
, вычисляется по формуле
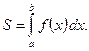
б) Если 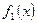 и
и 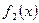 непрерывные на отрезке
непрерывные на отрезке 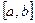 функции, причем
функции, причем 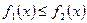 на этом отрезке, то площадь фигуры, ограниченной линиями
на этом отрезке, то площадь фигуры, ограниченной линиями 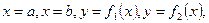 вычисляется по формуле
вычисляется по формуле
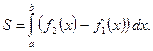
в) Если непрерывная кривая 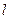 задана параметрическими уравнениями
задана параметрическими уравнениями 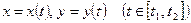 , причем
, причем 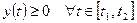 , то площадь криволинейной трапеции, ограниченной этой кривой и прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой и прямыми 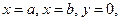 выражается формулой
выражается формулой
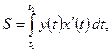
где 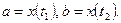
г) Площадь сектора AOB, ограниченного непрерывной кривой 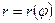 (заданной в полярных координатах) и двумя лучами
(заданной в полярных координатах) и двумя лучами 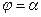 и
и 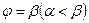 , равна
, равна
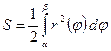 .
.
Вычисление длин дуг.
а) Длина дуги гладкой (непрерывно дифференцируемой) кривой 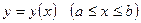 равна
равна
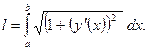
б) Если кривая С задана параметрическими уравнениями 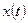 и
и 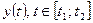 , где
, где 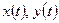 - непрерывно дифференцируемые на отрезке
- непрерывно дифференцируемые на отрезке 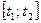 , то длина дуги кривой С выражается формулой
, то длина дуги кривой С выражается формулой
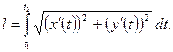
в) Если кривая С задана в полярных координатах уравнением 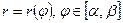 , где
, где 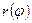 - непрерывно дифференцируемая на отрезке функция, то длина дуги соответствующей кривой равна
- непрерывно дифференцируемая на отрезке функция, то длина дуги соответствующей кривой равна
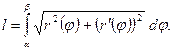
Вычисление объемов
а) Если объем тела существует и 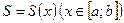 есть площадь сечения тела плоскостью, перпендикулярной оси Ox в точке x, то
есть площадь сечения тела плоскостью, перпендикулярной оси Ox в точке x, то
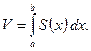
б) Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции
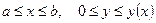 ,
,
где 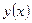 - непрерывная функция, равен
- непрерывная функция, равен
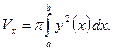
В более общем случае, объем кольца, образованного вращением вокруг оси Ox фигуры 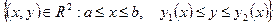 , где
, где 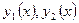 - непрерывные неотрицательные функции, равен
- непрерывные неотрицательные функции, равен
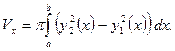
Объем тела, образованного вращением вокруг оси Oy плоской фигуры
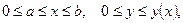
где 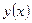 - непрерывная функция, равен
- непрерывная функция, равен