Математическая модель внешней среды

Движущиеся в атмосфере ЛА и НАСП испытывают, в том числе, действие аэродинамической силы. Величина и направление аэродинамической силы и ее момента зависят от параметров атмосферы. Ниже приведены основные характеристики атмосферы.

Атмосферу разделяют на четыре слоя: тропосферу, стратосферу, ионосферу и экзосферу. В основе приведенного выше деления атмосферы лежит прежде всего механизм регулирования температуры воздуха. Тепловое равновесие атмосферы определяется поглощением ультрафиолетового излучения Солнца ее верхними слоями, поглощением (вблизи поверхности Земли) теплового излучения земли парами воды и углекислым газом и излучением принятой энергии. Поглощение теплового излучения Земли нижним слоем атмосферы вызывает конвекционное перемешивание воздуха в тропосфере. Вследствие малой теплопроводности воздуха в тропосфере создаются условия для адиабатического равновесия. В отличие от тропосферы в верхних слоях атмосферы распределение температуры с высотой определяется не конвекцией, а излучением.

Исследования показали, что физические параметры атмосферы значительно изменяются в зависимости от климатических условий, времени года и высоты. Например, в слое атмосферы с высотой до 5000 м содержится около 50% всей массы воздуха, а с высотой до 20 000 м – около 95%.

Стандартная атмосфера – это макет атмосферы, полученной осреднением параметров реальной атмосферы по временам года и координатам точки земной поверхности. Отклонение метеоусловий от их нормальных значений учитывается отдельно в теории поправок.

До 1920 г. в нашей стране пользовались условной атмосферой, полученной путем обработки приземных метеорологических условий в районе Москвы. В 1920 г. была принята международная стандартная атмосфера (МСА). Для артиллерийской практики в 1927 г. ввели нормальную артиллерийскую атмосферу (НАА), которая определяется следующими параметрами у Земли:

R = 287 Дж/кг × град;

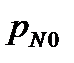= 10⁵ Н/м²;

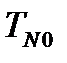= 288,9° (К).

В 1949 г. были опубликованы подробные таблицы стандартной атмосферы (ГОСТ 4401-48). С развитием авиации и ракетной техники возникла необходимость, и появились технические возможности исследования верхних слоев атмосферы. К концу 1950-х гг. был накоплен большой экспериментальный материал, который позволил координационному комитету АН СССР выступить с проектом новой стандартной атмосферы. Сначала была принята временная стандартная атмосфера ВСА-60, а позже стандартная атмосфера СА-64. В настоящее время в теории воздушной стрельбы и бомбометании в соответствии с ГОСТ 4401-81 действует СА-81.

Стандартная атмосфера предназначается, в том числе, для использования при расчетах и проектировании ЛА, составления баллистических таблиц бомбометания и воздушной стрельбы, а также для приведения результатов испытаний БАК и их элементов к одинаковым условиям. В СА-81 установлены стандартные численные значения параметров атмосферы в функции геометрической h и геопотенциальной H высот в диапазоне от –2 000 до 50 000 м.

В СА-81 g(h) вычисляется без учета центробежного ускорения по формуле для сферической модели Земли [15]:

,

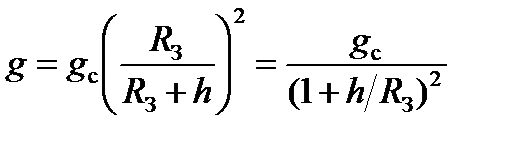где g_c = 9,80665 м/с² – стандартное ускорение свободного падения на среднем уровне моря;

R_З = 6 356 767 м – условный радиус Земли.

Уравнение состояния для идеального газа:

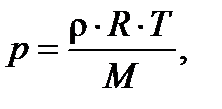
где R – универсальная газовая постоянная;

M – молярная масса воздуха.

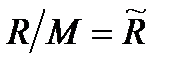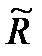Для высот до 94 км значение молярной массы остается постоянным, и отношение , где – удельная газовая постоянная. Тогда:

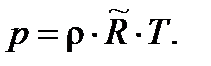
В зависимости от характера изменения температуры атмосфера СА-81 по высоте разбита на ряд слоев; температура в каждом слое аппроксимируется линейной функцией геопотенциальной высоты:

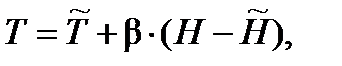
где 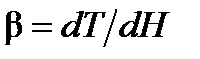– градиент температуры по геопотенциальной высоте;

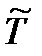и 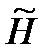– температура и геопотенциальная высота нижней границы соответствующего слоя.

Для изотермических слоев (β = 0):

.

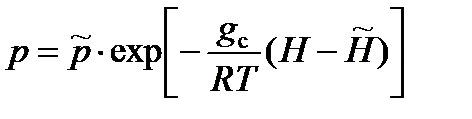Для слоев с линейно изменяющейся температурой (β ≠ 0):

.

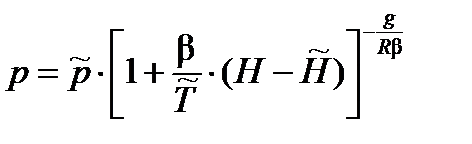Плотность определяется из уравнения состояния:

.

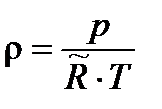Скорость звука:

,

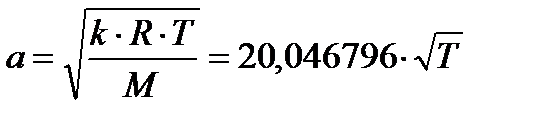где 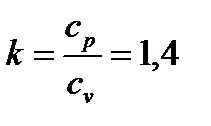– показатель адиабаты.