Движение с переменной скоростью.
Кинематика (5 занятий)
Движение с постоянной скоростью.
Задача 1
Радиолокатор определяет координаты летящего самолета, измеряя угол между направлением на Северный Полюс и направлением на самолет и расстояние от радиолокатора до самолета. В некоторый момент времени положение самолета определялось координатами α1 = 44°, расстояние R1 = 100 км. Через промежуток времени равный 5 с после этого момента координаты самолета были: α2 = 46°, расстояние R2 = 100 км. Изобразите в декартовой системе координат с осью у, направленной на север, и с радиолокатором в начале координат положение самолета в оба момента времени; определите модуль и направление его скорости. Угол отсчитывайте по часовой стрелке.
Задача 2
Три микрофона, расположенные на одной прямой в точках А, В, С, последовательно зарегистрировали сигнал в моменты времени tA > tB > tC звук от взрыва, который произошел в точке O, лежащей на отрезке АС. Найдите длину отрезка АО, если АВ = ВС = L. В какой момент времени произошел взрыв?
Задача 3
С подводной лодки, погружающейся вертикально и равномерно, испускаются звуковые сигналы длительности t0. Длительность приема отраженного от дна импульса составляет t. Скорость звука в воде равна с. С какой скоростью погружается подводная лодка?
Задача 4
Из взрывчатого вещества изготовлен стержень длины l. Скорость детонации (скорость вовлечения во взрыв новых участков взрывчатого вещества) равна v, а скорость разлета продуктов взрыва u <v. Как изменяется со временем область занятая продуктами взрыва, если стержень подрывается с одного из концов?
Задача 5
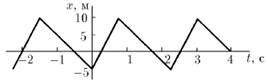
По графику зависимости координаты от времени постройте график зависимости скорости от времени.
Задача 6
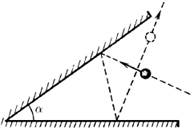
На какой угол изменится направление движения шара после двух упругих столкновений со стенками, угол между которыми равен α? Как полетит шар, если угол между стенками равен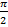 
? Движение происходит в плоскости, перпендикулярной стенкам.
Задача 7
Стрелок пытается попасть в диск радиуса R, который движется от одной стенки к другой с постоянной по модулю скоростью достаточно быстро, чтобы за ним нельзя было уследить. Нарисуйте график зависимости вероятности попадания пули в диск от расстояния между точкой прицеливания и левой стенкой. Выстрелы производятся на высоте R от пола, перпендикулярно направлению движения диска. Разберите случаи с различными расстояниями между стенками.
Движение с переменной скоростью.
Задача 1
Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющего одновременно двум условиям: средняя скорость в промежутке от 2 до 6 с равна 5 м/с, максимальная скорость в том же промежутке равна 15 м/с.
Задача 2
Частица, покинув источник, пролетает с постоянной скоростью расстояние L, а затем тормозится с ускорением a. При какой начальной скорости время движения от ее вылета до остановки будет наименьшим?
Задача 3
В коническом сосуде уровень воды поднимается с постоянной скоростью v0. Как зависит от времени скорость поступления воды в сосуд через трубку сечения s? В нулевой момент времени сосуд пуст.
Задача 4
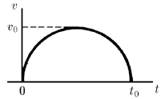
График зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела равна v0, время движения t0. Определите путь, пройденный телом.
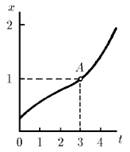
Задача 5
Графики зависимости координаты от времени, построенные в различном масштабе времени для двух частиц, оказались одинаковыми. Одно деление оси времени t для графика первой частицы отвечает 4 с, а для графика второй – 1 с. Найдите отношение скоростей и отношение ускорений частиц для точки А графика.
Задача 6
Тело начинает движение из точки А и движется сначала равноускоренно в течение времени t0, а затем равнозамедленно, с тем же по модулю ускорением. Через какое время от начала движения тело вернется в точку А?
Задача 7
Из одной и той же точки вертикально вверх с интервалом времени ∆t брошены два шарика со скоростью v. Через какое время после вылета второго шарика они столкнутся?