Арифметические действия над обыкновенными дробями

ПРАКТИЧЕСКАЯ РАБОТА № 1

«Развитие понятия о числе»

Цели урока:

1) Обобщить теоретические знания по теме «Развитие понятия о числе».

2) Рассмотреть алгоритмы решений заданий теме « Десятичные и обыкновенные дроби, приближенные вычисления, действия над комплексными числами», решить задачи.

3) Формировать тактичность; терпимость; умение доказать свою точку зрения при работе в коллективе.

Теоретический материал

Обыкновенные дроби.

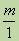Обыкновенная дробь - это число вида , где m и n - натуральные числа. Число m называется числителем дроби, n - знаменателем. Если n = 1, то дробь имеет вид , но чаще пишут просто m, т. е. любое натуральное число можно представить в виде обыкновенной дроби со знаменателем 1.

Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему. Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если m кратно n).

Принято сумму натурального числа и правильной дроби записывать без знака сложения, т. е. вместо 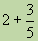пишут 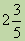. Число, записанное в таком виде, называется смешанным числом. Оно состоит из целой и дробной части.

Равенство дробей. Сокращение дробей.

Две дроб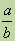и и 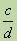считаются равными, если ad = bc. Из определения равенства следует, что 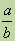= 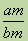, т. к. 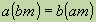. Основное свойство дроби: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной. Пользуясь основным свойством дроби, иногда можно заменить данную дробь другой, числитель и знаменатель которой меньше данных. Такая замена называется сокращением дроби. Если числитель и знаменатель - взаимно простые числа, то сокращение не возможно и такая дробь называется несократимой.

Арифметические действия над обыкновенными дробями.

Пусть даны две дроб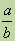и и 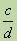, 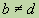. Можно заменить эти дроби другими, равными им, таким, что у полученных дробей будут одинаковые знаменатели. Такое преобразование называется приведением дробей к общему знаменателю. Обычно стараются привести дроби к наименьшему общему знаменателю, который равен Н.О.К.( ).

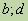1. Сложение обыкновенных дробей выполняется так:

а)если знаменатели одинаковые, то числители складывают и оставляют тот же знаменатель: ;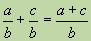

б) если знаменатели дробей различны, то дроби сначала приводят к наименьшему общему знаменателю, а затем применяют правило а).

2. Вычитание обыкновенных дробей выполняется следующим образом:

а)если знаменатели одинаковые, то

;

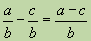б) если знаменатели дробей различны, то дроби сначала приводят к наименьшему общему знаменателю, а затем применяют правило а).

3. Умножениеобыкновенных дробей выполняется следующим образом:

.

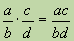4. Деление обыкновенных дробей выполняется следующим образом:

.
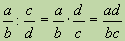