Закон Богуславского Ленгмюра

В вакууме Iн (ток насыщения) зависит от температуры катода. При увеличении температуры Iн растет, это объясняется увеличением эмиссии электронов, т.е. количеством вырываемых с поверхности катода электронов в единицу времени равно количеству е, достигших анода за то же самое время. С не зависит от температуры катода, а зависит от материала катода и чистоты его поверхности.

2) Магнитный момент атома По Бору атом- положительно заряженное ядро ( состоящее из протонов и нейтронов). I=eυ Круговой ток создает магнитный момент (который определен по правилу правого винта).

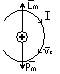Pm=IS=eυπr² Lm=mvr-орбитальный механический момент => Pm/Lm=-eυπr²/ mvr=- eυ2πrr/2mvr=-e/2m (‘-‘ означает противоположно направленные Pm и Lm) . Отличие магнитного момента, связанного с орбитальным движением электрона, к механическому моменту -величина постоянная и не зависит ни от радиуса отбиты ни от скорости его движения – это гиромагнитное отложение. Собственный механический момент е называется спином. Суммарный магнитный момент атома определяется орбитальным магнитным моментом, спиновым магнитным моментом и магнитным моментом ядра. Рат=Рm+Рs+Ря, но т.к. m_я>>m_е и Р_я>>Р_е, то в основном Рат=Рm+Р. Включим внешнее магнитное поле. На заряд действует сила Лоренца Fл=evB. Т.к. е движутся вокруг ядра, то между е и ядром возникает сила притяжения , которая обуславливает его центростремительное ускорение. F=ma(*)=e²/4πε₀r², ε_ί=-dФ/dt=-SdB/dt=-πR²dB/dt=-E2πR E=rdB/2dt. Т.к. F=eE=evdB/2dt, то (*)Fdt=d(mv)=mdv mdv=erdB/2. Т.к. v=ωR, то rdω=erdB/2m => dω=ed/2m; ∆ω=-e∆B/2m-частота нарморовой процессии.

1) Уединенный проводник – проводник, который удален от других проводников, тел и зарядов. Его потенциал:φ=q/4πε₀r. Из опыта известно, что различные проводники, будучи одинаково заряженными, имеют различные потенциалы, т.е. q=Cφ. Величину C=q/φ называют электроемкостью. Ёмкость определяется зарядом, сообщенному проводнику и изменяет его потенциал на единицу. Ёмкость проводника зависит от его размеров и формы и не зависит от материала. Если к заряженному проводнику приблизить другой проводник, внутри них возникают индуцированные заряды, причём ближайшими к проводнику заряду q будут заряды противоположного знака. Эти заряды ослабляют поле, создаваемое зарядом q, т.е. снижают потенциал проводника, что приводит к повышению его электроемкости. Потенциал заряженного шара радиуса R, находящегося в однородной среде, с диэлектрической проницаемостью ε, равен φ=q/4πεε₀R => q=4πεε₀Rφ

[C]=

2) Взаимная индукция. возьмем два контура 1 и 2. Первый контур создает через контур два магнитный поток Ф₂=L₂₁I₁. При изменении тока I1 в контуре 2 индуцируется ЭДС ε₁₂=- L₂₁dI1/dt Аналогично Ф₁=L₁₂I₂; ε₂₁=- L₁₂dI2/dt. Контуры 1 и 2 называют связанными. Коэффициенты проницаемости L₁₂ и L₂₁ называют взаимной индуктивностью контуров. Их величины зависят от формы и размеров L₁₂=L₂₁. Взаимное расположение контуров, а также от магнитной проницаемости окруж. контуры средн. через коэффициент взаимной индукции контуров выражается взаимная энергия W12: W12=L₁₂I₁I₂.

4)Дано: ω=δ²/ρ => δ=(ωρ)^1/2=(Qρ/Vt)^1/2=0,101 В/м

V=6см³

t=1 мин

Q=216 Дж

ρ=1,7*10^-8 Ом*м

Е-?

5)Дано: eU=mv²/2 v=(2eU/m)^½ B=μ₀I/2πr

U= 0,5 кВ На действует сила Лоренца F=evB*μ₀eI(eU)^½/πr(2m)^½

r=1 см =4,24*10^-16 H

I=10 A

F-?

3) 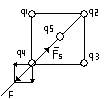Рассмотрим силу отталкивания положительных q=0,3 кН зарядов: F=F1+F2+F3 F1=q1q4/4πε₀α², F2==q2q4/4πε₀(α(2)^1/2)²,

F=F4 F3=q3q4/4πε₀α² Т.к q1=q2=q3=q4=q, то

q5-? F= q²(2)^1/2/4πε₀α²+q²/4πε₀α²2=q²(2(2)^1/2+1)/8πε₀α²

Т.к. силы должны быть уравновешены, то F=F5, гдеF5- сила притяжения зарядов q4 и q5. F5=q4q5/4πε₀(α(2)^1/2/2)²=4q4q5/4πε₀2α²=q4q5/2πε₀α²

т.е. q²(2(2)^1/2+1)/ 8πε₀α²=qq5/2πε₀α² => q5= q(2(2)^1/2+1)/4=2,8*10^-10Кл

1) Напряженность – сила, с которой поле действует на малый положительный заряд, внесенный в это поле. Это силовая характеристика поля: Е=F/q. Потенциал- энергетическая характеристика, которая численно равна работе , которую совершают силы поля над положительным зарядом при удалении его из данной точки в бесконечность. A∞=qφ => φ=A∞/q. φ=q/4πε₀α, A=q∆φ, => φ численно равен W/q. Связь между потенциалом и напряженностью такая же, как и связь между силой и работой: dA=Fdℓ=Eq₀dℓ. dA=φq₀-q₀ (φ+dφ)=-q₀dφ. E=-dφ/dℓ=-q∞dφ. Градиентом скалярной величины называется вектор, направленный в сторону возрастания этой величины и численно равный скорости изменения этой величины. grad φ противоположен по направлению вектору напряженности. Поверхность одинакового потенциала называется эквипотенциальной поверхностью. При перемещении по эквипотенциальной поверхности потенциал не меняется (dq=0) Следовательно касательная к поверхности составляющая вектора E=0 => вектор Е в каждой точке направлен по нормали к эквипотенциальной поверхности.

2) Теория Био-Савара-Лапласа. B~I. Предположим, что магнитная индукция – векторная величина и магнитная индукция подчиняется принципу суперпозиции магнитный полей: B=∑B_i. Idℓ - элемент тока, расстояние от которой до точки А равно v, α-угол между элементом тока и направлениями на точку. dB=μIdℓsinα/4πr²- закон Био-Савара-Лапласа.

5) Дано:

С=0,2мкФ T=2π/(1/4C-(R/2L)²)^1/2. Предположим, что R достаточно мало,

U=9,07*10^-3Гн тогда T=2π/(LC)^1/2=0,2*10^-3C. Разность потенциалов меняется по

t=10^-3с закону U=U₀exp(-2t/T), откуда Q=Tln(U1/U2)/t=0,2*10^-3ln3/10³=

U1/U2=3 =0,22. Q=βT=RT/2L, откуда R=2QL/t=11,1 Ом. Величина

Q-? (R/2L)²≈10³ намного меньше 1/LC≈10³ => можно было

применить формулу T=2π/(LC)^1/2

4)Дано: 1)j=I/S=ε/RS=37500 A/м²

ε=6В 2)j=Ne/St => N=jSt/e=εSt/RSe=εt/Re=7,63*10¹⁷

R=80 Ом

S= 2 мм²

t=1 c

j,N-?

3)Дано Напряжение поля E=б/2εoε, E=F/τl, б/2εoε=F/τl

б=20 нКл/м² Fl=4,5*10^-7 H

τ=0,4 нКл/м

l=1 м

F_l-?

5)С=2,2 Ф æ=βt=R2π(LC)^1/2/2L=πR(LC)^1/2

l=0,1 м L=μoμn²lS=μoμlS_кπ/4Sпр²

Sпр=1мм² Т.к. N=l/d, а n=N/l, то n=1/d, то n²=1/d²=π/4Sпр

ρ=1,7*10^-8 Ом*м R=ρlпр/Sпр, lпр=Nπυ=πυ/d=l(π)^1/2π2(Sк)^1/2/2(Sпр)^1/2(π)^1/2=

S=2*10^{-4 м2} =πl(Sк)^1/2/(Sпр)^1/2, R=(Sк)^1/2ρlπ/(Sпр)^1/2 Sпр

х-? R= π(Sк)^1/2 ρlπ(μoμlS_кπ/4Sпр)l/(Sпр)^1/2Sпр=(μ-?)

1) 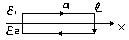Пусть в диэлектрике создано поле, напряженность которого в первом диэлектрике равна E1, во втором диэлектрике равна E2. Циркуляция вектора Е к контуру равно 0. 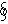Еdl=E_1xa-E_2xa+<E_l>dl, где <E_B>- среднее значение Е на перпендикулярных к ∫E_ldl=0 => (E_2x-E_1x)a=<E_B>2l при l→0 E_1x=E_2x . E_i=E_1m+E_1τ=> E_i=E_2m+E_2τ => E_1τ=E_2τ , где E_1τ –проекция E_i на орт I, направленный вдоль линии плоскости разделяющей диэлектрики с плоскостью, в которой лежит E1 и Е2. Т.к. D=εε₀E, то D_1τ / εε₁=D_2τ / εε₂ => D_1τ / D_2τ = εε₁/ εε₂ Возьмем на границе диэлектриков воображаемую поверхность высоты Н, основание S расположенную в первом диэлектрике, S1- во втором S1=S2=S и они постоянно малы, что в пределах каждого из них поле можно считать однородным. По теореме Гаусса Ф=∑q_i Если сторонних зарядов на границе между диэлектриками нет, то ∑q_i=0 => Ф=0. Поток через основание S1=D_1nS, где D_1n- проекция D на нормаль n1, S2=D_2nS, где D_2n- проекция D на нормаль n2. Поток через боковую поверхность равен <D_n>S_бок, тогда Ф=D_1nS+D_2nS+<D_n>S_бок=0, если n1→0, то →0, тогда Di=D_1mn появился из-за того, что n1, n2 направлены в разные стороны если спроецировать L и Di на одну нормаль, то D_1n=D_2n или ε₀ε₁E_1n=ε₀ε₂E_2n или E_1n / E_2n=ε₂/ε₁=> при переходе через границу раздела двух диэлектриков их средняя тангенциальная составляющая вектора Е к нормали остается постоянной, вектора D изменяется непрерывно, а нормальная составляющая вектора Е и тангенциальная составляющая вектора D претерпевают скачок.

2) Если проводник поместить в электрическое поле он начнет перемещаться под действием силы Ампера: F=ℓIBsina, где a- угол между I и dℓ, dF=dℓIBsina. Направление силы Ампера определяется правилом левой руки: 4 пальца вдоль направленных силовых линий магнитное поле в ладонь, то большой палец укажет направление силы Ампера dF=I[dℓB]. Работа по перемещению проводника с током: dF=dℓIBsina(dℓB) sin(dℓB)=1 тогда F=ℓIB dA=Fdx => A= ℓIB∫(0,x)dx=IBℓx=ISB=I∆Ф. где ∆Ф-изменение потока, возникшего вследствие перемещения проводника в магнитном поле. Работа совершается за счет ε источника.

3)Дано:

d1=10^-4м Возьмем систему из 3 конденсаторов соединенных

ε₁=7 последовательно.

d2=0,2*10^-4м 1/C=1/C1+1/C2+1/C3=2/C2+1/C1, C= ε₀εS/d

ε₂=2 C1= ε₀εS/d1 C2= ε₀εS/d2 1/C=2d2/ ε₀ε₂S+ d1/ ε₀ε₁S

S=0,02 м² =>C= ε₀ε₁ε₂S/2d2ε₁+d1ε₂=5,16*10^-9Ф

С-?

4)Дано: По II правилу Кирхгоффа: I: ε₁=I1R1+I_ε1r1

ε1=ε2=2 В II: - ε₁-ε₂=I2R2+ I_ε1r1+I_ε2r2.

По I правилу Кирхгоффа для узлов А и В:

r1=r1=0,5 Ом I1+I2- I_ε1=0 (A), I_ε2-I2-I1=0 (B) => I_ε2=I2

R1=50 Ом Тогда: - ε1=I1R1+I_ε2r2, - ε₁-ε₂=I2R2+ I_ε1r1+I_ε2r2, I1+I2=I_ε1.

R2=1б5 Ом Получили систему трех уравнений с тремя неизвестными.

I1,I2,I3-? - 2=50I1+0,5I_ε2, -4=2I2+ 0,5I_ε1, I1+I2=I_ε1

I2=0,63A, I1=11,15A, I_ε1=10,52A

5)Дано w_Iрез=1/LC, w_Uрез=(1/LC-2β²)^1/2

w_Uрез=99% w_Iрез Q=π/λ=π/β2π(LC)^1/2=1/β2(LC)^1/2

w-? w_Uрез/ w_Iрез=0,99 (1/LC-2β²)^1/2(LC)^1/2=0,99

(1-2β²LC)^1/2=0,99 2β²LC=0,0199

Q=(2/2β²LC) ^½=10

1)Потенциальность электрoстатистического поля. рассчитаем работу при перемещении заряда q1 в поле, создаваемом зарядом q при переходе из точки 1 в точку 2. A=-dlcosa. dlcosa=dr=> Fdr=q1qdr/4πε₀r² => A=∫dA=∫q1qdr/4πε₀r²=-q1q2/4πε₀r==-q1q2(1/r1-1/r2)/4πε₀ => работа при перемещении электрического заряда q1 в поле заряда q не зависит от выбора пути, а определяется лишь начальным и конечным положением перемещения по среде => электрическое статистическое поле потенциально. A132=A14. А132=-А241 А_пол=А3241=0 => работа перемещения зарядов в электрическом поле dA=!. Если q:1=F/q, то dA=Rdlcosa=(E^dl); A= 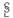(Edl)=0 циркуляция вектора направленного вдоль замкнутого контура равно о 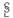(Edl)- циркуляция вектора напряженности.

2) Всякий реальный контур обладает активным сопротивлением. Энергия, запасённая в контуре, постепенно расходуется на нагревание и колебания затухают. По закону Ома R=φ1-φ2=ε12, где φ1 φ2 =-q/C ε12=-LdI/dt. IR=-q/C-dv/dt. Разделив уравнение на L и заменив I=q′,dI/dt=q′, получим q′′+Rq′/L+q/LC=0, т.к. ω₀²=1/LC, β=-LdI/dt, получим q′′+2βq′+ω₀²q=0 – дифференциальное уравнение затухающих колебаний. При условии, что β²<a, -ex²/4L²=1/4C. решение примет вид q=q_me^-βtcos(wt+a), где w=(w₀²-β²)^1/2 частота затухающих колебаний меньше собственной частоты w. U=U_me^-βtcos(wt+a) I=w₀q_me^-βtcos(wt+a+ψ), где sin ψ=w/(w²+β²)^1/2=w/w₀,cosψ=-β/ (w²+β²)^1/2=-β/w₀

Полная система дифференциальных уравнений Максвелла в дифференциальной форме wt*E=-∂β/∂t; divD=P; wtH=j+∂D/∂t;div B=0. Уравнение Максвелла – наиболее общее уравнение для электрических и магнитных полей в покоящихся срезах. Если заряды и токи непрерывно распределены в пространстве, то обе формы уравнений Максвелла эквиваленты. Сила тока определяется по фазе. Амплитуда убывает по закону е-^βt . Логарифмический декремент затухания λ=a(t)/a(t+T)=βT( где a(t) – амплитуда соответствующей величины) – обратен числу колебаний Ne, совершаемых за время, в течение которого амплитуда уменьшается в е раз.λ=1/Ne. λ=βТ=R2π/2Lw= Rπ/Lw. Частота w => и λ определяются параметрами контура L,C и R => логарифмический декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний.

3) Дано Пусть заряд “-“. F1+F2=0. F1=F2, т.к. равновесие. F1=kq1Q/x²,

q1=1,8*10^-7 Кл F2=kq2Q/(l-x)², kq1Q/x²= kq2Q/(l-x)² => 4x²=(0,6-x)²

q2=7,2*10^-7 Кл x=0,2 м

l=0,6 м

x-?

4)Дано: Iкз=ε/r, I1=E/(R1+r),I2=E/(R2+r) => I1(R1+r),I2(R2+r) =>

R1=50 Ом r=10Ом тогда ε=I1/(R+r)=0,2*(50+10)=12B

I₁=0,2 A

R2=110 Ом Iкз=12/10=1,2 A

I2=0,1 A

I_кз-?

5)Дано: H1=I1N/π =8380 А/м. по графику зависимости B от H B1

=11,4 см B1=1,8Тл. Тогда μ₁=B1/μ₀H1=171

N=200 B2=I2Nμ₀μ₁μ₂/(8μ₀+(π 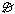-8)μ₁) т.к. μ₁=1 , то

I1=15A B2=I2Nμ₀μ₂/(8μ₀+(π 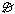-8)) =>

б=1 мин I2=22,1 A

I2-?

1) Электрический диполь – система двух одинаковых по величине, но противоположных по знаку зарядов, расположенных на малом расстоянии друг от друга. p=qℓ, гдеℓ- плечо диполя. Р направлен по оси диполя от отрицательного заряда к положительному. q+=q- => E+=E-, по принципу суперпозиции Eн=Е-+Е+. 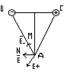Рассмотрим треугольник АВС и треугольник AMN, они подобны. Е-/E+=((r²+l²/4)^1/2/l)E+=E_-l/(r²+l²/4)^1/2=ql/4πε₀(r²+l²/4) (r²+l²/4)^1/2, т.к r>>l E_A=ql1/4πε₀r³=P/4πε₀r³- напряженность поля на перпендикуляре, восстановленном из сесредины диполя.

2)Явление самоиндукции IS=φ(направление винта). Если меняется сопротивление то меняется сила тока, меняется магнитный поток. A=В_инд:dФ/dt. то в самом контуре, по которому меняется ток, возникает ток индукции. Если значение тока увеличивается:dI/dt>0, то увеличивается магнитный поток (dФ/dt>0), тогда ток самоиндукции направлен так, чтобы препятствовать нарастанию тока (ε_si<0) Если dI/dt<0, то dФ уменьшается и убывающий поток обуславливает появление индуцированного тока(ε_si>0). Т.к. Ф~В, а В~I, то Ф~I, => Ф=LI, где L- коэффициент самоиндукции (индуктивность). Если ток в контуре равен –LR, то индуктивность численно равна магнитному потоку, пронизывающему этот контур [L]=Гн. Индуктивность зависит от размеров и формы контура, от магнитных свойств среды, в которой расположен контур.

H=nI, напряженность поля и оси соленоида (n – число витков на единицу длины). B=μμ₀H=μμ₀nI ψ=ФN (потокосцепление). N=nℓ. ψ=BSN=μμ₀nISnℓ=μμ₀n²ISℓ. L=μμ₀nV => индуктивность зависит от геометрических размеров и свойств среды. ε_si=-dФ/dt, Ф=LI => ε_si=-LdI/dt. Ток при размыкании I_n=I₀e^-Rt/L, ток при замыкании Is=I₀(1-e^-Rt/L). Коэффициент τ=L/R называется временем релаксации, это время, в течение которого сила увеличивается в е раз.

3)Дано ΔW=A dA=qdφ, где dφ – изменение потенциала

R=1 см E=τ/2πε₀r dφ=-Edr A=-q∫(R,R+r)Edr ->

τ=10^-5 Кл.м A=-q∫(R,R+r)τdr/2πε₀r=-qτ/2πε₀∫(R,R+r)dr/r=

r=4 см =-qτ/2πε₀ln((R+r)/R)=-9,27*10^-14 Дж= ΔW

q=3,2*10^-19 Кл

ΔW-?

4)Дано dA=I²Rdr I=Rr, где R=(I2-I1)/t Тогда A=∫dA=∫I²Rdr=

R=32 Ом =∫(0,t)(I2-I1)²rRdr/t²=)(I2-I1)²Rt³/3t²=(I2-I1)²tR/3=1280 Дж

t=5 с

I1=2A

I2=10A

A-?

5)Дано η=N/ N₀ P=εI=ε²/r – полная мощность

N₀,ε,r η=(N₀-ε²/r)/N₀=1- ε²/rN₀

η-?

1)Электрический заряд элементарная частица – количественная мера ее электромагнитного взаимодействия с другими частицами. Всякий заряд образуется совокупностью элементарных зарядов, он является целым кратным е: q=±Ne. Величина заряда измеряется в различных инерциальных системах отсчета оказывается одинаковой => не является релятивистки инвариантным, т.е. величина заряда не зависит от того движется он или покоится. Электрические заряды могут исчезать и возникать вновь. Всегда возникают и исчезают 2 элементарных заряда противоположных знаков. Нейтрон и позитрон при встрече превращаются в нейтральные гамма-фотоны. При этом исчезают заряды +е и –е. В ходе процесса, называемого рождением пары, гамма-фотоны, покидают поле атомного ядра, превращаются в частицы – электрон и позитрон. Т.е. суммарный заряд электрически изолированоой системы не меняется – это закон сохранения электрического заряда.

2)Энергия, запасённая в контуре, постепенно расходуется на нагревание., вследствие чего колебания затухают. Закон Ома: IR=-q/C-LdI/dt – разделив на L и заменив I через q′, а dI/dt через q′′, получим q′′+R q′/L+q/LC, ω₀²=1/LC, β=R/2L, => q′′+2βq′+ω₀²q=0 – дифференциальное уравнение затухающих колебаний. При условии β²<<ω₀², т.е. R²/4L²<1/LC решение уравнения имеет вид q=q_me^-βtcos(wt+a), где w=(w₀²-β²)^1/2; w=(1/LC- R²/4L²)^1/2 => частота затухающих колебаний w меньше собственной частоты колебаний w₀. Логарифмический декремент затухания x=lna(t)/a(t+τ)=βτ, где a(t)- амплитуда соответствующей величины. Декремент затухания обратен числу колебаний Ne, совершаемых за время, в течение t амплитуда уменьшается в e раз. x=1/Ne. Заменив T через 2π/ω => λ=R2π/ω2L= Rπ/ωL => λ определяется параметрами контура β=R/2L называется коэффициентом затухания. T=1/ω=1/(1/LC- R²/4L²)^1/2

4)Дано По II закону Кирхгоффа: IR+I₁r₁=ε₁ IR+I₂r₂=ε₂

ε₁=2 В По I правилу Кирхгоффа: I=I1+I2 =>

ε₂=3 В I=(r₂ε₁+r₁ε₂)/(Rr₁+r1r₂+Rr₂) Заменим батарею I=ε/(R+r), где

r₁=1 Ом 1/r=1/r₁+1/r₂ =>r=r₁r₂/(r₁+r₂) ε=(R+r₁r₂/(r₁+r₂))(r₂ε₁+r₁ε₂)/(Rr₁+r1r₂+Rr₂)=

r₂=1,5 Ом =2,4 B r=0,6 Ом

R=20 Ом

r-?

5)Дано I=e/T где Т период вращения е T=2πR/v S=πR²=>

е=1,6*10^-19 Кл P_m=IS=evπR²/2 πR=evR/2 L=mvR =>

m=9,1*10^{-31 кг} P_m/L=evR/2nvR=e/2m=87,9*10⁹Кл.м

P_m/L-?

1) Диэлектрики – вещества, в которых нет свободных электрических зарядов. Диэлектрик состоит из атомов и молекул и в целом электрически нейтрален. Диэлектрики бывают неполярными (центры тяжести “+” и “-“ зарядов находятся в одном месте),напримерCH₄, и полярными (центры тяжести не совпадают), например H₂О. Рассмотрим электрическое поле между обкладками конденсатора, если в него внести диэлектрик. Е₀ – поле, создаваемое свободными зарядами на металлических пластинах (внешнее поле). Во внешнем поле диэлектрик поляризуется. Е′- электрическое поле, создаваемое связанными зарядами. Е=Е₀+Е′ векторно или Е=Е₀-Е′=Е₀-ύ/ε₀=Е₀-p_m/ε₀= Е₀-λ_nε₀E/ε₀= Е₀-λ_nE. E+λ_nE =Е₀=E+æE; 1+æ=ε, E₀=εE => ε= E₀/E- величина, указывающая во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике, называются диэлектрической проницаемостью. Линии напряженности электрического поля на границе диэлектриков претерпевает разрыв E1=E₀/ε₁ E2= E₀/ε₂ D=εε₀E – вектор электрического смещения (Кл/м²). Теорема Гаусса: Ф=∑qi – поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности сторонних зарядов.

2) Термоэлектронная эмиссия- вырывание электронов из металла при его нагревании. В металле имеются валентные е, которые выступают в роли свободных е. Во втором случае притяжение со стороны ионов Wпот<0 (т.к. притяжение), Wкин=mv²/2>0. Если [Wпот]>[Wкин], то е не может покинуть металл. Если [Wкин]>[Wпот], то е способен вылететь, при этом в металле остается дырка, е может вернуться туда, но наиболее быстрые не возвращаются, т.е вблизи поверхности металла образуется двойной электрический слой. Wпот=0 при Т≠0 К. Даже при Т=0 К е в атоме металла не находится на дне потенциальной дамы в силу волновых свойств тока. Энергия, которой обладает е при Т=0 К – Энергия Ферми Wк. С увеличением температуры энергия Ферми практически не меняется. Минимальная энергия, которую нужно сообщить е, чтобы перевести из металла в вакуум, называется работой выхода. Т.к. Wпот<0, то выход означает повышение Wпот до 0 [Авых=eU] . Термоэлектронная эмиссия – вырывание е из металла при нагревании. Если энергия теплового движения е равна Wтепл=3kT/2 , то энергия, необходимая для вырывания е соизмерима с Wтепл. W= Wпот-Wк => Wтепл при Т≈15000 К. Вырывание происходит при 1000-3000 К. Скорость при этом изменяется от min до max. Эмиссию легко наблюдать в вакуумном диоде. Катод нагревают до 1000-9000 К. Вблизи катода образуются электронные облака, и если прижито анодное направление U_A, то возникает направленное движение е и потечет электрический ток. Сам вакуум не проводит электрический ток. Для е при столкновении ионов в металле. В вакууме же е не испытывают столкновений, поэтому зависимость силы анодного тока от U не линейная I_A=CU^3/2 Для е при столкновении с ионами в металле и вакууме е не испытывает столкновений и зависимость силы тока от напряжения нелинейная I_A=CU_A^3/2 – закон Богуславского-Ленгмюра. I_нас зависит от температуры катода, при повышении температуры этот ток растёт, это объясняется увеличением эмиссии электронов. При I_нас количество вырванных с поверхности катода электронов в единицу времени равно количеству е, достигших анода за о же самое время, е не зависит от температуры катода, а зависит от материала катода и частоты его поверхности.

3)Дано Т.к. шар в равновесии, то mρ+F_эл+F_А=0 или mρ=F_эл+F_А,где

R=0,5 Ом mρ=ρVg=ρ_ш4πR³g/3, F=Eq

ρ_m=98*10³кг/м³ F_A=ρ_mVg= ρ_м4πR³g/3=Eq+ρ_м4πR³g/3 => Eq=4πR³g(ρ_ш-ρ_m)/3

E=10⁴В/м => q=4πR³g(ρ_ш-ρ_m)/3E=4 мкКл

ρ_ш=8,6*10³кг/м³

q-?

4)Дано dQ=I²Rdt, I=vt, v=(I_max-I₀)/t Q=∫dQ=∫(0,1)v²Rt²dt=v²Rt³/3=

I₀=0A =I_max²Rt³/t²=> Imax=(3Q/Rt)^1/2=1A/c

t=10c

Q=1 кДж

R=3 Ом

v-?

1)Под Действием внешнего электрического поля заряды в неполярной молекуле смещаются друг относительно друга. Положительные по направлению поля, отрицательные против поля. В результате частица приобретает дипольный момент, причём P=βε₀E, где Р – дипольный момент, β – поляризованность молекулы. Процесс поляризации неполярной молекулы протекает ток, как если бы “+” и “-“ заряды молекулы были связаны друг с другом упругими силами. Поэтому неполярная молекула ведет себя как упругий диполь. Действие внешнего поля на полярные молекулы сводится в основном к стремлению повернуть тк, чтобы её дипольный момент установился по направлению поля. Поляризованная молекула ведёт себя как жёсткий диполь. В качестве величины, характеризующей степень поляризации диэлектрика берут дипольный момент единицы объёма. P=∑P – поляризованность диэлектрика P=λε₀E, где λ – диэлектрическая восприимчивость диэлектрика (безразмерная величина).

2)Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток. Бесконечно длинным считается соленоид, длина которого во много раз больше, чем диаметр его витков. Поле такого соленоида сосредоточено целиком внутри него. Выберем замкнутый контур ABCDA. 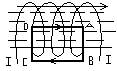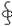(BCDA)B_ldL=μ₀NI, на участках AB и CD контур перпендикулярен линиям магнитной индукции, поэтому B_l=0; на участке вне соленоида В=0. На участке DA циркуляция В равна B_l => 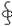(DA)B_ldL=B_l=μ₀NI => В=μ₀NI/l=μ₀NI, где nm- число витков на единицу длины B=μ₀NI. Поле внутри соленоида одноролно (краевыми эффектами в областях, прилегающихсторонам соленоида пренебрегают).

3)Дано δ′=ε₀(ε-1)Е, Е=q/4πε₀x² δ₁′=ε₀(ε-1)Е ==ε₀(ε-1)q/4πε₀h²=

h=3 см =q(ε-1)/4πh²=1,5 мКл/м²

q=17*10^-9Кл δ₂′=q(ε-1)/4πr²=5,4*10^-7 Кл/м²

r=5 cм

ε=2 (спросить)

δ₁′, δ₂′-?

4)

Rv=300 Ом По II правилу Кирхгоффа I: ε₁=I1(R1+R4)-IvRv

ε1=ε2=2,2B ε₂=I2(R2+R3)-IvRv

R1=100Ом По I правилу Кирхгоффа I1+I2=Iv

R2=200Ом I1=(ε₁+IvRv)/(R1+R4) I2=(ε₂+IvRv)/(R2+R3)

R3=300Ом (ε₁+IvRv)/(R1+R4)+(ε₂+IvRv)/(R2+R3)=I_r => ε₁(R2+R3)+

R4=400Ом +IvRv(R2+R3)+ε₂(R1+R4)+IvRv(R1+R4)=I_r(R1+R4)(R2+R3)

Uv-? Ir=(-ε₁(R2+R3)-ε₂(R1+R4))/(Rv(R2+R3)+Rv(R1+R4)-(R1+R4)(R2+R3))

5)Дано ψ=LI; ψ=NФ=NBS => LI=NBS => B=LI/NS=114 Тл

S=20 см² В=μμ₀H => μ=B/μ₀H. По графику зависимости В от Н магнитного поля

N=500 Н=0,8*10³ А/м μ=114/4π*10^-7*0,8*10³=1400

L=0,29 Гн

I=5А

μ-?

=0,032A Uv=IvRv=9,6B

1)Теорема Гаусса. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑q_i/ε₀. Напряженность поля бесконечно заряженной поверхности: под поверхностной плотностью заряда δ понимают заряд приходящийся на единицу поверхности δ=q/S (Кл/м²). Размеры поверхности >> расстояния, на которую рассчитывается напряженность – бесконечная поверхность. Поток через вспомогательную цилиндрическую поверхность, образующие которой параллельны линиям напряженности. N=Nбок+2Nосн=ESбок*сosπ/2+2ESосн*cos0=2ESосн. Из теоремы Гаусса N=∑q_i/ε₀ => ∑q_i/ε₀=2Eосн => Е=∑q_i/∑Е_оснε₀=δ/2ε₀ Для двух поверхностей – (+) – (-)

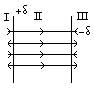Из принципа суперпозиции EI=EIII=0. EII=E₊+[E-]=2δ/2ε₀= δ/ε₀=> Напряженность поля бесконечной плоскости конденсатора не зависит от расстояния между пластинами, электрическое поле однородно и сосредоточено между пластинами.

2)Если магнитный момент P_m атомов равен 0, то вещество является парамагнетиком. Магнитное поле стремится установить магнитные моменты атомов вдоль В, тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля тем больше, чем > В, и тем меньше, чем выше температура. λкм=С/T – закон Кюри, где С-постоянная Кюри, зависящая от рода вещества, λкм – восприимчивость парамагнитного вещества. С=μ₀N_AP_m2/3k, тогда λкм μ₀N_AP_m2/3kT. Здесь предполагается, что P_mB<<kT. В очень сильных полях и при низких температурах наблюдается отступление от пропорциональности между намагниченность парамагнетика I и напряженностью поля Н, в частности, может наступить состояние магнитного насыщения, при котором все P_m выстраиваются поп полю и дальнейшее увеличение Н не приводит к увеличению I.

3)Дано dφ=rdl/4πε₀r, где r – расстояние от точки , в которой определяется

q=10^-2Кл потенциал до элемента стержня dl=rda/cosa => dφ=rda/4πε₀cosa

φ-? φ=∫(a1,a2)rda/4πε₀cosa Т.к. точка симметрична относительно концов стержня, то ф1=ф2 и φ=2r/4πε₀∫(0,a1)a/cosa=2r/4πε₀lntg(a/2+π/4)│(0, π/4)= 2r/4πε₀lntg(π/3)=988B

4)Дано

ε₁=11 В По I закону Кирхгоффа: I2=I1+I3

ε₂=14 В По II закону Кирхгоффа: ε₁-ε₂=I1R1+I2R2 ε₃-ε₂=I3R3+I2R2

ε₂=16 В Получим схему из трех уравнений с тремя неизвестными.

R₁=50 Ом ε₁-ε₃=I1R1-I3R3=I1R1-I3R1-I3R3=I1R1-I3(R1+R3) =>

R₂=10 Ом I2=(ε₁-ε₃+I3(R1+R3))/R1, из 3 уравнения I2= (ε₃-ε₂-I3R3)/R2 =>

R₁=2 Ом (ε₁-ε₃+I3(R1+R3))/R1= (ε₃-ε₂-I3R3)/R2 =>

I1,I2,I3-? (ε₁-ε₃)R2+I3R2(R1+R2)=(ε₃-ε₂)R1-I3R1R3 =>

I3=(R1(ε₃-ε₁)- (ε₁-ε₃)R2)/(R2(R1+R2)+R1R2)=0,242 A

I2= (ε₃-ε₂-I3R3)/R2 =0,152 A I1=I2-I3=-0,09A

5)Дано 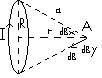Выберем элемент тока в точке 4 он создает поле dB=

R=0,2 м =μμ₀I[dl,r]/4πr². вс силу симметрии суммарный вектор В напрвлен вдоль

r=0,3 м оси х => для нахождения модуля вектора индукции сложим проекции

В=0,20 мкТл всех векторов dB на ось Ox: dBx=dBcosa=μμ₀Idlcosa/4π cosa=R/a,

I-? a=(r²+R²)^1/2 ∫dB=∫ μμ₀IdlR/4π ((r²+R²)^1/2 )^3/2= μμ₀IR/4π ((r²+R²)^1/2 )^3/2∫(0,2πR)dl=

=μμ₀IR²/2((r²+R²)^1/2 )^3/2 I=2B((r²+R²)^1/2 )^3/2/μμ₀R² μ-?

1)Теорема Гаусса. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑q_i/ε₀. Напряженность поля бесконечно заряженной поверхности: под поверхностной плотностью заряда δ понимают заряд приходящийся на единицу поверхности δ=q/S (Кл/м²). Размеры поверхности >> расстояния, на которую рассчитывается напряженность – бесконечная поверхность. Поток через вспомогательную цилиндрическую поверхность, образующие которой параллельны линиям напряженности. N=Nбок+2Nосн=ESбок*сosπ/2+2ESосн*cos0=2ESосн. Из теоремы Гаусса N=∑q_i/ε₀ => ∑q_i/ε₀=2Eосн => Е=∑q_i/∑Е_оснε₀=δ/2ε₀ Для двух поверхностей – (+) – (-)

Из принципа суперпозиции EI=EIII=0. EII=E₊+[E-]=2δ/2ε₀= δ/ε₀=> Напряженность поля бесконечной плоскости конденсатора не зависит от расстояния между пластинами, электрическое поле однородно и сосредоточено между пластинами.

2)Магнитная взаимоиндукция параллельных токов. F 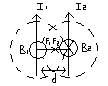_A=ℓIBsina, по закону Ампера на 1 проводник действует сила F1=I1B1ℓ1 (sina=1), направление которой определяется по правилу левой руки. На второй проводник действует сила F2=I2B2ℓ2 => два параллельных проводника по которым текут токи одного напряжения , притягиваются. Магнитная индукция прямого тока B=μ₀I/2πd, то (ℓ1=ℓ2). F1=I₁μ₀I₂ℓ/2πd F2=I₁μ₀I₂ℓ/2πd => F1=F2 F=I₁μ₀I₂ℓ/2πd - сила магнитного взаимодействия токов. F=I₁μ₀I₂/2πd- сила магнитного взаимодействия, приходящаяся на единицу длины.

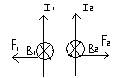аналогично, сила взаимодействия определяется также соотношением F2=I₁μ₀I₂ℓ/2πd. Сила тока – величина заряда, прошедшего через поперечное сечение проводника в единицу времени I=dq/dt. Единицей измерения силы тока является 1 ампер (А), устанавливаемый по магнитному взаимодействию тока. За единицу силы тока принимают силу тока, при которой отрезки 2-х параллельных проводников длиной 1 метр каждый взаимодействует с силой 2*10^-7 Н

3) Дано на электрон действует постоянная сила F=eE, над действием

U=300В которой он получит ускорениеa=eE/m. Пролетая длину ℓ контура

d=2 см за время t=1/v, е отклонится на расстояние y=at²/2=eEt²/2mv² ,

ℓ=10 см чтобы электрон не вылетел из контура, должно выполняться условие

v₀-? y>=d/2 => предельная скорость v₀=ℓ(Ee/md)^1/2=3,64*10⁷ м/c

4)Дано: dQ=I²Rdt, где I=kt, k=(I0-I)/τ=1/2=0,5

R=12 Ом Q=∫dQ=∫(0,τ)k²Rt²dt= k²Rt³/3=1 кДж

I0-5A

I=0

τ=10 c

Q-?

5)Дано При t→∞ Imax I=ε(1-e^-(r+R)∞/L)/(R+r)=Rε/(R+r)

r=1 Ом I=0,99Imax= ε(1-e^-(r+R)t/L)/(R+r)

L=0,5 Гн 0,99 ε/(R+r)= ε(1-e^-(r+R)t/L)/(R+r) e^-(r+R)t/L=0,01

R=8 Ом t(R+r)/L=ln100

τ=99% t=ln100*L/(R+r)=0,23 c

t-?

1) dA=-dW А=qq₁/ 4πε₀r₁-qq₂/ 4πε₀r₂ =-∆W W1=qq₁/ 4πε₀r₁ W2= qq₂/ 4πε₀r₂ Величина φ=W/q называется потенциалом поля и численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. φ=q/4πε₀r => A=(q1(φ2-φ1). Потенциал является энергетической характеристикой поля, Е – силовая характеристика. φ=А∞/q₀, т.к. потенциал равен работе, которую совершили силы поля над единичным положительным зарядом при удалении его из данной точки в ∞. Связь между потенциалом и напряженностью такая же, как и связь между силой и работой dA=-Fdl=qEdl, dA=φq₀-qd(φ+dφ)=-q₀dφ => Edl=-q₀dφ , E=-dφ/dl=-gradφ – взаимосвязь между напряженностью и потенциалом. Градиентом скалярной величины называется вектор, направленный в сторону возрастания этой величины и численно равный скорости изменения этой величины. Градиент φ противоположен по направлению вектору напряженности. Поверхность одинакового потенциала называется эквипотенциальной поверхностью.

2) Уравнения Максвелла: I: 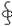(L)E_Bdl=- 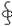∂B_ndS/∂t -> изменяющееся Вов ремени магнитное поле является причиной возникновения электрического поля магнитной природы (оно вихревое) II: 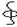(L)Hdl=∫(jпр+ jан)/dS=∫(jпр+∂D/∂t)dS изменяющееся во времени электрическое поле вызывает появление магнитного поля наряду с током проводимости. III: 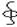DdS=∑qi – Теорема Гаусса для поля D поток вектора смещения электростатического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов. IV: 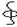BdS=0 – теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю.

3)Дано В силу симметрии в суммарную напряженность делают вклад

r=5 см только горизонтальные составляющие q=∫dq=τ2πr

τ=1мкКл/м dE=dq/4πε₀a²=dq/4πε₀(R²+r²) dEx=dEcosa, cosa=R/q

R=10см т.е. dEx=Rdq/(R²+r²)^3/2; E_A=∑dEx∫(0,q)Rdq/4πε₀(R²+r²)=

Е-? =2πτrR/4πε₀(R²+r²)=2,83 кВ/ м

4)Дано Источники можно подсоединить либо параллельно, либо последовательно

ε₁=1,5 В Пари последовательном подключении ε=nε₁=12*1,5=18 В, к=nr1=4,8 Ом

n=12 При параллельном соединении ε= ε₁=1,5 В, r= r1/n=0?0333 Ом

r1=0,4 Ом По закону Ома I=ε/R+r в первом случае при последовательном соеди-

R= 0,3 Ом нении I1=18/0,3+4,8=3,53 A во втором случае при параллельном соеди-

Imax-? нении I2=1,5/0,3+0,033=4,5 A => Imax=4,5 и он получается при параллельном соединении элементов.

1) Для равновесия зарядов на проводнике необходимо выполнение следующих условий: 1) Напряженность поля внутри проводника равна нулю Е=0, это означает, что потенциал внутри проводника должен быть постоянным (φ=const0. 2) Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормалям поверхности. Если проводящему телу сообщить заряд q, то он распределится так, чтобы соблюдались условия равновесия. Возьмем произвольную замкнутую поверхность, полностью заключенную в пределах тела. При равновесии зарядов поле в каждой точке внутри проводника отсутствует, поэтому поток вектора электрического сменщения через поверхность равна нулю. Согласно теореме Гаусса сумма зарядов внутри поверхности также равна нулю, при равновесии ни в каком месте внутри проводника нет избыточных зарядов – он распределяется по поверхности проводника с некоторой плотностью δ. Возьмём цилиндрическую поверхность, образованную нормалями к поверхности проводника и основаниями dS. Поток вектора электрического смещения через внутреннюю часть поверхности равен 0, т.к. внутри проводника D и Е=0. Вне проводника в непосредственной близости к нему напряженность направлена по нормалям к поверхности. Поэтому для выступа наружу боков поверхности цилиндра Dn=0, а для внешнего основания Dn=D => поток смещения через рассматриваемую поверхность равен DdS. Внутри цилиндра содержится сторонний заряд δdS/δ – плотность заряда в данном месте поверхности проводника. По теореме Гаусса получим: DdS=δdS, т.е. δ=D => E=δ/ε₀ε

Плотность зарядов при данном потенциале проводника определяется кривизной поверхности – она растет с ростом положительной кривизны (выпуклости). особенно велика бывает плотность зарядов на остриях. Рассмотрим поверхность такой формы. на больших расстояниях от проводника эквипотенциальные поверхности имеют форму сферы, По мере приближения к проводнику. Вблизи выступов эквипотенциальной поверхности располагаются => напряженность поля здесь больше => плотность зарядов на выступах

2) Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока приведёт к тому, что поле внутри проводника исчезнет и ток прекратится. Чтобы поддержать ток, надо от конца проводника с меньшим потенциалом непрерывно отводить приносимые сюда током заряды, а к концу с большим потоком непрерывно их подводить. Циркуляция вектора напряженности электростатического поля равна 0. Поэтому в замке цепи наряду с участками, на + положительные носители движутся в сторону убывания φ, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания φ, т.е. против сил электростатического поля. Перемещение носителей на этих участках возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними. Сторонние силы можно охарактеризовать работой , которую они совершают над перемещающимися в цепи зарядами. Величина, равная работе сторонних сил над единичным положительным зарядом, над электродвижущей силой. (ЭДС) ε=Аст.q. Fст =E′q, где E′ - напряженность сторонних сил. Аст=∫Fстdl=й∫E′вд – падение на q. Для замкнутой цепи ε= 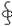E′вд – циркуляция вектора напряженности сторонних сил.

3)Дано A=W1-W2 Суммарный заряд остался первоначальным

С1=600 нФ q=CU. При последовательном подключении 1/C′=1/C1+1/C2

С2=1000нФ C′=C1C2/(C1+C2)

U=20кВ Фаза q= UC1C2/(C1+C2) и W1=q²/2C′= (UC1C2/(C1+C2))²/2C1C2/(C1+C2)=

А-? =C1C2U²/2(C1+C2)=0,075 Дж

При параллельном соединении С′′=С1+С2 и W2= q²/2C′′=(UC1C2/(C1+C2))²/2(C1+C2)=

=C1C2U²/2(C1+C2)=0,0175 Дж А=W1-W2=0,075-0,0175=0,057=57мДж

4) Дано

I₀=10A R_Ш= R_A/(n-1), где n=I₀/I n-1= R_A/ R_Ш n= R_A/ R_Ш+1

R_A=0,02 Ом I= I₀/n= I₀/(R_A+1)=2A n=5 R_Ш= ρℓпр/S =>

R_Ш=0,005 Ом ℓпр =SR_Ш/ ρ=0,0588=6см

S=0,2 мм²

ρ=1,7*10^-9 Ом*м

n=5

I,ℓпр-?

5)Дано Um=qm/C Im=ω₀qm= qm/(LC)^1/2

ε=8пФ Um=(L/C)^1/2Im=2 B

L=0,02 Гн

Imax=40 мА

Umax-?

1)Теорема Гаусса. Е поля для бесконечного цилиндра. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑q_i/ε₀. E=F/q, E=q/4πε₀r², - для точечного заряда. Для системы точечных зарядов Е=∑Еi, силовые линии показывают на направление сил. густота определяет модуль Е, N=E_nS – число линий. Ионизирующая поверхность перпендикулярна силовым линиям. или N=EScos(n^E). dN=E_ndS- элементарный поток. τ=q/ℓ- линейная плотность заряда. Построим вспомогательный цилиндр, высота которого равна H, а радиус r. Точка А находится на вспомогательной поверхности, а образующая параллельна оси заряженного цилиндра. N=Nбок+2Nосн, Nосн=0 => N=Nбок=ESбокcos(n^E)=0, cos0=0 => N=ESбок; Sбок=2πh => N=E2πrh т.к. N=∑q_i/ε₀,то [E=∑q_i/2πrhε₀=τ/2πrε₀] => напряженность поля безименного цилиндра нгеоднородно и является величиной, обратно зависящей от расстояния E=f(1/v). Eвнутр.=0

2)Ток смещения. Изменяющееся во времени магнитное поле вызывает появление эл. п

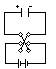Рассмотрим схему. В момент переключения ключа начинается перезарядка, лампа загорится. Если переключение делать с частотой 50 Гц. по 100 раз в секунду лампа будет вспыхивать и гаснуть. Если есть изменения эл. п., то оно замыкает цепь, дается возможность току вызывать горение лампы. Изменяющееся во времени поле между обкладками конденсатора называется током смещения. Единственным свойством, объединяющим его с током проводимости является вызывание им м. п. D=εε₀S. При зарядке конденсатора вектор D растет, т.е. ∂D/∂t>0 по направлению с D. При разрядке ∂D/∂t<0 и ∂D/∂t противоположен направлению D. Переменное эл. поле замыкает ток проводимости в проводящих проводниках вызывает включение лампы. I=Iпр+Iси. dℓ=∑Iпр (проводящий контур) ; Hdℓ=∑Iси( если есть -> вихревой магнитный изменяющийся ток) Iпр=dq/dt=dδdS/dt, Iпр/S=jпр=∫∂δ/∂t; D= εε₀S ; E=δ/ εε₀ => D=δб ja=∂Ф/∂t, (L)Hdℓ=∫(jпр+Ja)dS=∫(jпр+∂Ф/∂t)dS- IIуравнение Максвелла. III: 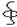DdS=∑qi. IV: 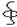BdS=0. B=μμ₀H, j=λE, 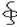Eqdℓ=0 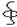E_Bdℓ≠0 И электрическое и магнитное поля вообще являются вихревыми, но электростатическое поле передвигает заряды потенциально. Hdℓ=∑jпр (I- постоянный). Hdℓ=∑Iполн=Iпр+Iси. В быстропеременном электрическом поле с диэлектрической средой преобладает Iси

3)Дано δ₁′=ε₀(ε-1)E , E=q/4π ε₀ε(R+x)² => δ₁′=ε₀(ε-1)q/4π ε₀ε(R+x)²=

R=0,05 м =q(ε-1)/4π ε(R+x)², соответственно δ₁′=q(ε-1)/4π εR²,

x=0,02 м δ₁′=3,3*10^-7Кл/м δ₂′=2,5*10^-7Кл/м

ε=5

q=10⁸ Кл

δ₁′,δ₂′-?

4)Дано dq=Idt Ток изменяется по II закону I=kt, где k=(I-I/2)/t=I/2t

I=189А I=2kt, dq=2ktdt, q=∫dq=∫(0,t)Idt=∫(0,t)2ktDt=2kt²/2=It/2

I=0 q=Ne Ne=It/2, N=It/2e=0,6*10¹⁹

t=0,03 с

N-?

5)Дано n=ω/2π, => ω=2πn, ε=dФ.dt, ε_max=I_maxρ4a/S

В=0,1 Тл Ф=NBSsinωt, ε=NBSωcosωt: ε_max=NBSω

N=100 NBSω=I_maxρ4a/S, NBa²2πn=I_maxρ4a/S

а=0,2 м n=2Imaxρ/NBaπS=0,01 об/c

S=10^{-6 м2}

ρ=0,017*10^-6 Ом*м

Imax=2 А

n-?

3)Дано ε_is=-LdI/dt=> L=μμ₀N²S/ℓ [ε_is]= μμ₀N²πd²dI/4ℓdt

ℓ=0,5 м [ε_is]= ε_is/N= μμ₀Nπd²dI/4ℓdt, Iк=[ε_is]/R, R=ρℓк/S, ℓк=πd

d=3 м Iк=[ε_is] ε_is/ ρπd=μμ₀NSкddI/4ℓρdt=1,66 мА

N=1500

∆I=0,2 А

β=17 нОм*м

k=3 мм²

Iк-?

4)Дано шунт подключен параллельно амперметру => I= I_A+I_ш , U_A=U_ш=>

R_A=0,16 Ом I_AR_A= I_ш R_ш , I=40A

R_ш=0,094 Ом

I_A=8A

I-?

1) Энергетическая система точечных зарядов, заряженного конденсатора, проводника электрического поля. Считается, что потенциальная энергия на бесконечности равна 0, а изменение потенциальной энергии равно работе сил электрического поля, кроме того считается, что q1 неподвижен, а q2 движется из ∞ в точку удаленную от q1 на r12. A2=q2(0-φ2)= [q2φ2], где φ1 – потенциал точки поля, куда перемещен 2 заряд φ2=q2/4π ε₀r12,A2=q1q2/4π ε₀r12. Работа по перемещению 1 заряда : A1=q1(0-φ1)= -q1φ1, φ1=q1/4π ε₀r12,A2=q1q2/4π ε₀r12.=> A1=A2; W12=A1=A2=(q1φ1+q2φ2)/2. Внесем заряд q3, приближая его из ∞ в точку на расстояние r13 и r23. Работа по перемещению 3 заряда: A=A1+A3=A2+A3= q1q2/4π ε₀r12+q3(q1q2/4π ε₀r13+ q1q2/4π ε₀r23)=4/4πε₀2(q1(q2/r12+q3/r13)+q2(q1/r12+q3/r13)+q3(q1/r13+q2/r23))1/2[q1φ1+q2φ2+q3φ3]=> φ1=q2/4π ε₀r12+q3/4π ε₀r13. Увеличивая количество полученных зарядов, можно подсчитать энергию системы , прибавляя новые величины => ∑qnφn/2, где φ2-потенциал той точки поля, в которой находится заряд qn, а поле создается всеми n зарядами. Энергия заряженного конденсатора сосредоточена в поле конденсатора. ∆A=∆qU; C=∆q/U,∆q=CU => ∆H=C∆UU, A=∆Wp=∫dA=∫(0,U)CUdU=CU²/2. Wp= CU²/2=q²/2C=qU/2 – потенциальная энергия заряженного конденсатора. ω=W/V=εε₀E²/2 – объемная плотность энергии , зависит от материала диэлектрика и напряженности электрического поля в диэлектрике. Wp= CU²/2=q²/2C=qφ/2 – потенциальная энергия заряженного проводника.

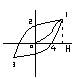2)Ферромагнетики. Вещества, способные обладать намагниченностью в отсутствие внешнего м. п. При внесении ферромагнетика в м. п. вектор намагниченности ведёт себя так: при Н=0, I=0, при увеличении Н растет и I, но при уменьшении Н кривая изменяет вид и при Н=0 есть остаточная намагниченность I₀≠0, при I=0 Нк≠0. Напряженность Нк при I=0 называется коэрцитивной силой. Петли гестеразиса: 0-1 – увеличение Н, 1-2 – уменьшение Нб 0-4- коэрцитивная сила, необходимая для снятия остаточного напряжения. Нк определяется по Max петле. Ферромагнетики делят на жесткие (если I₀ велико) и мягкие (I0 число) жесткие - основа для изготовления постоянных магнитов, мягкие – для трансформаторов. Т.к. ф-ия I=f(H) нелинейная, то ферромагнетик имеет μ, непостоянную для данного вещества. Ферромагнетик состоит из доменов – областей стоптанного намагничивания, который обладает определенным магнитным моментом при Т≠0 магнитные моменты в сумме дают 0. При внешнем вращении м. п. намагниченность увеличивается (0-1)- это область упругого смещения частиц доменов. Если выключит м. п. магнетик снова размагнитится. При дальнейшем увеличении внешнего м. п. намагниченность растет быстрее (1-2) – область неупругого смещения границы доменов и увеличиваются размеры доменов с малым углом за счет других доменов (2-3) – область вращения магнитных моментов доменов и установление их вдоль внешнего м. п. 3-4 – область парапроцессов при очень сильных полях. т.е. домены, которые имеют противоположный вектор, выстраиваются вдоль внешнего м. п. Если увеличить температуру магнетика, то при высокой t магнетик теряет свои свойства. Антиферромагнетики – вещества, в которых собственные магнитные моменты электрических свойств самопроизвольно ориентированы пропорционально друг другу в результате антиферромагнетика обладает крайне малой магнитной восприимчивостью и ведут себя как очень слабые парамагнетики. Ферромагнетики – вещества, у которых магнитный момент хотя и параллельны друг другу, но не скомпенсированы.

1)При внесении незаряженного проводника в эл. поле носители заряда приходят в движение :+ в направлении вектора Е, - в противоположную сторону. В результате у концов проводника возникнут заряды противоположного знака, называемого индуцированными. Поле этих зарядов направлено противоположно внешнему полю => накапливание зарядов у концов проводника приводит к ослабеванию в нём поля. Перераспределение носителей заряда происходит до тех пор, пока не будут выполнены условия равновесия зарядов в проводнике.1)Напряженность поля внутри проводника должно быть равно 0 Е=0 (φ=const). 2)Напряженность поля на поверхности проводника должна быть направлена по нормали к поверхности Е=Еn. Нейтральный проводник, внесенный в электрическое поле разрывает части линий напряженности. они заканчиваются на отрицательно индуцированных зарядах и вновь начинаются на +. Индуцированные заряды распределяются во внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее равно 0. На этом основывается электростатическая защита. 2)Фарадей предположил, что не только ток является причиной возникновения м. п., но и магнитное поле может являться причиной возникновения электрического поля. При приближении или удалении к контуру магнита или другого контура с током в первом появится ток. В момент внешнего отклонения ключа появляется импульс тока. Замкнув ключ и перемещая заряды меняется ток и в Ш контуре возникает ток. Фарадей выяснил, что ток в первом контуре возникает при всяком изменении магнитного потока, пронизывающего замкнутый контур. Такой ток называется индукционным, а явление возникновения индукционного тока при изменении магнитного потока через контур, ограничивающего этот поток называется электромагнитной индукцией. Фарадей обнаружил. что индуцированный ток определяется скоростью изменения магнитного потока dФ/dt, где dФ=BndS. Ленц установил правило, определяющее направление индукционного тока, согласно которому индукционный ток направлен так, чтобы препятствовать причине его возникновение вызывающей: При всяком изменении магнитного потока сквозь контур, ограничивающий это поток, возник индукционный ток такого направления, что его м.п., противоположно м.п. вызвавшему этот ток. ,ε_i=-dФ/dt. Электрический ток, текущий в замкнутом контуре, создает вокруг себя м.п., индукция которого по закону Био-Савара-Лапласа Ф~В,В~I => Ф~I=>Ф=LI. L-индуктивность (Гн). Если ток в контуре 1 Н, то индуктивность численно равна магнитному потоку, пронизывающему этот контур. Индуктивность зависит от размеров и формы контура, тех магнетических свойств среды, в которой расположен контур. Рассмотрим бесконечно длинный соленоид. Н=nI – напряженность поля на оси соленоида, n – число витков на единицу длины. B=μμ₀H= μμ₀nI; Ψ=ФN (Ψ- потокосцепление) N=nl – полное число витков. Ψ=BSN= μμ₀nISnl=> L=μμ₀n²IS= μμ₀n²V

3)Дано E Е₀/ε, D=ε₀εE, D=Eε₀+P => δ'=P=ε₀ (ε-1)E₀/ε=5,31 нКл/м²

Е₀=700% ω= ε₀εE²Sd/2= ε₀E₀²Sd/2ε=9,29 ГДж