Потенциал и разность потенциалов электростатического поля бесконечной равномерно заряженной цилиндрической поверхности (нити)

Бесконечный цилиндр радиуса R (рис. 131) заряжен равномерно с линейной плотностью t (t=dQ/dt — заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность -2prlЕ. По теореме Гаусса (81.2), при r>R 2prlE = tl/e0, откуда

Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E=0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует.

23. Проводники в электростатическом поле. Электроемкость проводника.

Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю: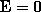

Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющей Е заряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместяться только на поверхности проводника. Это вытекает непосредственно из теоремы Гаусса, согласно которой заряд Q, который находится внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

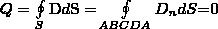
поскольку во всех точках внутри замкнутой поверхности D=0.

Теперь мы будем искать взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности σ . Для этого используем теорему Гаусса для бесконечно малого цилиндра с основаниями ΔS, который пересекает границу проводник—диэлектрик. Ось цилиндра направлена вдоль вектора Е (рис. 1). Поток вектора электрического смещения через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводника Е1 (а следовательно, и D1) есть нуль, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Используя теорему Гаусса, этот поток (DΔS) равен сумме зарядов (Q=σΔS), находящихся внутри поверхности: DΔS=σΔS т.е.

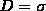(1)

или

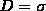(2)

где ε — диэлектрическая проницаемость среды, находящаяся вокруг проводника.

Значит, напряженность электростатического поля у поверхности проводника задается поверхностной плотностью зарядов. Можно показать, что формула (2) задает напряженность электростатического поля вблизи поверхности проводника абсолютно произвольной формы.

Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю. Если проводнику, уже несущему заряд q , сообщить еще заряд той же величины, то второй заряд должен распределиться по проводнику точно также, как и первый, в противном случае он создает в проводнике поле, не равное нулю. Таким образом, различные по величине заряды распределяются на удаленном от других тел (уединенном) проводнике подобным образом, т.е. отношение плотностей заряда в двух произвольных точках поверхности проводника при любой величине заряда будет одно и то же.

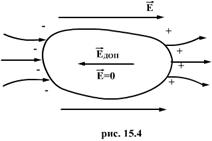
Отсюда вытекает, что потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в тоже число раз напряженности поля в каждой точке окружающего проводника пространства, т.е.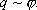

Вводя соответствующий коэффициент пропорциональности, запишем 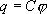или

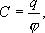
где С - называется электроемкостью.

Таким образом, электроемкость проводника есть физическая величина численно равная величине заряда, который необходимо сообщить данному проводнику для увеличения его потенциала на единицу. В СИ единицей емкости является Фарад (Ф).

Определим электроемкость уединенного шара. Потенциал заряженного шара радиуса R

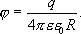
Сравнивая с 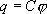получаем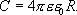

24. Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля.

1. Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q1 и Q2, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):

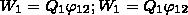
где φ12 и φ21 — соответственно потенциалы, которые создаются зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно, 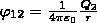и

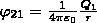
поэтому W1 = W2 = W и

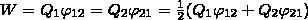
Добавляя к нашей системе из двух зарядов последовательно заряды Q3, Q4, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

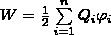(1)

где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го.

2. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна 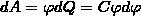");?>" alt="элементарная работа сил электрического поля заряженного проводника">

Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу

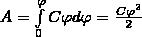(2)

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

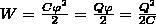(3)

Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем

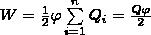
где Q=∑Qi - заряд проводника.

3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна

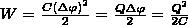(4)

где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.

Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда

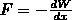(5)

Подставив в (4) выражение для емкости плоского конденсатора, получим

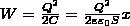(6)

Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:

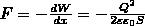
где знак минус указывает, что сила F является силой притяжения.

4. Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, используя выражением для емкости плоского конденсатора (C=ε0εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда

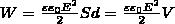(7)

где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.

Объемная плотность энергии электростатического поля (энергия единицы объема)

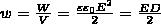(8)

Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε0Е.

Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.

25. Диэлектрики в электростатическом поле. Поляризация диэлектриков. Диэлектрическая проницаемость среды.

Два вида диэлектриков.Существующие диэлектрики можно разбить на два вида:

полярные, состоящие из таких молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают;

неполярные, состоящие из атомов или молекул, у которых центры распределения положительных и отрицательных зарядов совпадают. Следовательно, молекулы у этих диэлектриков разные.

К полярным диэлектрикам относятся спирты, вода и другие вещества; к неполярным - инертные газы, кислород, водород, бензол, полиэтилен и др.

. Они различаются строением молекул.

В зависимости от строения молекул (атомов) диэлектрика различается три типа поляризации:

а) ориентационная поляризация в полярных диэлектриках. Внешнее электрическое поле стремится ориентировать дипольные моменты жестких диполей вдоль направления электрического поля. Этому препятствует хаотическое тепловое движение молекул, стремящееся произвольно «разбросать» диполи. В итоге совместного действия поля и теплового движения возникает преимущественная ориентация дипольных электрических моментов вдоль поля, возрастающая с увеличением напряженности электрического поля и с уменьшением температуры;

б) электронная (деформационная) поляризация в неполярных диэлектриках. Под действием внешнего электрического поля в молекулах диэлектриков этого типа наводятся индуцированные дипольные моменты, направленные вдоль поля. Тепловое движение молекул не оказывает влияния на электронную поляризацию. В газообразных и жидких диэлектриках практически одновременно с ориентационной происходит и электронная поляризация.

в) ионная поляризация в твердых диэлектриках, имеющих ионные кристаллические решетки. Например, NaCl, CsCl и др. Внешнее электрическое поле вызывает смещения всех положительных ионов в направлении напряженности E, а всех отрицательных ионов - в противоположную сторону.

Диэлектрическая проницаемость (диэлектрическая постоянная) среды ε - безразмерная величина, характеризующая изолирующие свойства среды. Она показывает, во сколько раз взаимодействие между зарядами в однородной среде меньше, чем в вакууме. Диэлектрическая проницаемость воздуха близка к диэлектрической постоянной вакуума ε0, т.е. к единице. Диэлектрическая постоянная воды достаточно высока - около 80.

26. Вектор электростатической индукции. Теорема Остроградского-Гауса для электростатического поля в диэлектрике.

Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Напряженность электростатического поля, как следует из ранее полученной формулы E=E0/ε , зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна ε. Вектор напряженности Е, при переходе через границу диэлектриков, испытывает скачкообразное изменение, тем самым делая неудобства при расчетах электростатических полей. Поэтому необходимо помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен

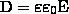(1)

Поскольку ε=1+θ и P=θε0E , вектор электрического смещения равен

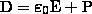(2)

Единица электрического смещения — кулон на метр в квадрате (Кл/м2).

Выясним, с чем можно связать вектор электрического смещения. Связанные заряды образуются в диэлектрике при наличии внешнего электростатического поля, который создается системой свободных электрических зарядов, т. е. в диэлектрике электростатическое поле свободных зарядов суммируется с дополнительным полем связанных зарядов. Результирующее поле в диэлектрике характеризуется вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D характеризуется электростатическое поле, которое создавается свободными зарядами. Связанные заряды, которые возникают в диэлектрике, могут вызвать перераспределение свободных зарядов, которые создают поле. Поэтому вектор D характеризует электростатическое поле, которое создается свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогичным образом, как и поле Е, поле D следует графически изображать с помощью линий электрического смещения, направление и густота которых задаются также, как и для линий напряженности.

Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Для любой замкнутой поверхности S поток вектора D сквозь эту поверхность

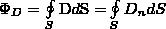
где Dn — проекция вектора D на единичный перпендикуляр n к площадке dS.

Теорема Гаусса для электростатического поля в диэлектрике:

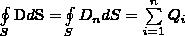(3)

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума Dn = ε0En (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен

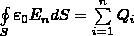
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как

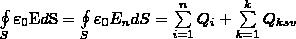
где ∑Qi и ∑Qsv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения.

27. Электростатический ток. Сила тока. Вектор плоскости (плотности) тока.

Электрическим током называется направленное (упорядоченное) движение заряженных частиц.

Электрический ток в проводниках различного рода представляет собой либо направленное движение электронов в металлах (проводники первого рода), имеющих отрицательный заряд, либо направленное движение более крупных частиц вещества — ионов, имеющих как положительный, так и отрицательный заряд — в электролитах (проводники второго рода), либо направленное движение электронов и ионов обоих знаков в ионизированных газах (проводники третьего рода).

За направление электрического тока условно принято направление движения положительно заряженных частиц.

Для существования электрического тока в веществе необходимо:

наличие заряженных частиц, способных свободно перемещаться по проводнику под действием сил электрического поля;

наличие источника тока, создающего и поддерживающего в проводнике в течение длительного времени электрическое поле.

Количественными характеристиками электрического тока являются сила тока I и плотность тока j.

Сила тока — скалярная физическая величина, определяемая отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку времени.

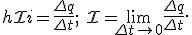
Единицей силы тока в СИ является ампер (А).

Если сила тока и его направление со временем не изменяются, то ток называется постоянным.

Единица силы тока — основная единица в СИ 1 А — есть сила такого неизменяющегося тока, который, проходя по двум бесконечно длинным параллельным прямолинейным проводникам очень маленького сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает силу взаимодействия между ними 2·10(7) Η на каждый метр длины проводников.

Рассмотрим, как зависит сила тока от скорости упорядоченного движения свободных зарядов.

Выделим участок проводника площадью сечения S и длиной Δl (рис. 1). Заряд каждой частицы q0. В объеме проводника, ограниченном сечениями 1 и 2, содержится nSΔl частиц, где n — концентрация частиц. Их общий заряд .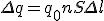

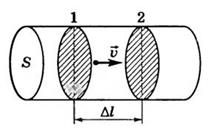Рис. 1

Если средняя скорость упорядоченного движения свободных зарядов 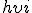, то за промежуток времени 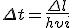все частицы, заключенные в рассматриваемом объеме, пройдут через сечение 2. Поэтому сила тока:

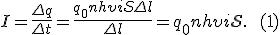
Таким образом, сила тока в проводнике зависит от заряда, переносимого одной частицей, их концентрации, средней скорости направленного движения частиц и площади поперечного сечения проводника.

Заметим, что в металлах модуль вектора средней скорости упорядоченного движения электронов при максимально допустимых значениях силы тока ~ 10-4 м/с, в то время как средняя скорость их теплового движения ~ 106 м/с.

Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е.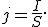

В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Как следует из формулы (1) 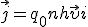, . Направление вектора плотности тока 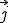совпадает с направлением вектора скорости упорядоченного движения 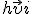положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.

28. Источник тока. Разность потенциалов, напряжение, электродвижущая сила (ЭДС).

Источник тока - это устройство, в котором происходит преобразование какого-либо вида энергии в электрическую энергию.

В любом источнике тока совершается работа по разделению положительно и отрицательно заряженных частиц, которые накапливаются на полюсах источника.

Существуют различные виды источников тока: Механический, тепловой, световой, химичесий.