Контрольная работа № 8 (2 часа)
А.Г.Мордкович, В.И.Глизбург (Москва)
Контрольные работы по алгебре
И началам математического анализа
Класс (базовый уровень)
В статье содержатся по два варианта контрольных работ по курсу «Алгебра и начала математического анализа 10-11 (базовый уровень)», ориентированных на учеб- ный комплект, готовящийся к публикации к началу 2008/09 уч. года издательством «Мнемозина» и включенный в Федеральный перечень учебников с грифом «Рекомен- довано»:
А.Г.Мордкович. Алгебра и начала математического анализа 10-11 (базовый уровень), часть 1. Учебник.
А.Г.Мордкович и др.Алгебра и начала математического анализа10-11 (базовый уровень), часть 2. Задачник.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания условно говоря базового, среднего (обязательного) уровня – до первой черты, задания уровня выше среднего – между первой и второй чертой, задания повышенной сложности – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий только до первой черты – оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) – оценка 4; ха успешное выполнение заданий всех трех уровней – оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Тематическое планирование было опубликовано в журнале «Математика в школе» ……..
Класс
Контрольная работа № 1
Вариант 1
1. Задает ли указанное правило функцию 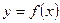 :
:
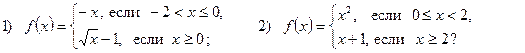
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 1, 3, – 1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию 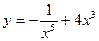 на четность.
на четность.
3. На числовой окружности взяты точки 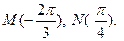 Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
4. Задайте аналитически и постройте график функции 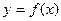 , у которой
, у которой
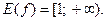
______________________________________________________________
5. Найдите функцию, обратную функции 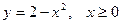 . Постройте
. Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
6. Известно, что функция 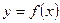 убывает на R. Решите неравенство
убывает на R. Решите неравенство
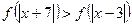 .
.
Вариант 2
1. Задает ли указанное правило функцию 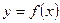 :
:
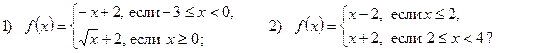
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 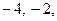 0, 4;
0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию 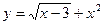 на четность.
на четность.
3. На числовой окружности взяты точки 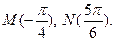 Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
4. Задайте аналитически и постройте график функции 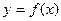 , у которой
, у которой
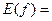
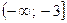 .
.
______________________________________________________________
5. Найдите функцию, обратную функции 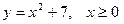 . Постройте
. Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
6.Известно, что функция 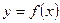 возрастает на R. Решите неравенство
возрастает на R. Решите неравенство
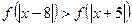 .
.
Контрольная работа № 2
Вариант 1
1. Вычислите: а) 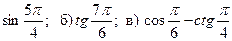 ;
;
г) 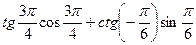 ; д)
; д) 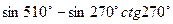 .
.
2. Упростите выражение 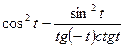 .
.
3. Решите уравнение: а) 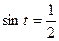 ; б)
; б) 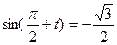 .
.
____________________________________________________________
4. Известно, что 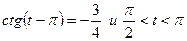 .
.
Найдите 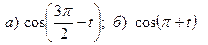 .
.
___________________________________
5. Расположите в порядке возрастания следующие числа:
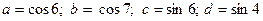 .
.
Вариант 2
1. Вычислите: а) 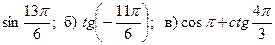 ;
;
г) 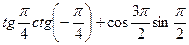 ; д)
; д) 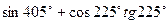 .
.
2. Упростите выражение 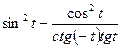 .
.
3. Решите уравнение: а) 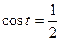 ; б)
; б) 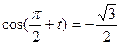 .
.
____________________________________________________________
4. Известно, что 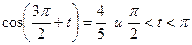 .
.
Найдите 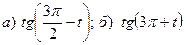 .
.
___________________________________
5. Расположите в порядке убывания следующие числа:
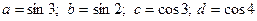 .
.
Контрольная работа № 3
Вариант 1
1. Не выполняя построения, установите, принадлежит ли графику функции 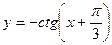 точка: а)
точка: а) 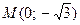 ; б) P
; б) P 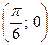 .
.
2. Исследуйте функцию на четность:
а) 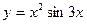 ; б)
; б) 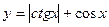 ; в)
; в) 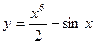 .
.
3. Исследуйте функцию 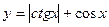 на периодичность; укажите
на периодичность; укажите
основной период, если он существует.
4. Решите графически уравнение 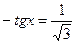 .
.
____________________________________________________________
5. Постройте график функции а) или б):
а) 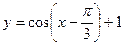 ; б)
; б) 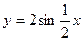 .
.
___________________________________
6. При каком значении параметра 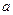 неравенство
неравенство 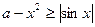
имеет единственное решение? Найдите это решение.
Вариант 2
1. Не выполняя построения, установите, принадлежит ли графику функции 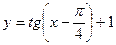 точка: а) M
точка: а) M 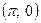 ; б) P
; б) P 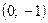 .
.
2. Исследуйте функцию на четность
а) 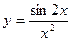 ; б)
; б) 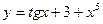 , в)
, в) 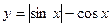 .
.
3. Исследуйте функцию 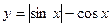 на периодичность; укажите
на периодичность; укажите
основной период, если он существует.
4. Решите графически уравнение 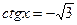 .
.
____________________________________________________________
5. Постройте график функции а) или б):
а) 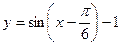 ; б)
; б) 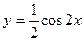 .
.
___________________________________
6. При каком значении параметра 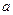 неравенство
неравенство 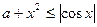
имеет единственное решение? Найдите это решение.
Контрольная работа № 4
Вариант 1
1. Вычислите: а) 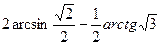 ; б)
; б) 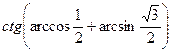 .
.
2. Решите уравнение: а) 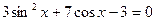 ; б)
; б) 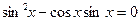 .
.
3. Найдите корни уравнения 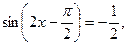 принадлежащие полуинтервалу
принадлежащие полуинтервалу 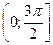 .
.
____________________________________________________________
4. Решите уравнение 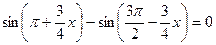 .
.
___________________________________
5. Решите уравнение 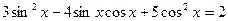 .
.
Вариант 2
1. Вычислите: а) 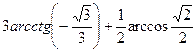 ; б)
; б) 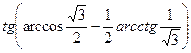 .
.
2. Решите уравнение: а) 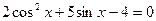 ; б)
; б) 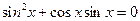 .
.
3. Найдите корни уравнения 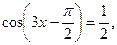 принадлежащие
принадлежащие
полуинтервалу 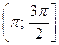 .
.
____________________________________________________________
4. Решите уравнение 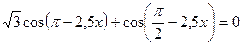 .
.
___________________________________
5. Решите уравнение 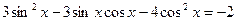 .
.
Контрольная работа № 5
Вариант 1
1. Вычислите: а) 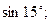 б)
б) 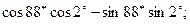
в) 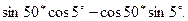
2. Упростите выражение 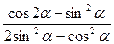 .
.
3. Решите уравнение 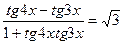 .
.
4. Найдите корни уравнения 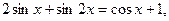 принадлежащие
принадлежащие
полуинтервалу 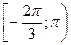 .
.
____________________________________________________________
5. Решите уравнение 
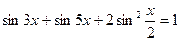 .
.
___________________________________
6. Докажите, что для любого x справедливо неравенство 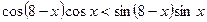 .
.
Вариант 2
1. Вычислите: а) 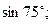 б)
б) 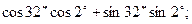
в) 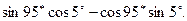
2. Упростите выражение 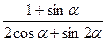 .
.
3. Решите уравнение 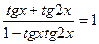 .
.
4. Найдите корни уравнения 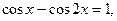 принадлежащие
принадлежащие
промежутку 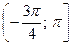 .
.
____________________________________________________________
5. Решите уравнение 
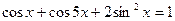 .
.
___________________________________
6. Докажите, что для любого x справедливо неравенство
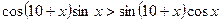 .
.
Контрольная работа № 6
Вариант 1
1. Вычислите первый, пятый и 100-й члены последовательности, если ее n-й член задается формулой 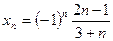 .
.
2. Представьте бесконечную периодическую десятичную дробь 1,(18)
в виде обыкновенной дроби.
3. Найдите производную функции: а) 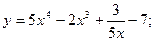
б) 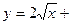
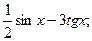 в)
в) 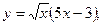 г)
г) 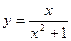 .
.
4. Найдите угловой коэффициент касательной к графику функции
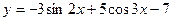 в точке с абсциссой
в точке с абсциссой 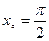 .
.
____________________________________________________________
5. Докажите, что функция 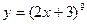 удовлетворяет соотношению
удовлетворяет соотношению
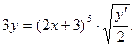
_________________________________
6. Найдите знаменатель бесконечно убывающей геометрической
прогрессии, у которой каждый член в 6 раз больше суммы всех ее последующих членов.
Вариант 2
1. Вычислите первый, седьмой и 200-й члены последовательности, если ее n-й член задается формулой 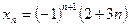 .
.
2. Представьте бесконечную периодическую десятичную дробь 2, (27)
в виде обыкновенной дроби.
3. Найдите производную функции: а) 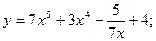
б) 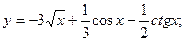 в)
в) 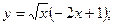 г)
г) 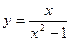 .
.
4. Найдите угловой коэффициент касательной к графику функции
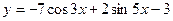 в точке с абсциссой
в точке с абсциссой 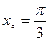 .
.
____________________________________________________________
5. Докажите, что функция 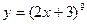 удовлетворяет соотношению
удовлетворяет соотношению
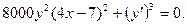
___________________________________
6. Сумма бесконечной геометрической прогрессии равна 4, а сумма
квадратов ее членов равна 48. Найдите первый член и знаменатель
прогрессии.
Контрольная работа № 7
Вариант 1
1. Составьте уравнение касательной к графику функции 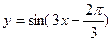
в точке 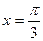
2. Составьте уравнения касательных к графику функции 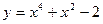
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
____________________________________________________________
3. Исследуйте функцию 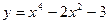 на монотонность и экстремумы и постройте ее график.
на монотонность и экстремумы и постройте ее график.
__________________________________
4. Найдите значение параметра 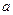 , при котором касательная к графику
, при котором касательная к графику
функции 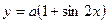 в точке с абсциссой
в точке с абсциссой 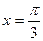 параллельна
параллельна
биссектрисе первой координатной четверти.
Вариант 2
1. Составьте уравнение касательной к графику функции 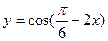
в точке 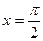
2. Составьте уравнения касательных к графику функции 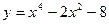
в точках его пересечения с осью абсцисс.
____________________________________________________________
3. Исследуйте функцию 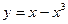 на монотонность и экстремумы
на монотонность и экстремумы
и постройте ее график.
___________________________________
4 Найдите значение параметра 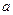 , при котором касательная к графику
, при котором касательная к графику
функции 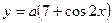 в точке с абсциссой
в точке с абсциссой 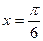 параллельна прямой
параллельна прямой
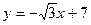 .
.
Контрольная работа № 8 (2 часа)
Вариант 1
1. Найдите наименьшее и наибольшее значения функции
а) 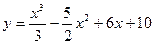 на отрезке
на отрезке 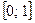 ;
;
б) 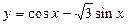 на отрезке
на отрезке 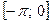 .
.
2. Найдите диагональ прямоугольника наибольшей площади,
вписанного в прямоугольный треугольник с катетами 18см и 24 см
и имеющего с ним общий прямой угол.
____________________________________________________________
3. Исследуйте функцию 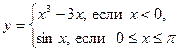 на монотонность
на монотонность
и экстремумы.
________________________________
4. При каких значениях параметра 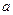 уравнение
уравнение 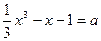 имеет три
имеет три
корня?
Вариант 2
1. Найдите наименьшее и наибольшее значения функции:
а) 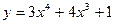 на отрезке
на отрезке 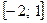 ;
;
б) 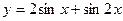 на отрезке
на отрезке 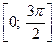 .
.
2. В прямоугольном треугольнике с катетами 36 и 48 на гипотенузе взята
точка. Из нее проведены прямые, параллельные катетам. Получился
прямоугольник, вписанный в данный треугольник. Где на гипотенузе
надо взять точку, чтобы площадь такого прямоугольника была
наибольшей?
____________________________________________________________
3. Исследуйте функцию 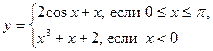 на монотонность
на монотонность
и экстремумы.
___________________________________
4. При каких значениях параметра 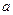 уравнение
уравнение 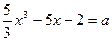 имеет два
имеет два
корня?
Класс
Контрольная работа № 1
Вариант 1
1. Вычислите: а) 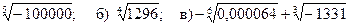 .
.
2. Расположите числа в порядке убывания: 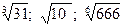 .
.
3. Постройте график функции: а) 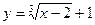 ; б)
; б) 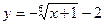 .
.
4. Вычислите: 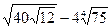 .
.
__________________________________________________________________
5. Найдите значение выражения 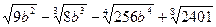 при
при
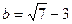 .
.
6. Решите уравнение 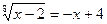 .
.
Вариант 2
1. Вычислите: а) 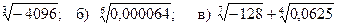 .
.
2. Расположите числа в порядке возрастания: 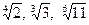 .
.
3. Постройте график функции: а) 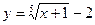 ; б)
; б) 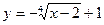 .
.
4. Вычислите: 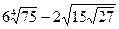 .
.
______________________________________________________________
5. Найдите значение выражения 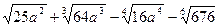 при
при 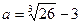 .
.
___________________________________
6. Решите уравнение 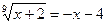 .
.
Контрольная работа № 2
Вариант 1
1. Вычислите: а) 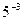 ; б)
; б) 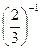 ; в)
; в) 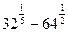 ; г)
; г) 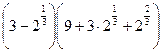 .
.
2. Постройте график функции: а) 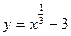 ; б)
; б) 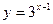 .
.
3. Решите уравнение: а) 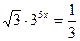 ; б)
; б) 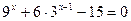 .
.
4. Решите неравенство 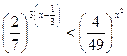 .
.
5. Составьте уравнение касательной к графику функции 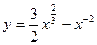
в точке 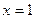 .
.
__________________________________________________________________
6. Найдите наибольшее и наименьшее значения функции 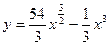
на отрезке 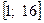 .
.
7. Дана функция 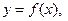 где
где 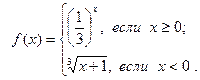
а) Вычислите 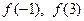 ; б) постройте график функции;
; б) постройте график функции;
в) найдите область значений функции;
г) выясните, при каких значениях параметра 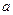 уравнение
уравнение 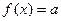
имеет два корня.
Вариант 2
1. Вычислите: а) 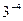 ; б)
; б) 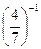 ; в)
; в) 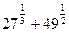 ; г)
; г) 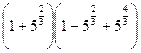 .
.
2. Постройте график функции: а) 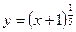 ; б)
; б) 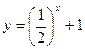 .
.
3. Решите уравнение: а) 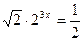 ; б)
; б) 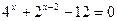 .
.
4. Решите неравенство 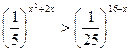 .
.
5. Составьте уравнение касательной к графику функции 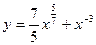
в точке 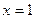 .
.
__________________________________________________________________
6. Найдите наибольшее и наименьшее значения функции 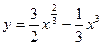
на отрезке 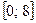 .
.
7. Дана функция 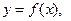 где
где 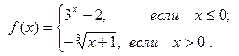
а) Вычислите 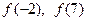 ; б) постройте график функции;
; б) постройте график функции;
в) найдите область значений функции; г) выясните, при каких значениях параметра 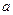 уравнение
уравнение 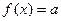 имеет два корня.
имеет два корня.
Контрольная работа № 3
Вариант 1
1. Вычислите: а) 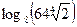 ; б)
; б) 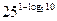 .
.
2. Постройте график функции: а) 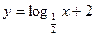 ; б)
; б) 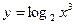 .
.
3. Решите уравнение: а) 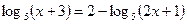 ; б)
; б) 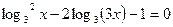 .
.
____________________________________________________________
4. Решите неравенство 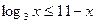 .
.
___________________________________
5. Решите уравнение 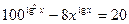 .
.
Вариант 2
1. Вычислите: а) 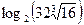 ; б)
; б) 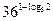 .
.
2. Постройте график функции: а) 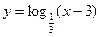 ; б)
; б) 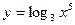 .
.
3. Решите уравнение: а) 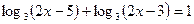 ; б)
; б) 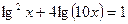 .
.
____________________________________________________________
4. Решите неравенство 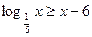 .
.
___________________________________
5. Решите уравнение 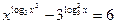 .
.
Контрольная работа № 4
Вариант 1
1. Решите неравенство 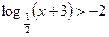 .
.
2. Исследуйте функцию 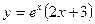 на монотонность и экстремумы.
на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции 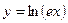 в точке
в точке 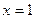 .
.
____________________________________________________________
4. Решите уравнение 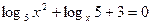 .
.
___________________________________
5. Решите систему уравнений 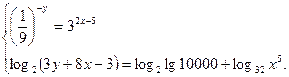
Вариант 2
1. Решите неравенство 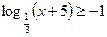 .
.
2. Исследуйте функцию 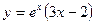 на монотонность и экстремумы.
на монотонность и экстремумы.
3. Напишите уравнение касательной к графику функции 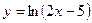
в точке 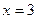 .
.
____________________________________________________________
4. Решите уравнение 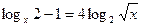 .
.
___________________________________
5. Решите систему уравнений 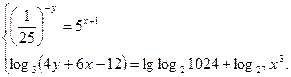
Контрольная работа № 5
Вариант 1
1. Докажите, что функция 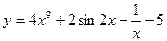 является первообразной для
является первообразной для
функции 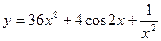 .
.
2. Для данной функции 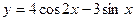 найдите ту первообразную, график
найдите ту первообразную, график
которой проходит через заданную точку 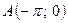 .
.
3. Вычислите интеграл: а) 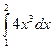 ; б)
; б) 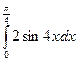 .
.
_________________________________________________________________
4. Вычислите площадь фигуры, ограниченной линиями
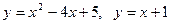 .
.
5. Известно, что функция 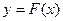 - первообразная для функции
- первообразная для функции
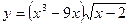 . Исследуйте функцию
. Исследуйте функцию 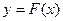 на монотонность
на монотонность
и экстремумы.
Вариант 2
1. Докажите, что функция 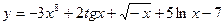 является
является
первообразной для функции 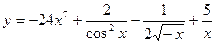 .
.
2. Для данной функции 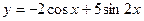 найдите ту первообразную,
найдите ту первообразную,
график которой проходит через заданную точку 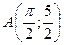 .
.
3. Вычислите интеграл: а) 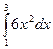 ; б)
; б) 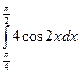 .
.
__________________________________________________________________
4. Вычислите площадь фигуры, ограниченной линиями
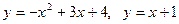 .
.
5. Известно, что функция 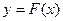 - первообразная для функции
- первообразная для функции
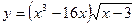 . Исследуйте функцию
. Исследуйте функцию 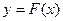 на монотонность
на монотонность
и экстремумы.
Контрольная работа № 6
Вариант 1
1. В клубе 25 спортсменов. Сколькими способами из них можно составить команду из четырех человек для участия
в четырехэтапной эстафете с учетом порядка пробега этапов?
2. Сколько трехзначных чисел можно составить из цифр 1,2,3,4,0 при условии, что каждая цифра может содержаться в записи числа лишь один раз?
3. Решите уравнение 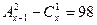 .
.
4. Напишите разложение степени бинома 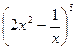 .
.
________________________________________________________
5. Из колоды в 36 карт вытаскивают две карты. Какова вероятность
извлечь при этом карты одинаковой масти?
6. На прямой взяты 6 точек, а на параллельной ей прямой – 7 точек.
Сколько существует треугольников, вершинами которых являются
данные точки?
Вариант 2
1. Сколькими способами можно составить трехцветный
полосатый флаг, если имеется материал пяти различных цветов?
2. Сколько различных трехзначных чисел можно составить из цифр 1,2,3
при условии, что цифры могут повторяться?
3. Решите уравнение 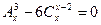 .
.
4. Напишите разложение степени бинома 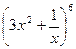 .
.
________________________________________________________
5. Из колоды в 36 карт вытаскивают три карты. Какова вероятность
того, что все они тузы?
6. Сколько существует треугольников, у которых вершины являются
вершинами данного выпуклого 10-угольника?
